
Statistische Variablentypen und Beispiele

Das statistische Variablen Sie sind Eigenschaften, die Menschen, Dinge oder Orte haben und die gemessen werden können. Beispiele für häufig verwendete Variablen sind Alter, Gewicht, Größe, Geschlecht, Familienstand, akademisches Niveau, Temperatur, die Anzahl der Stunden, die eine Glühbirne hält, und viele andere..
Eines der Ziele der Wissenschaft ist es, zu wissen, wie sich die Variablen eines Systems verhalten, um Vorhersagen über sein zukünftiges Verhalten zu treffen. Entsprechend ihrer Natur erfordert jede Variable eine spezifische Behandlung, um die maximale Information daraus zu erhalten..
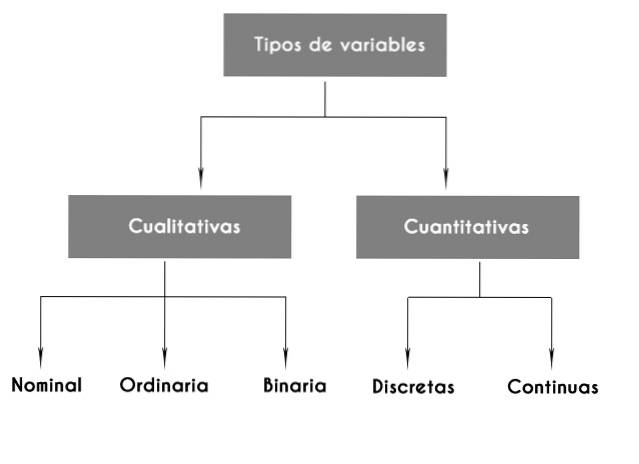
Die Anzahl der zu untersuchenden Variablen ist enorm, aber wenn wir die oben genannte Gruppe sorgfältig untersuchen, stellen wir sofort fest, dass einige numerisch ausgedrückt werden können, während andere dies nicht können..
Dies führt zu einer anfänglichen Klassifizierung statistischer Variablen in zwei grundlegende Typen: qualitative und numerische..
Artikelverzeichnis
- 1 Arten statistischer Variablen
- 1.1 - Qualitative Variablen
- 1.2 - Numerische oder quantitative Variablen
- 1.3 Diskrete Variablen
- 1.4 Kontinuierliche Variablen
- 1.5 - Abhängige und unabhängige Variablen
- 2 Referenzen
Arten statistischer Variablen
- Qualitative Variablen
Wie der Name schon sagt, werden qualitative Variablen verwendet, um Kategorien oder Qualitäten zu bezeichnen.
Ein bekanntes Beispiel für diese Art von Variablen ist der Familienstand: ledig, verheiratet, geschieden oder verwitwet. Keine dieser Kategorien ist größer als die andere, sie bezeichnet nur eine andere Situation.
Weitere Variablen dieses Typs sind:
-Akademischer Grad
-Monat des Jahres
-Marke des Autos, das gefahren wird
-Beruf
-Staatsangehörigkeit
-Länder, Städte, Bezirke, Landkreise und andere territoriale Abteilungen.
Eine Kategorie kann auch durch eine Nummer gekennzeichnet werden, z. B. die Telefonnummer, die Hausnummer, die Straße oder die Postleitzahl, ohne dass dies eine numerische Bewertung, sondern eine Bezeichnung darstellt.

Nominal-, Ordinal- und Binärvariablen
Die qualitativen Variablen können wiederum sein:
-Nominal, die der Qualität einen Namen zuweisen, wie zum Beispiel die Farbe.
-Ordnungszahlen, diese repräsentieren Ordnung, wie im Fall einer Skala von sozioökonomischen Schichten (hoch, mittel, niedrig) oder Meinungen über irgendeine Art von Vorschlag (zugunsten, gleichgültig, gegen). * *
-Binär, ruft auch an dichotom, Es gibt nur zwei mögliche Werte, wie z. B. Geschlecht. Dieser Variablen kann eine numerische Bezeichnung wie 1 und 2 zugewiesen werden, ohne dass eine numerische Auswertung oder eine beliebige Reihenfolge dargestellt wird.
* *Einige Autoren nehmen Ordnungsvariablen in die Gruppe der quantitativen Variablen auf, die nachstehend beschrieben werden. Es ist, weil sie Ordnung oder Hierarchie ausdrücken.
- Numerische oder quantitative Variablen
Diesen Variablen wird eine Nummer zugewiesen, da sie Größen wie Gehalt, Alter, Entfernungen und Noten darstellen, die in einer Prüfung erhalten wurden.
Sie werden häufig verwendet, um Präferenzen gegenüberzustellen und Trends abzuschätzen. Kann mit qualitativen Variablen verknüpft werden und Balkendiagramme und Histogramme erstellen, die die visuelle Analyse erleichtern.
Einige numerische Variablen können in qualitative Variablen umgewandelt werden, das Gegenteil ist jedoch nicht möglich. Beispielsweise kann die numerische Variable „Alter“ in Intervalle mit zugewiesenen Bezeichnungen unterteilt werden, z. B. Säuglinge, Kinder, Jugendliche, Erwachsene und ältere Menschen.
Es sollte jedoch beachtet werden, dass es Operationen gibt, die mit numerischen Variablen durchgeführt werden können, die offensichtlich nicht mit qualitativen Variablen ausgeführt werden können, beispielsweise die Berechnung von Durchschnittswerten und anderen statistischen Schätzern..
Wenn Sie Berechnungen durchführen möchten, müssen Sie die Variable "Alter" als numerische Variable beibehalten. Andere Anwendungen erfordern jedoch möglicherweise keine numerischen Details. Für diese Anwendungen würde es ausreichen, die genannten Bezeichnungen zu belassen.
Numerische Variablen werden wiederum in zwei große Kategorien unterteilt: diskrete Variablen und kontinuierliche Variablen..
Diskrete Variablen
Diskrete Variablen nehmen nur bestimmte Werte an und zeichnen sich dadurch aus, dass sie zählbar sind, beispielsweise die Anzahl der Kinder in einer Familie, die Anzahl der Haustiere, die Anzahl der Kunden, die täglich ein Geschäft besuchen, und Abonnenten eines Kabelunternehmens, um nur einige zu nennen Beispiele.
Wenn Sie beispielsweise die Variable "Anzahl der Haustiere" definieren, werden die Werte aus der Menge der natürlichen Zahlen abgeleitet. Eine Person kann 0, 1, 2, 3 oder mehr Haustiere haben, aber niemals 2,5 Haustiere.
Eine diskrete Variable hat jedoch notwendigerweise natürliche oder ganzzahlige Werte. Dezimalzahlen sind ebenfalls nützlich, da das Kriterium zur Bestimmung, ob eine Variable diskret ist, darin besteht, dass sie zählbar oder zählbar ist.
Angenommen, der Anteil defekter Glühbirnen in einer Fabrik, der zufällig aus einer Stichprobe von 50, 100 oder N Glühbirnen entnommen wird, ist als Variable definiert..
Wenn keine Glühbirnen defekt sind, nimmt die Variable den Wert 0 an. Wenn jedoch 1 von N Glühbirnen defekt ist, ist die Variable 1 / N, wenn zwei defekt sind, ist sie 2 / N usw. bis zu dem Fall, dass die N. Die Glühbirnen waren defekt und in diesem Fall wäre der Anteil 1.
Kontinuierliche Variablen
Im Gegensatz zu diskreten Variablen können kontinuierliche Variablen einen beliebigen Wert annehmen. Zum Beispiel das Gewicht der Schüler, die ein bestimmtes Fach belegen, Größe, Temperatur, Zeit, Länge und vieles mehr.
Da die stetige Variable unendliche Werte annimmt, können alle Arten von Berechnungen mit der gewünschten Genauigkeit durchgeführt werden, indem einfach die Anzahl der Dezimalstellen angepasst wird..
In der Praxis gibt es kontinuierliche Variablen, die als diskrete Variablen ausgedrückt werden können, beispielsweise das Alter einer Person.
Das genaue Alter einer Person kann in Jahren, Monaten, Wochen, Tagen und mehr gezählt werden, abhängig von der gewünschten Präzision. Es wird jedoch normalerweise in Jahren gerundet und wird daher diskret.
Das Einkommen einer Person ist ebenfalls eine kontinuierliche Variable, aber es ist normalerweise besser, wenn Intervalle festgelegt werden.
- Abhängige und unabhängige Variablen
Die abhängigen Variablen sind diejenigen, die während eines Experiments gemessen werden, um die Beziehung zu anderen zu untersuchen, die als unabhängige Variablen betrachtet werden.
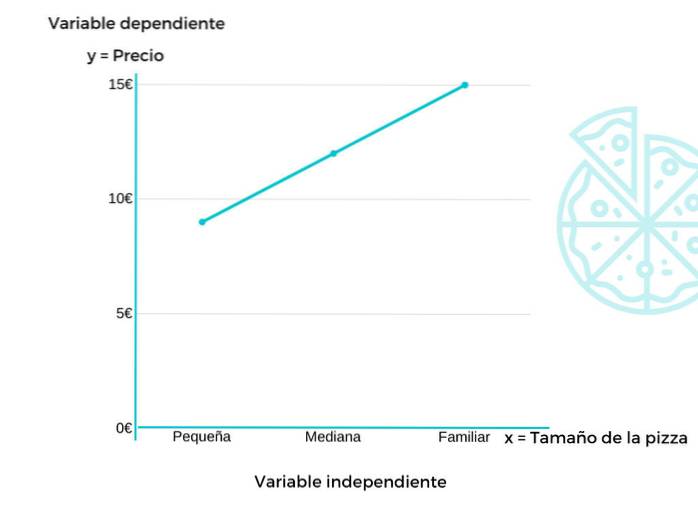
Beispiel 1
In diesem Beispiel sehen wir die Preisentwicklung der Pizzen eines Lebensmittelunternehmens in Abhängigkeit von ihrer Größe.
Die abhängige Variable (y) wäre der Preis, während die unabhängige Variable (x) die Größe wäre. In diesem Fall kostet die kleine Pizza 9 €, die mittlere 12 € und die Familienpizza 15 €.
Das heißt, wenn die Größe der Pizza zunimmt, kostet sie mehr. Daher wäre der Preis von der Größe abhängig.
Diese Funktion wäre y = f (x)
Beispiel 2
Ein einfaches Beispiel: Wir wollen den Effekt untersuchen, der durch Änderungen des Stroms I durch einen Metalldraht erzeugt wird, für den die Spannung V zwischen den Enden dieses Drahtes gemessen wird.
Die unabhängige Variable (die Ursache) ist der Strom, während die abhängige Variable (die Wirkung) die Spannung ist, deren Wert vom Strom abhängt, der durch den Draht fließt..
Im Experiment soll gesucht werden, wie das Gesetz für V ist, wenn ich variiert werde. Wenn sich herausstellt, dass die Abhängigkeit der Spannung vom Strom linear ist, dh: V ∝ I, ist der Leiter ohmsch und die Proportionalitätskonstante ist der Widerstand des Drahtes.
Die Tatsache, dass eine Variable in einem Experiment unabhängig ist, bedeutet jedoch nicht, dass dies in einem anderen Experiment der Fall ist. Dies hängt vom untersuchten Phänomen und der Art der durchzuführenden Forschung ab..
Beispielsweise wird der Strom I, der durch einen geschlossenen Leiter fließt, der sich in einem konstanten Magnetfeld dreht, zur abhängigen Variablen in Bezug auf die Zeit t, die zur unabhängigen Variablen werden würde.
Verweise
- Berenson, M. 1985. Statistik für Management und Wirtschaft. Interamericana S.A..
- Canavos, G. 1988. Wahrscheinlichkeit und Statistik: Anwendungen und Methoden. Mcgraw Hügel.
- Devore, J. 2012. Wahrscheinlichkeit und Statistik für Ingenieurwesen und Wissenschaft. 8 .. Auflage. Engagieren.
- Wirtschaftsenzyklopädie. Kontinuierliche Variablen. Wiederhergestellt von: encyclopediaeconomica.com.
- Levin, R. 1988. Statistik für Administratoren. 2 .. Auflage. Prentice Halle.
- Walpole, R. 2007. Wahrscheinlichkeit und Statistik für Ingenieurwissenschaften und Naturwissenschaften. Pearson.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.