Gleichschenklige Dreieckseigenschaften, Formel und Fläche, Berechnung

EIN gleichschenkligen Dreiecks ist ein Polygon mit drei Seiten, von denen zwei das gleiche Maß und die dritte Seite ein anderes Maß haben. Diese letzte Seite wird Basis genannt. Aufgrund dieser Eigenschaft erhielt es diesen Namen, was auf Griechisch "gleiche Beine" bedeutet.

Dreiecke sind Polygone, die als die einfachsten in der Geometrie angesehen werden, da sie aus drei Seiten, drei Winkeln und drei Eckpunkten bestehen. Sie haben die geringste Anzahl von Seiten und Winkeln in Bezug auf die anderen Polygone, ihre Verwendung ist jedoch sehr umfangreich.

Artikelverzeichnis

• 1 Eigenschaften gleichschenkliger Dreiecke
  • 1.1 Komponenten
• 2 Eigenschaften
  • 2.1 Innenwinkel
  • 2.2 Summe der Seiten
  • 2.3 Kongruente Seiten
  • 2.4 Kongruente Winkel
  • 2.5 Höhe, Median, Halbierende und Halbierende fallen zusammen
  • 2.6 Relative Höhen
  • 2.7 Koinzidentes Orthozentrum, Barycenter, Incenter und Circumcenter
• 3 So berechnen Sie den Umfang?
• 4 So berechnen Sie die Höhe?
• 5 So berechnen Sie die Fläche?
• 6 So berechnen Sie die Basis des Dreiecks?
• 7 Übungen
  • 7.1 Erste Übung
  • 7.2 Zweite Übung
  • 7.3 Dritte Übung
• 8 Referenzen

Eigenschaften gleichschenkliger Dreiecke

Das gleichschenklige Dreieck wurde anhand des Maßes seiner Seiten als Parameter klassifiziert, da zwei seiner Seiten kongruent sind (sie haben die gleiche Länge)..

Aufgrund der Amplitude der Innenwinkel werden gleichschenklige Dreiecke wie folgt klassifiziert:

• Gleichschenkliges rechtwinkliges Dreieck: zwei seiner Seiten sind gleich. Einer seiner Winkel ist richtig (90^oder) und die anderen sind gleich (45^oder jeder)
• Gleichschenkliges stumpfes Dreieck: zwei seiner Seiten sind gleich. Einer seiner Winkel ist stumpf (> 90)^oder).
• Gleichschenkliges spitzes Dreieck: zwei seiner Seiten sind gleich. Alle seine Winkel sind spitz (< 90^oder), wobei zwei das gleiche Maß haben.

Komponenten (bearbeiten)

• Median: ist eine Linie, die vom Mittelpunkt einer Seite beginnt und den gegenüberliegenden Scheitelpunkt erreicht. Die drei Mediane laufen an einem Punkt zusammen, der als Schwerpunkt oder Schwerpunkt bezeichnet wird..
• Bisektor: ist ein Strahl, der den Winkel jedes Scheitelpunkts in zwei gleich große Winkel teilt. Deshalb ist es als Symmetrieachse bekannt und diese Art von Dreiecken hat nur eine.
• Die Mittlerin: ist ein Segment senkrecht zur Seite des Dreiecks, dessen Ursprung in der Mitte des Dreiecks liegt. Es gibt drei Mediatices in einem Dreieck, die sich an einem Punkt treffen, der als Umkreiszentrum bezeichnet wird.
• Die Höhe: ist die Linie, die vom Scheitelpunkt zur gegenüberliegenden Seite verläuft, und auch diese Linie verläuft senkrecht zu dieser Seite. Alle Dreiecke haben drei Höhen, die an einem Punkt zusammenfallen, der als Orthozentrum bezeichnet wird..

Eigenschaften

Gleichschenklige Dreiecke werden definiert oder identifiziert, weil sie mehrere Eigenschaften haben, die sie darstellen und aus den von großen Mathematikern vorgeschlagenen Theoremen stammen:

Innenwinkel

Die Summe der Innenwinkel beträgt immer 180^oder.

Summe der Seiten

Die Summe der Maße zweier Seiten muss immer größer sein als das Maß der dritten Seite, a + b> c.

Kongruente Seiten

Gleichschenklige Dreiecke haben zwei Seiten mit dem gleichen Maß oder der gleichen Länge. das heißt, sie sind kongruent und die dritte Seite unterscheidet sich von diesen.

Kongruente Winkel

Gleichschenklige Dreiecke werden auch als Isoangle-Dreiecke bezeichnet, da sie zwei Winkel haben, die das gleiche Maß haben (kongruent). Diese befinden sich an der Basis des Dreiecks gegenüber den gleich langen Seiten.

Aus diesem Grund wurde der Satz generiert, der besagt, dass:

"Wenn ein Dreieck zwei kongruente Seiten hat, sind auch die diesen Seiten gegenüberliegenden Winkel kongruent." Wenn ein Dreieck gleichschenklig ist, sind die Winkel seiner Basen daher kongruent.

Beispiel:

Die folgende Abbildung zeigt ein Dreieck ABC. Durch Ziehen seiner Winkelhalbierenden vom Scheitelpunkt des Winkels B zur Basis wird das Dreieck in zwei gleiche Dreiecke BDA und BDC unterteilt:

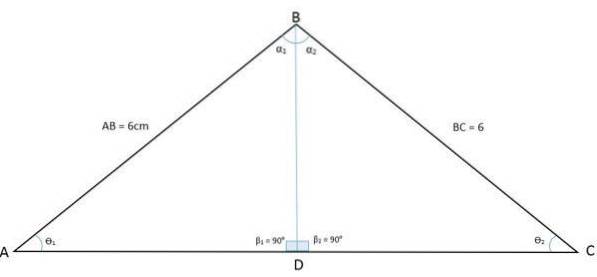
Auf diese Weise wurde auch der Winkel des Scheitelpunkts B in zwei gleiche Winkel geteilt. Die Halbierende ist jetzt die gemeinsame Seite (BD) zwischen diesen beiden neuen Dreiecken, während die Seiten AB und BC die kongruenten Seiten sind. Wir haben also den Fall der Kongruenzseite, des Winkels, der Seite (LAL).

Dies zeigt, dass die Winkel der Eckpunkte A und C das gleiche Maß haben, und es kann gezeigt werden, dass, da die Dreiecke BDA und BDC kongruent sind, auch die Seiten AD und DC kongruent sind..

Höhe, Median, Halbierende und Halbierende fallen zusammen

Die Linie, die vom Scheitelpunkt gegenüber der Basis zum Mittelpunkt der Basis des gleichschenkligen Dreiecks gezogen wird, ist gleichzeitig die Höhe, der Median und die Winkelhalbierende sowie die Winkelhalbierende relativ zum entgegengesetzten Winkel der Basis..

Alle diese Segmente fallen in einem zusammen, das sie darstellt.

Beispiel:

Die folgende Abbildung zeigt das Dreieck ABC mit einem Mittelpunkt M, der die Basis in zwei Segmente BM und CM unterteilt.

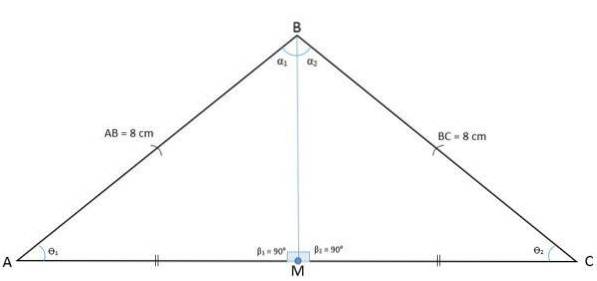
Durch Zeichnen eines Segments vom Punkt M zum gegenüberliegenden Scheitelpunkt wird per Definition der Median AM erhalten, der relativ zum Scheitelpunkt A und zur Seite BC ist.

Da das Segment AM das Dreieck ABC in zwei gleiche Dreiecke AMB und AMC unterteilt, bedeutet dies, dass der Fall der Kongruenzseite, des Winkels und der Seite vorliegt und daher AM auch die Halbierende von BÂC ist.

Daher ist die Winkelhalbierende immer gleich dem Median und umgekehrt..

Das Segment AM bildet Winkel, die für die Dreiecke AMB und AMC das gleiche Maß haben. das heißt, sie ergänzen sich so, dass das Maß jedes einzelnen sein wird:

Med. (AMB) + Med. (AMC) = 180^oder

zwei _{* *} Med. (AMC) = 180^oder

Med. (AMC) = 180^oder ÷ 2

Med. (AMC) = 90^oder

Es ist bekannt, dass die durch das Segment AM gebildeten Winkel in Bezug auf die Basis des Dreiecks richtig sind, was anzeigt, dass dieses Segment vollständig senkrecht zur Basis ist..

Stellt daher die Höhe und die Winkelhalbierende dar, in dem Wissen, dass M der Mittelpunkt ist.

Daher die Linie AM:

• Repräsentiert auf der Höhe von BC.
• Ist mittelgroß.
• Es ist in der Halbierenden von BC enthalten.
• Es ist die Winkelhalbierende des Scheitelpunktwinkels

Relative Höhen

Höhen, die relativ zu gleichen Seiten sind, haben ebenfalls das gleiche Maß.

Da das gleichschenklige Dreieck zwei gleiche Seiten hat, sind auch ihre beiden jeweiligen Höhen gleich..

Ortocenter, Barycenter, Incenter und koinzidentes Circumcenter

Da die Höhe, der Median, die Winkelhalbierende und die Winkelhalbierende relativ zur Basis gleichzeitig durch dasselbe Segment dargestellt werden, sind das Orthozentrum, das mittlere Barycenter und das Circumcenter kollineare Punkte, dh sie befinden sich auf derselben Linie:

So berechnen Sie den Umfang?

Der Umfang eines Polygons wird durch Hinzufügen der Seiten berechnet.

Da in diesem Fall das gleichschenklige Dreieck zwei Seiten mit demselben Maß hat, wird sein Umfang mit der folgenden Formel berechnet:

P = 2_{* *}(Seite a) + (Seite b).

Wie berechnet man die Höhe??

Die Höhe ist die Linie senkrecht zur Basis. Sie teilt das Dreieck in zwei gleiche Teile, wenn es sich zum gegenüberliegenden Scheitelpunkt erstreckt.

Die Höhe repräsentiert das gegenüberliegende Bein (a), die Mitte der Basis (b / 2) das benachbarte Bein und die Seite "a" repräsentiert die Hypotenuse.

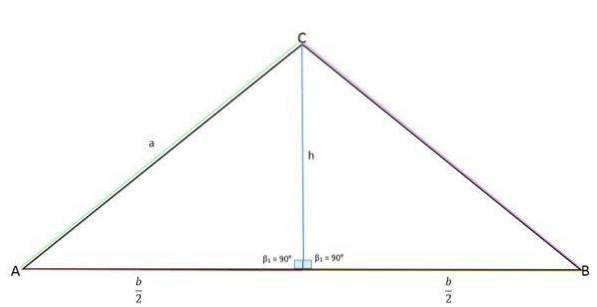
Mit dem Satz von Pythagoras kann der Wert der Höhe bestimmt werden:

zu^zwei + b^zwei = c^zwei

Wo:

zu^zwei = Höhe (h).

b^zwei = b / 2.

c^zwei = Seite a.

Wenn wir diese Werte in den Satz von Pythagoras einsetzen und nach der Höhe suchen, haben wir:

h^zwei + ((b / zwei)^zwei = zu^zwei

h^zwei + b^zwei / 4 = zu^zwei

h^zwei = zu^zwei - b^zwei / 4

h = √ (zu^zwei - b^zwei / 4).

Wenn der von den kongruenten Seiten gebildete Winkel bekannt ist, kann die Höhe mit der folgenden Formel berechnet werden:

Wie berechnet man die Fläche??

Die Fläche der Dreiecke wird immer mit derselben Formel berechnet, wobei die Basis mit der Höhe multipliziert und durch zwei geteilt wird:

Es gibt Fälle, in denen nur die Maße von zwei Seiten des Dreiecks und der zwischen ihnen gebildete Winkel bekannt sind. In diesem Fall müssen zur Bestimmung der Fläche die trigonometrischen Verhältnisse angewendet werden:

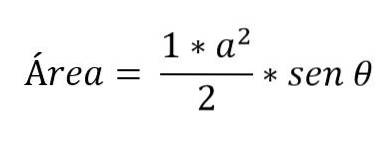
So berechnen Sie die Basis des Dreiecks?

Da das gleichschenklige Dreieck zwei gleiche Seiten hat, muss zur Bestimmung des Wertes seiner Basis mindestens das Maß der Höhe oder eines seiner Winkel bekannt sein.

In Kenntnis der Höhe wird der Satz von Pythagoras verwendet:

zu^zwei + b^zwei = c^zwei

Wo:

zu^zwei = Höhe (h).

c^zwei = Seite a.

b^zwei = b / 2 ist unbekannt.

Wir lösen für b^zwei der Formel und wir müssen:

b^zwei = a^zwei - c^zwei

b = √ a^zwei - c^zwei

Da dieser Wert der Hälfte der Basis entspricht, muss er mit zwei multipliziert werden, um das vollständige Maß für die Basis des gleichschenkligen Dreiecks zu erhalten:

b = 2 _{* *} (√ a^zwei - c^zwei)

Für den Fall, dass nur der Wert der gleichen Seiten und der Winkel zwischen ihnen bekannt sind, wird eine Trigonometrie angewendet, bei der eine Linie vom Scheitelpunkt zur Basis gezogen wird, die das gleichschenklige Dreieck in zwei rechtwinklige Dreiecke teilt.

Auf diese Weise wird die Hälfte der Basis berechnet mit:

Es ist auch möglich, dass nur der Wert der Höhe und des Winkels des Scheitelpunkts bekannt ist, der der Basis gegenüberliegt. In diesem Fall kann durch Trigonometrie die Basis bestimmt werden:

Ausbildung

Erste Übung

Finden Sie den Bereich des gleichschenkligen Dreiecks ABC, wobei Sie wissen, dass zwei seiner Seiten 10 cm und die dritte Seite 12 cm betragen.

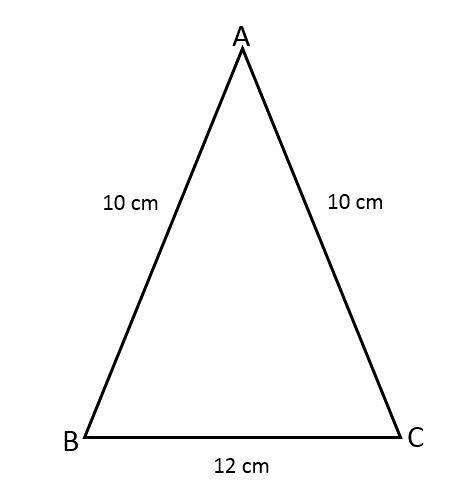
Lösung

Um die Fläche des Dreiecks zu finden, muss die Höhe unter Verwendung der Flächenformel berechnet werden, die sich auf den Satz von Pythagoras bezieht, da der Wert des Winkels zwischen den gleichen Seiten nicht bekannt ist.

Wir haben die folgenden Daten des gleichschenkligen Dreiecks:

• Gleiche Seiten (a) = 10 cm.
• Basis (b) = 12 cm.

Die Werte werden in der Formel ersetzt:

Zweite Übung

Die Länge der beiden gleichen Seiten eines gleichschenkligen Dreiecks beträgt 42 cm, die Vereinigung dieser Seiten bildet einen Winkel von 130 cm^oder. Bestimmen Sie den Wert der dritten Seite, die Fläche dieses Dreiecks und den Umfang.

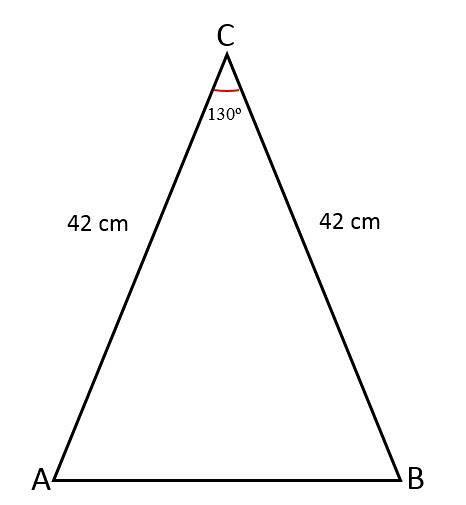
Lösung

In diesem Fall sind die Maße der Seiten und der Winkel zwischen ihnen bekannt..

Um den Wert der fehlenden Seite, dh der Basis dieses Dreiecks, zu kennen, wird eine dazu senkrechte Linie gezeichnet, die den Winkel in zwei gleiche Teile teilt, einen für jedes gebildete rechtwinklige Dreieck.

• Gleiche Seiten (a) = 42 cm.
• Winkel (Ɵ) = 130^oder

Nun wird durch Trigonometrie der Wert der Hälfte der Basis berechnet, der der Hälfte der Hypotenuse entspricht:

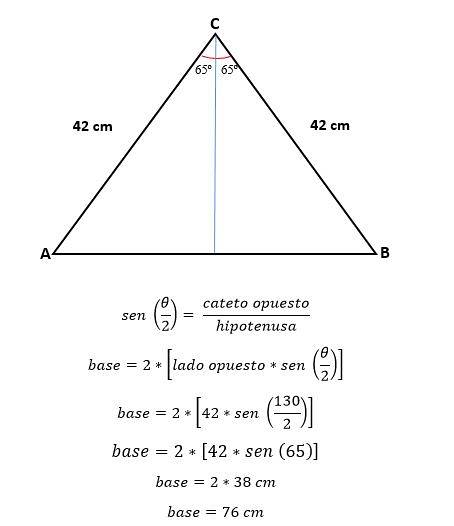
Um die Fläche zu berechnen, muss die Höhe dieses Dreiecks bekannt sein, die durch Trigonometrie oder nach dem Satz von Pythagoras berechnet werden kann, nachdem der Wert der Basis bereits bestimmt wurde.

Durch Trigonometrie wird es sein:

Der Umfang wird berechnet:

P = 2_{* *}(Seite a) + (Seite b).

P = 2_{* *} (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Dritte Übung

Berechnen Sie die Innenwinkel des gleichschenkligen Dreiecks, wobei Sie wissen, dass der Winkel der Basis = 55 beträgt^oder

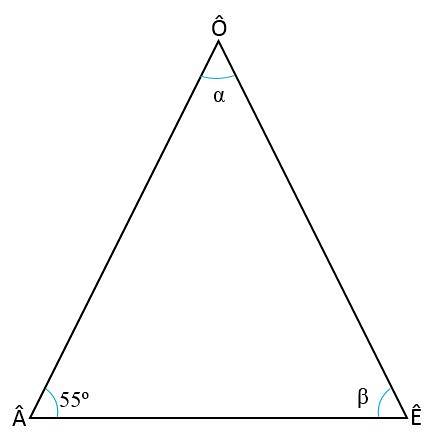
Lösung

Um die beiden fehlenden Winkel (Ê und Ô) zu finden, müssen zwei Eigenschaften von Dreiecken berücksichtigt werden:

• Die Summe der Innenwinkel jedes Dreiecks beträgt immer = 180^oder::

+ Ê + Ô = 180 ^oder

• In einem gleichschenkligen Dreieck sind die Winkel der Basis immer kongruent, dh sie haben das gleiche Maß, daher:

 = Ô

Ê = 55^oder

Um den Wert des Winkels Ê zu bestimmen, ersetzen wir die Werte der anderen Winkel in der ersten Regel und lösen nach Ê:

55^oder + 55^oder + Ô = 180 ^oder

110 ^oder + Ô = 180 ^oder

Ô = 180 ^oder - 110 ^oder

Ô = 70 ^oder.

Verweise

1. Álvarez, E. (2003). Elemente der Geometrie: mit zahlreichen Übungen und Geometrie des Kompasses. Universität von Medellin.
2. Álvaro Rendón, A. R. (2004). Technische Zeichnung: Aufgabenheft.
3. Angel, A. R. (2007). Elementare Algebra. Pearson Ausbildung.
4. Arthur Goodman, L. H. (1996). Algebra und Trigonometrie mit analytischer Geometrie. Pearson Ausbildung.
5. Baldor, A. (1941). Algebra. Havanna: Kultur.
6. José Jiménez, L. J. (2006). Mathe 2.
7. Tuma, J. (1998). Handbuch für Technische Mathematik. Wolfram MathWorld.