
Diskrete Fourier-Transformationseigenschaften, Anwendungen, Beispiele
Das diskrete Fourier-Transformation ist eine numerische Methode, mit der Abtastwerte definiert werden, die sich auf die Spektralfrequenzen beziehen, aus denen ein Signal besteht. Untersuchen Sie periodische Funktionen in geschlossenen Parametern und erhalten Sie ein weiteres diskretes Signal.
Um die diskrete Fourier-Transformation von N Punkten auf einem diskreten Signal zu erhalten, müssen die folgenden 2 Bedingungen für eine Sequenz erfüllt sein x [n]
x [n] = 0 n < 0 ˄ n > N - 1
Wenn diese Bedingungen erfüllt sind, kann die diskrete Fourier-Transformation definiert werden als
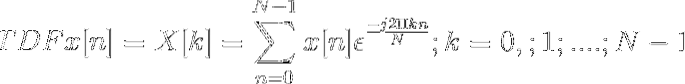
Die diskrete Fourier-Transformation kann als N-Punkt-Abtastung der Fourier-Transformation definiert werden.
Artikelverzeichnis
- 1 Interpretation der diskreten Fourier-Transformation
- 2 Eigenschaften
- 2.1 Linearität
- 2.2 Dualität
- 2.3 Faltung
- 2.4 Scrollen
- 2.5 Symmetrie konjugieren
- 2.6 Modulation
- 2.7 Produkt
- 2.8 Symmetrie
- 2.9 Konjugieren
- 2.10 Parseval-Gleichung
- 3 Ähnlichkeiten und Unterschiede zur Fourier-Transformation
- 4 Wofür ist die diskrete Fourier-Transformation??
- 5 Geschichte
- 6 Diskrete Fourier-Transformation und ihre Umkehrung
- 7 Geflügelt
- 8 Anwendungen
- 8.1 Berechnung der Grundlösung
- 8.2 Signaltheorie
- 9 Die Fourier-Reihe
- 10 Andere Formen der Fourier-Reihe
- 11 Beispiele
- 12 Übungen
- 12.1 Übung 1
- 12.2 Übung 2
- 13 Referenzen
Interpretation der diskreten Fourier-Transformation

Es gibt zwei Gesichtspunkte, aus denen die mit einer Sequenz x erhaltenen Ergebnisse interpretiert werden könnens[n] durch die diskrete Fourier-Transformation.
-Der erste entspricht den Spektralkoeffizienten, die bereits aus der Fourier-Reihe bekannt sind. Es wird in diskreten periodischen Signalen beobachtet, wobei Abtastwerte mit der Sequenz x übereinstimmens[n].
-Die zweite befasst sich mit dem Spektrum eines diskreten aperiodischen Signals mit Abtastwerten, die der Sequenz x entsprechens[n].
Die diskrete Transformation ist eine Annäherung an das Spektrum des ursprünglichen analogen Signals. Seine Phase hängt von den Abtastzeitpunkten ab, während seine Größe vom Abtastintervall abhängt..
Eigenschaften
Die algebraischen Grundlagen der Struktur bilden die logischen Grundlagen der folgenden Abschnitte.
Linearität
C. S.n → C. F [S.k]; Wenn eine Sequenz mit einem Skalar multipliziert wird, ist dies auch ihre Transformation.
T.n + V.n = F [T.k] + F [V.k]; Die Transformation einer Summe ist gleich der Summe der Transformationen.
Dualität
F [S.n] → (1 / N) S.-k; Wenn die diskrete Fourier-Transformation in einen bereits transformierten Ausdruck umgerechnet wird, wird derselbe Ausdruck erhalten, in N skaliert und in Bezug auf die vertikale Achse invertiert.
Faltung
Bei ähnlichen Zielen wie bei der Laplace-Transformation bezieht sich die Faltung von Funktionen auf das Produkt zwischen ihren Fourier-Transformationen. Faltung gilt auch für diskrete Zeiten und ist für viele moderne Verfahren verantwortlich..
X.n * R.n → F [X.n] .F [R.n]; Die Transformation einer Faltung ist gleich dem Produkt der Transformationen.
X.n . R.n→ F [X.n] * F [R.n]; Die Transformation eines Produkts ist gleich der Faltung der Transformationen.
Verschiebung
X.n-m → F [X.k] e -i (2π / N) km ;; Wenn eine Sequenz in m Abtastwerten verzögert ist, ist ihre Auswirkung auf die diskrete Transformation eine Modifikation des durch (2π / N) km definierten Winkels.
Symmetrie konjugiert
X.t [-k] = X *t[k] = X.t [N - K]
Modulation
W.-nmN. . x [n] ↔ X.t[k - m]
Produkt
x [n] y [n] ↔ (1 / N) X.t[k] * Y.t[k]
Symmetrie
X [-n] ↔ X.t[-k] = X *t[k]
Konjugieren
x * [n] ↔ X *t[-k]
Parseval-Gleichung
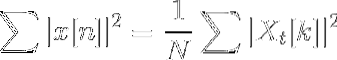
Ähnlichkeiten und Unterschiede mit der Fourier-Transformation
In Bezug auf die herkömmliche Fourier-Transformation weist sie mehrere Ähnlichkeiten und Unterschiede auf. Die Fourier-Transformation wandelt eine Sequenz in eine durchgezogene Linie um. Auf diese Weise wird gesagt, dass das Ergebnis der Fourier-Variablen eine komplexe Funktion einer realen Variablen ist.
Die diskrete Fourier-Transformation empfängt im Gegensatz dazu ein diskretes Signal und transformiert es in ein anderes diskretes Signal, dh eine Sequenz.
Wofür ist die diskrete Fourier-Transformation??
Sie dienen in erster Linie dazu, Gleichungen erheblich zu vereinfachen und abgeleitete Ausdrücke in Potenzelemente umzuwandeln. Bezeichnen von Differentialausdrücken in Form integrierbarer Polynome.
Bei der Optimierung, Modulation und Modellierung von Ergebnissen fungiert es als standardisierter Ausdruck und ist nach mehreren Generationen eine häufige Ressource für das Engineering.
Geschichte
Dieses mathematische Konzept wurde 1811 von Joseph B. Fourier vorgestellt, während er eine Abhandlung über die Wärmeverteilung. Es wurde schnell von verschiedenen Zweigen der Wissenschaft und Technik übernommen.
Es wurde als Hauptarbeitsinstrument bei der Untersuchung von Gleichungen mit partiellen Ableitungen etabliert und sogar mit der bestehenden Arbeitsbeziehung zwischen den verglichen Laplace-Transformation und gewöhnliche Differentialgleichungen.
Jede Funktion, die mit einer Fourier-Transformation bearbeitet werden kann, muss außerhalb eines definierten Parameters null darstellen.
Diskrete Fourier-Transformation und ihre Umkehrung
Die diskrete Transformation wird durch den Ausdruck erhalten:
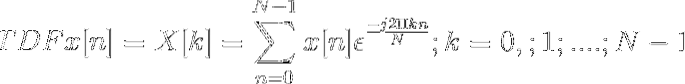
Nach gegebener diskreter Sequenz X [n]
Die Umkehrung der diskreten Fourier-Transformation wird durch den Ausdruck definiert:
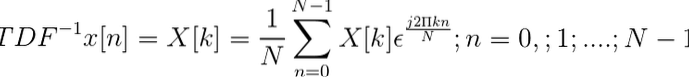
Sobald die diskrete Transformation erreicht wurde, kann die Sequenz im Zeitbereich X [n] definiert werden..
Geflügelt
Der der diskreten Fourier-Transformation entsprechende Parametrisierungsprozess liegt in der Fensterung. Um die Transformation durchzuführen, müssen wir die Reihenfolge zeitlich begrenzen. In vielen Fällen weisen die fraglichen Signale diese Einschränkungen nicht auf.
Eine Sequenz, die die Größenkriterien für die diskrete Transformation nicht erfüllt, kann mit einer "Fenster" -Funktion V [n] multipliziert werden, die das Verhalten der Sequenz in einem gesteuerten Parameter definiert.
X [n]. V [n]
Die Breite des Spektrums hängt von der Breite des Fensters ab. Mit zunehmender Breite des Fensters wird die berechnete Transformation enger.
Anwendungen
Berechnung der Grundlösung
Die diskrete Fourier-Transformation ist ein leistungsfähiges Werkzeug zur Untersuchung diskreter Sequenzen.
Die diskrete Fourier-Transformation transformiert eine kontinuierliche variable Funktion in eine diskrete variable Transformation.
Das Cauchy-Problem für die Wärmegleichung stellt ein häufiges Anwendungsfeld der diskreten Fourier-Transformation dar. Wo die Funktion generiert wird Wärmekern oder Dirichlet-Kern, Dies gilt für die Abtastung von Werten in einem definierten Parameter.
Signaltheorie
Der allgemeine Grund für die Anwendung der diskreten Fourier-Transformation in diesem Zweig liegt hauptsächlich in der charakteristischen Zerlegung eines Signals als unendliche Überlagerung leichter behandelbarer Signale.
Es kann eine Schallwelle oder eine elektromagnetische Welle sein, die diskrete Fourier-Transformation drückt sie in einer Überlagerung einfacher Wellen aus. Diese Darstellung ist in der Elektrotechnik recht häufig.
Die Fourier-Reihe
Sie sind Reihen, die in Bezug auf Cosinus und Sinus definiert sind. Sie dienen dazu, die Arbeit mit allgemeinen periodischen Funktionen zu erleichtern. Wenn sie angewendet werden, sind sie Teil der Techniken zum Lösen gewöhnlicher und partieller Differentialgleichungen..
Die Fourier-Reihen sind noch allgemeiner als die Taylor-Reihen, da sie periodische diskontinuierliche Funktionen entwickeln, die keine Taylor-Reihen-Darstellung haben..
Andere Formen der Fourier-Reihe
Um die Fourier-Transformation analytisch zu verstehen, ist es wichtig, die anderen Möglichkeiten zu überprüfen, wie die Fourier-Reihe gefunden werden kann, bis wir die Fourier-Reihe in ihrer komplexen Notation definieren können..
-Fourier-Reihen auf einer 2L-Periodenfunktion:
Oft ist es notwendig, die Struktur einer Fourier-Reihe an periodische Funktionen anzupassen, deren Periode im Intervall [-L, L] p = 2L> 0 ist..
-Fourier-Reihen in ungeraden und geraden Funktionen
Das Intervall [-π, π] wird berücksichtigt, was Vorteile bietet, wenn die symmetrischen Eigenschaften der Funktionen ausgenutzt werden.
Wenn f gerade ist, wird die Fourier-Reihe als eine Reihe von Cosinus erstellt.
Wenn f ungerade ist, wird die Fourier-Reihe als eine Reihe von Sinuswerten festgelegt.
-Komplexe Notation der Fourier-Reihe
Wenn wir eine Funktion f (t) haben, die alle Anforderungen der Fourier-Reihe erfüllt, ist es möglich, sie im Intervall [-t, t] mit ihrer komplexen Notation zu bezeichnen:
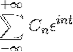
Beispiele
Zur Berechnung der Grundlösung werden folgende Beispiele vorgestellt:
Laplace-Gleichung
Wärmegleichung
Schrödinger-Gleichung
Wellengleichung
Andererseits sind die folgenden Beispiele für die Anwendung der diskreten Fourier-Transformation auf dem Gebiet der Signaltheorie:
-Systemidentifikationsprobleme. Etabliert f und g
-Problem mit der Konsistenz des Ausgangssignals
-Probleme mit der Signalfilterung
Ausbildung
Übung 1
Berechnen Sie die diskrete Fourier-Transformation für die folgende Sequenz.
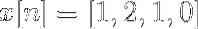
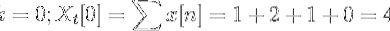
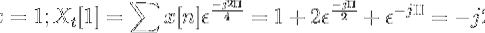
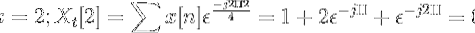
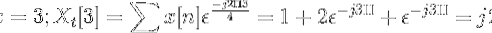
Sie können die Zapfwelle von x [n] wie folgt definieren:
X.t[k] = 4, -j2, 0, j2 für k = 0, 1, 2, 3
Übung 2
Wir wollen durch einen digitalen Algorithmus das durch den Ausdruck x (t) = e definierte Spektralsignal bestimmen-t. Wenn der maximale Frequenzanforderungskoeffizient f istm= 1 Hz. Eine Harmonische entspricht f = 0,3 Hz. Der Fehler ist auf weniger als 5% begrenzt. Berechnung F.s , D und N..
Unter Berücksichtigung des Stichprobensatzes F.s = 2fm = 2 Hz
Eine Frequenzauflösung von F.0 = 0,1 Hz, von wo Sie erhalten D = 1 / 0.1 = 10s
0,3 Hz ist die Frequenz, die dem Index k = 3 entspricht, wobei N = 3 × 8 = 24 Abtastwerte. Anzeigt, dass F.s = N / A = 24/10 = 2,4> 2
Da das Ziel darin besteht, den niedrigstmöglichen Wert für N zu erhalten, können die folgenden Werte als Lösung betrachtet werden:
F.0 = 0,3 Hz
D = 1 / 0,3 = 3,33 s
k = 1
N = 1 × 8 = 8
Verweise
- Beherrschung der diskreten Fourier-Transformation in einer, zwei oder mehreren Dimensionen: Fallstricke und Artefakte. Isaac Amidror. Springer Science & Business Media, 19. Juli. 2013
- Die DFT: Eine Bedienungsanleitung für die diskrete Fourier-Transformation. William L. Briggs, Van Emden Henson. SIAM, 1. Januar. 1995
- Digitale Signalverarbeitung: Theorie und Praxis. D. Sundararajan. World Scientific, 2003
- Transformationen und schnelle Algorithmen für die Signalanalyse und -darstellung. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6. Dezember. 2012
- Diskrete und kontinuierliche Fourier-Transformationen: Analyse, Anwendungen und schnelle Algorithmen. Eleanor Chu. CRC Press, 19. März. 2008



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.