Das Pascals Fass Es war ein Experiment, das der französische Wissenschaftler Blaise Pascal 1646 durchgeführt hatte, um definitiv zu demonstrieren, dass sich der Druck einer Flüssigkeit unabhängig von der Form des Behälters auf dieselbe Weise ausbreitet..
Das Experiment besteht darin, ein Fass mit einem dünnen und sehr hohen Rohr zu füllen, das perfekt auf den Einfüllstutzen abgestimmt ist. Wenn die Flüssigkeit eine Höhe von ungefähr 10 Metern erreicht (Höhe entspricht 7 gestapelten Fässern), platzt der Zylinder aufgrund des Drucks, den die Flüssigkeit in dem engen Rohr ausübt.
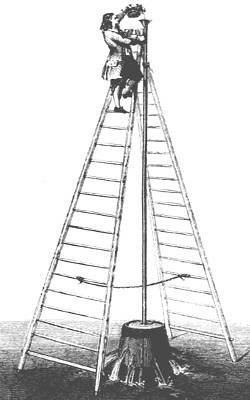
Der Schlüssel zum Phänomen liegt darin, das Konzept des Drucks zu verstehen. Der Druck P. Von einer Flüssigkeit auf eine Oberfläche ausgeübt wird die Gesamtkraft F. auf dieser Fläche geteilt durch die Fläche ZU der genannten Oberfläche:
P = F / A.
Artikelverzeichnis
Um die physikalischen Prinzipien von Pascals Experiment zu verstehen, berechnen wir den Druck am Boden eines Weinfasses, das sich mit Wasser füllt. Zur Vereinfachung der Berechnungen nehmen wir an, dass es zylindrisch mit den folgenden Abmessungen ist: Durchmesser 90 cm und Höhe 130 cm.
Wie gesagt, der Druck P. Tief im Inneren ist die Gesamtkraft F. im Hintergrund geteilt durch die Fläche ZU Vom Boden:
P = F / A.
Das Gebiet ZU von unten ist pi mal (π≈3.14) das Radio R. vom unteren Quadrat:
A = π⋅R ^ 2
Im Falle des Fasses beträgt er 6362 cm², was 0,6362 m² entspricht.
Die Kraft F. Am Boden des Fasses befindet sich das Gewicht des Wassers. Dieses Gewicht kann durch Multiplikation der Dichte berechnet werden ρ von Wasser durch das Wasservolumen und durch die Beschleunigung der Schwerkraft G.
F = ρ⋅A⋅h⋅g
Im Fall des mit Wasser gefüllten Fasses haben wir:
F = ρ⋅A⋅h⋅g = 1000 (kg / m ^ 3) ⋅0,6362 m 21,30 m 10 (m / s 2) = 8271 N..
Die Kraft wurde in Newton berechnet und entspricht 827 kg-f, ein Wert, der ziemlich nahe an einer Tonne liegt. Der Druck am Boden des Laufs beträgt:
P = F / A = 8271 N / 0,6362 m 2 = 13000 Pa = 13 kPa.
Der Druck wurde in Pascal (Pa) berechnet, der Druckeinheit im internationalen SI-Messsystem. Eine Druckatmosphäre entspricht 101325 Pa = 101,32 kPa.
Betrachten wir ein kleines Rohr mit einem Innendurchmesser von 1 cm und einer Höhe, die der eines Fasses entspricht, dh 1,30 Meter. Das Rohr wird vertikal platziert, wobei sein unteres Ende mit einer kreisförmigen Kappe verschlossen ist und an seinem oberen Ende mit Wasser gefüllt ist.
Berechnen wir zunächst die Fläche des Rohrbodens:
A = π⋅R ^ 2 = 3,14 * (0,5 cm) ^ 2 = 0,785 cm ^ 2 = 0,0000785 m ^ 2.
Das Gewicht des im Rohr enthaltenen Wassers wird nach folgender Formel berechnet:
F = ρ⋅A⋅h⋅g = 1000 (kg / m ^ 3) ⋅0.0000785 m ^ 21,30 m 10 (m / s 2) = 1,0 N..
Das heißt, das Gewicht des Wassers beträgt 0,1 kg-f, dh nur 100 g.
Berechnen wir nun den Druck:
P = F / A = 1 N / 0,0000785 m 2 = 13000 Pa = 13 kPa.
Tolle! Der Druck ist der gleiche wie der eines Fasses. Dies ist das hydrostatische Paradoxon.
Der Druck am Boden von Pascals Fass ist die Summe des Drucks, der durch das im Fass selbst enthaltene Wasser erzeugt wird, plus dem Druck des Wassers in einem schmalen Rohr mit einer Höhe von 9 Metern und einem Durchmesser von 1 cm, das mit dem Mund verbunden ist. Fassfüllung.
P = F / A = ρ⋅A⋅h⋅g / A = ρ⋅g⋅h = 1000 · 10 · 9 Pa = 90000 Pa = 90 kPa.
Beachten Sie, dass im vorherigen Ausdruck der Bereich ZU Es wurde abgebrochen, egal ob es sich um eine große oder kleine Fläche wie die Röhre handelt. Mit anderen Worten, der Druck hängt von der Höhe der Oberfläche in Bezug auf den Boden ab, unabhängig vom Durchmesser..
Fügen wir diesem Druck den Druck des Laufs selbst am Boden hinzu:
P.Knirps = 90 kPa + 13 kPa = 103 kPa.
Um herauszufinden, wie viel Kraft auf den Boden des Zylinders ausgeübt wird, multiplizieren wir den Gesamtdruck mit der Fläche am Boden des Zylinders.
F.Knirps = P.Knirps * A = 103000 Pa * 0,6362 m 2 = 65529 N = 6553 kg-f.
Dies bedeutet, dass der Boden des Laufs 6,5 Tonnen Gewicht trägt.
Pascals Fassversuch ist zu Hause leicht reproduzierbar, sofern er in kleinerem Maßstab durchgeführt wird. Dazu müssen nicht nur die Abmessungen verkleinert, sondern auch der Lauf durch ein Glas oder einen Behälter mit geringerem Druckwiderstand ersetzt werden..
1- Einwegbecher aus Polystyrol mit Deckel. Nach Angaben des spanischsprachigen Landes wird Polystyrol auf verschiedene Arten genannt: Weißkork, Styropor, Polystyrol, Schaum, Anime und andere Namen. Diese Deckel finden Sie häufig in Fast-Food-Läden zum Mitnehmen..
2- Kunststoffschlauch, vorzugsweise transparent mit einem Durchmesser von 0,5 cm oder weniger und einer Länge zwischen 1,5 und 1,8 m.
3- Klebeband zum Verpacken.
- Durchstechen Sie den Deckel des Styroporbechers mit Hilfe eines Bohrers, eines Stempels, eines Rasierers oder eines Fräsers, so dass ein Loch entsteht, durch das der Schlauch fest verläuft.
- Führen Sie den Schlauch durch das Loch im Deckel, so dass ein kleiner Teil des Schlauchs in das Glas gelangt.
- Verschließen Sie die Schlauchverbindung mit der Kappe auf beiden Seiten der Kappe sorgfältig mit Klebeband.
- Setzen Sie den Deckel auf das Glas und verschließen Sie die Verbindung zwischen Deckel und Glas mit Klebeband, damit kein Wasser entweichen kann.
- Stellen Sie das Glas auf den Boden, und dann müssen Sie den Schlauch dehnen und anheben. Es kann hilfreich sein, mit einem Tropfen, einem Hocker oder einer Leiter aufzustehen.
- Füllen Sie das Glas mit Wasser durch den Schlauch. Ein kleiner Trichter an der Schlauchspitze erleichtert das Befüllen.
Wenn das Glas voll ist und der Wasserstand durch den Schlauch zu steigen beginnt, steigt der Druck. Es kommt eine Zeit, in der das Styroporglas dem Druck nicht standhält und platzt, wie Pascal mit seinem berühmten Fass demonstrierte.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.