Das Bernoullis Satz, Der Mathematiker und Physiker Daniel Bernoulli hat in seiner Arbeit das Verhalten einer in Bewegung befindlichen Flüssigkeit beschrieben Hydrodynamik. Nach dem Prinzip hat ein ideales Fluid (ohne Reibung oder Viskosität), das durch eine geschlossene Leitung zirkuliert, eine konstante Energie auf seinem Weg.
Der Satz kann aus dem Prinzip der Energieerhaltung und sogar aus Newtons zweitem Bewegungsgesetz abgeleitet werden. Darüber hinaus legt das Bernoulli-Prinzip auch fest, dass eine Zunahme der Geschwindigkeit eines Fluids eine Abnahme des Drucks, dem es ausgesetzt ist, eine Abnahme seiner potentiellen Energie oder beides gleichzeitig impliziert..
Der Satz hat viele verschiedene Anwendungen, sowohl in der Welt der Wissenschaft als auch im Alltag der Menschen..
Seine Folgen liegen unter anderem in der Auftriebskraft von Flugzeugen, in den Kaminen von Haushalten und Industrie, in Wasserleitungen..
Artikelverzeichnis
Obwohl Bernoulli derjenige war, der folgerte, dass der Druck mit zunehmender Strömungsgeschwindigkeit abnimmt, war es die Wahrheit, dass es Leonhard Euler war, der die Bernoulli-Gleichung tatsächlich in der Form entwickelte, in der sie heute bekannt ist..
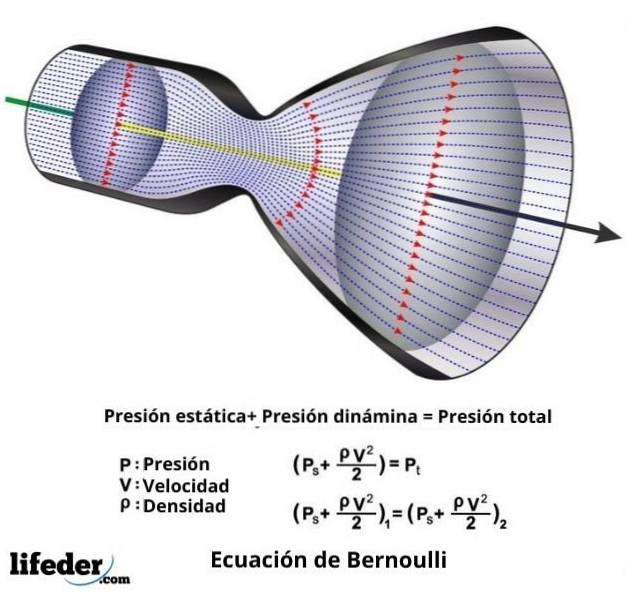
In jedem Fall lautet die Bernoulli-Gleichung, die nichts anderes als der mathematische Ausdruck seines Satzes ist, wie folgt:
vzwei ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = konstant
In diesem Ausdruck ist v die Geschwindigkeit des Fluids durch den betrachteten Abschnitt, ƿ ist die Dichte des Fluids, P ist der Druck des Fluids, g ist der Wert der Erdbeschleunigung und z ist die in der gemessene Höhe Richtung der Schwerkraft.
In Bernoullis Gleichung ist implizit enthalten, dass die Energie einer Flüssigkeit aus drei Komponenten besteht:
- Eine kinetische Komponente, die sich aus der Geschwindigkeit ergibt, mit der sich die Flüssigkeit bewegt.
- Eine potentielle oder Gravitationskomponente, die auf die Höhe zurückzuführen ist, in der sich die Flüssigkeit befindet.
- Eine Druckenergie, die diejenige ist, die das Fluid als Folge des Drucks besitzt, dem es ausgesetzt ist.
Andererseits kann die Bernoulli-Gleichung auch folgendermaßen ausgedrückt werden:
v1 zwei ∙ ƿ / 2 + P.1 + ƿ ∙ g ∙ z1 = vzweizwei ∙ ƿ / 2 + P.zwei + ƿ ∙ g ∙ zzwei
Dieser letzte Ausdruck ist sehr praktisch, um die Änderungen zu analysieren, die eine Flüssigkeit erfährt, wenn sich eines der Elemente, aus denen die Gleichung besteht, ändert.
In bestimmten Fällen ist die Änderung des ρgz-Terms der Bernoulli-Gleichung im Vergleich zu den anderen Begriffen minimal, so dass sie vernachlässigt werden kann. Dies geschieht beispielsweise bei Strömungen, die ein Flugzeug im Flug erfährt..
Bei diesen Gelegenheiten wird die Bernoulli-Gleichung wie folgt ausgedrückt:
P + q = P.0
In diesem Ausdruck ist q dynamischer Druck und entspricht v zwei ∙ ƿ / 2 und P.0 ist der sogenannte Gesamtdruck und ist die Summe des statischen Drucks P und des dynamischen Drucks q.
Der Satz von Bernoulli hat viele und unterschiedliche Anwendungen in so unterschiedlichen Bereichen wie Wissenschaft, Technik, Sport usw..
Eine interessante Anwendung findet sich in der Gestaltung von Kaminen. Die Schornsteine sind hoch gebaut, um einen größeren Druckunterschied zwischen Boden und Schornsteinauslass zu erzielen, wodurch die Verbrennungsgase leichter abgesaugt werden können.
Natürlich gilt die Bernoulli-Gleichung auch für die Untersuchung der Bewegung von Flüssigkeitsströmen in Rohren. Aus der Gleichung folgt, dass eine Verringerung der Querschnittsfläche des Rohrs, um die Geschwindigkeit des durchströmenden Fluids zu erhöhen, auch einen Druckabfall impliziert.
Die Bernoulli-Gleichung wird auch in der Luftfahrt und in Formel-1-Fahrzeugen verwendet. In der Luftfahrt ist der Bernoulli-Effekt der Ursprung des Auftriebs von Flugzeugen.
Flugzeugflügel sind mit dem Ziel konstruiert, einen größeren Luftstrom an der Oberseite des Flügels zu erreichen.
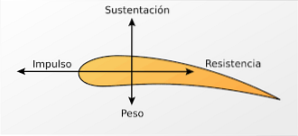
Somit ist im oberen Teil des Flügels die Luftgeschwindigkeit hoch und daher der Druck niedriger. Diese Druckdifferenz erzeugt eine vertikal nach oben gerichtete Kraft (Auftriebskraft), die es dem Flugzeug ermöglicht, in der Luft zu schweben. Ein ähnlicher Effekt wird bei den Querrudern von Formel-1-Fahrzeugen erzielt.
Durch ein Rohr mit einem Querschnitt von 4,2 cmzwei ein Wasserstrahl fließt mit 5,18 m / s. Das Wasser steigt von einer Höhe von 9,66 m auf eine niedrigere Ebene mit einer Höhe von null an, während die Querschnittsfläche des Rohrs auf 7,6 cm ansteigtzwei.
a) Berechnen Sie die Geschwindigkeit des Wasserstroms auf der unteren Ebene.
b) Bestimmen Sie den Druck auf der unteren Ebene, wobei Sie wissen, dass der Druck auf der oberen Ebene 152000 Pa beträgt.
a) Da der Fluss erhalten bleiben muss, gilt Folgendes:
Q.Höheres Niveau = Q.niedrigeres Level
v1 . S.1 = vzwei . S.zwei
5,18 m / s. 4,2 cmzwei = vzwei . 7,6 cm ^zwei
Wenn man nach löst, erhält man, dass:
vzwei = 2,86 m / s
b) Anwendung des Bernoulli-Theorems zwischen den beiden Ebenen und Berücksichtigung der Wasserdichte von 1000 kg / m3 , es wird erhalten, dass:
v1 zwei ∙ ƿ / 2 + P.1 + ƿ ∙ g ∙ z1 = vzweizwei ∙ ƿ / 2 + P.zwei + ƿ ∙ g ∙ zzwei
(1/2). 1000 kg / m3 . (5,18 m / s)zwei + 152000 + 1000 kg / m3 . 10 m / szwei . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)zwei + P.zwei + 1000 kg / m3 . 10 m / szwei . 0 m
Auflösen nach P.zwei Sie kommen zu:
P.zwei = 257926,4 Pa
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.