Das axiale Symmetrie Es tritt auf, wenn die Punkte einer Figur mit den Punkten einer anderen Figur mittels einer geraden Winkelhalbierenden, die als Symmetrieachse bezeichnet wird, zusammenfallen. Es wird auch als radiale, rotatorische oder zylindrische Symmetrie bezeichnet..
Es wird normalerweise in geometrischen Figuren angewendet, ist aber in der Natur leicht zu beobachten, da es Tiere wie Schmetterlinge, Skorpione, Marienkäfer oder Menschen gibt, die axiale Symmetrie aufweisen..
Artikelverzeichnis
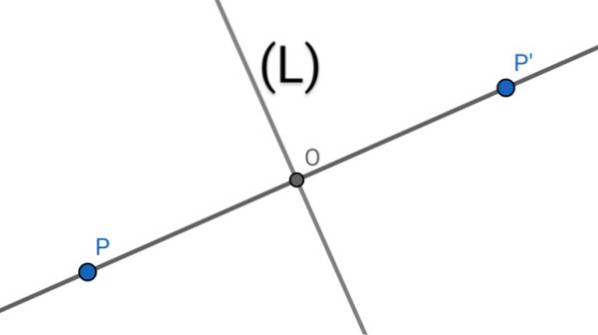
Um die axiale Symmetrie P 'eines Punktes P in Bezug auf eine Linie (L) zu ermitteln, werden die folgenden geometrischen Operationen ausgeführt:
1.- Die Senkrechte zu der Linie (L), die durch Punkt P verläuft, wird gezeichnet.
2.- Das Abfangen der beiden Linien bestimmt einen Punkt O..
3.- Die Länge des Segments PO wird gemessen, dann wird diese Länge über die Linie (PO) kopiert, beginnend von O in der Richtung von P nach O, wobei der Punkt P 'bestimmt wird.
4.- Punkt P 'ist die axiale Symmetrie von Punkt P in Bezug auf die Achse (L), da die Linie (L) die Mittlermatrix des Segments PP' ist, wobei O der Mittelpunkt des Segments ist.
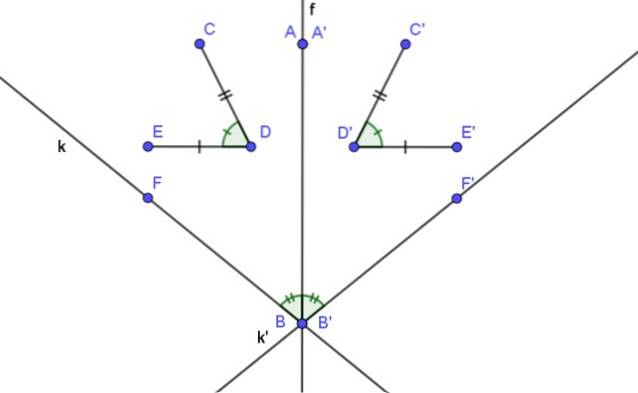
- Die axiale Symmetrie ist isometrisch, dh die Abstände einer geometrischen Figur und ihre entsprechende Symmetrie bleiben erhalten.
- Das Maß eines Winkels und das seiner Symmetrie sind gleich.
- Die axiale Symmetrie eines Punktes auf der Symmetrieachse ist der Punkt selbst.
- Die symmetrische Linie einer Linie parallel zur Symmetrieachse ist auch eine Linie parallel zu dieser Achse.
- Eine Sekantenlinie zur Symmetrieachse hat als symmetrische Linie eine andere Sekantenlinie, die wiederum die Symmetrieachse am gleichen Punkt der ursprünglichen Linie schneidet.
- Das symmetrische Bild einer Linie ist eine weitere Linie, die mit der Symmetrieachse einen Winkel bildet, der dem Maß der ursprünglichen Linie entspricht.
- Das symmetrische Bild einer Linie senkrecht zur Symmetrieachse ist eine weitere Linie, die die erste überlappt.
- Eine Linie und ihre axialsymmetrische Linie bilden einen Winkel, dessen Winkelhalbierende die Symmetrieachse ist.
Die Natur weist zahlreiche Beispiele für axiale Symmetrie auf. Zum Beispiel können Sie unter anderem die Symmetrie von Gesichtern, Insekten wie Schmetterlingen, die Reflexion auf ruhigen Wasseroberflächen und Spiegeln oder die Blätter von Pflanzen sehen..
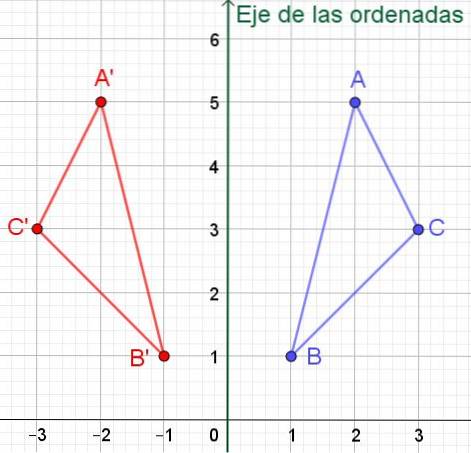
Wir haben das Dreieck der Eckpunkte A, B und C, deren kartesische Koordinaten jeweils A = (2, 5), B = (1, 1) und C = (3,3) sind. Finden Sie die kartesischen Koordinaten des Dreiecks symmetrisch zur Y-Achse (Ordinatenachse).
Lösung: Wenn ein Punkt P Koordinaten (x, y) hat, ist seine Symmetrie um die Ordinatenachse (Y-Achse) P '= (- x, y). Das heißt, der Wert seiner Abszisse ändert das Vorzeichen, während der Wert der Ordinate gleich bleibt.
In diesem Fall hat das symmetrische Dreieck mit den Eckpunkten A ', B' und C 'folgende Koordinaten:
A '= (- 2, 5); B '= (- 1, 1) und C' = (- 3, 3), wie in 6 zu sehen ist.
Überprüfen Sie anhand des Dreiecks ABC und seines symmetrischen A'B'C 'aus Übung 1, ob die entsprechenden Seiten des ursprünglichen Dreiecks und seines symmetrischen Dreiecks dieselbe Länge haben.
Lösung: Um den Abstand oder die Länge der Seiten zu ermitteln, verwenden wir die euklidische Abstandsformel:
d (A, B) = √ ((Bx - Ax) ^ 2 + (By - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1) ) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
Die Länge der entsprechenden symmetrischen Seite A'B 'wird nachstehend berechnet:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
Auf diese Weise wird überprüft, ob die axiale Symmetrie den Abstand zwischen zwei Punkten beibehält. Der Vorgang kann für die beiden anderen Seiten des Dreiecks und dessen Symmetrie wiederholt werden, um die Invarianz in der Länge zu überprüfen. Zum Beispiel | AC | = | A'C '| = √5 = 2,236.
Überprüfen Sie in Bezug auf das Dreieck ABC und sein symmetrisches A'B'C 'aus Übung 1, ob die entsprechenden Winkel des ursprünglichen Dreiecks und seines symmetrischen Dreiecks das gleiche Winkelmaß haben.
Lösung: Um die Maße der Winkel BAC und B'A'C 'zu bestimmen, wird zuerst das Skalarprodukt der Vektoren berechnet AB mit AC und dann das Punktprodukt von A'B ' mit A'C '.
Daran erinnern:
A = (2, 5), B = (1, 1) und C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) und C' = (- 3, 3).
Es hat:
AB = <1-2, 1-5> Y. AC = <3-2, 3-5>
ähnlich
A'B ' = <-1+2, 1-5> Y. AC = <-3+2, 3-5>
Dann werden die folgenden skalaren Produkte gefunden:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
Ähnlich
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
Das Maß für den Winkel BAC ist:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅ |AC |)) =
ArcCos (7 / (4,123⋅2,236)) = 40,6º
In ähnlicher Weise ist das Maß des Winkels B'A'C ':
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (|A'B '|⋅ |A'C '|)) =
ArcCos (7 / (4,123⋅2,236)) = 40,6º
Daraus folgt, dass die axiale Symmetrie das Winkelmaß beibehält.
Sei ein Punkt P der Koordinaten (a, b). Finden Sie die Koordinaten seiner axialen Symmetrie P 'in Bezug auf die Linie y = x.
Lösung: Wir werden (a ', b') die Koordinaten des symmetrischen Punktes P 'in Bezug auf die Linie y = x nennen. Der Mittelpunkt M des Segments PP 'hat Koordinaten ((a + a') / 2, (b + b ') / 2) und liegt ebenfalls auf der Linie y = x, so dass die folgende Gleichheit wahr ist:
a + a '= b + b'
Andererseits hat das Segment PP 'eine Steigung -1, weil es senkrecht zur Linie y = x mit Steigung 1 ist, so dass die folgende Gleichheit gilt:
b - b '= a' -a
Wenn nach den beiden vorherigen Gleichungen a 'und b' gelöst wird, wird der Schluss gezogen, dass:
a '= b und das b' = a.
Das heißt, wenn ein Punkt P (a, b) gegeben ist, ist seine axiale Symmetrie in Bezug auf die Linie y = x P '(b, a).
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.