Das schräge Linien Dies sind diejenigen, die entweder in Bezug auf eine flache Oberfläche oder in Bezug auf eine andere Gerade, die eine bestimmte Richtung angibt, geneigt sind. Betrachten Sie als Beispiel die drei Linien, die in einer Ebene gezeichnet sind und in der folgenden Abbildung dargestellt sind.
Wir kennen ihre jeweiligen relativen Positionen, weil wir sie mit einer Referenzlinie vergleichen, die normalerweise die ist X-Achse bezeichnet die Horizontale.
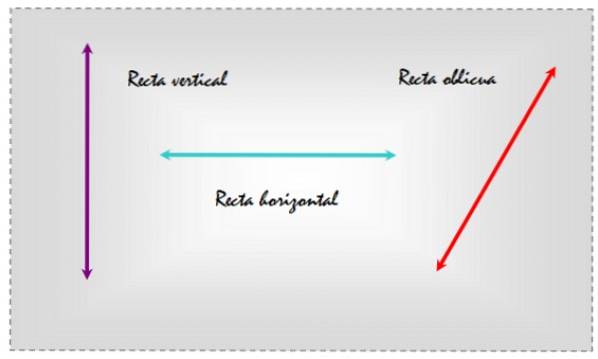
Auf diese Weise ist bei Auswahl der Horizontalen als Referenz die Linie links vertikal, die Linie in der Mitte horizontal und die Linie rechts schräg, da sie in Bezug auf die alltäglichen Referenzlinien geneigt ist..
Jetzt nehmen die Linien, die sich auf derselben Ebene befinden, wie z. B. die Oberfläche des Papiers oder des Bildschirms, unterschiedliche Positionen ein relative Positionen einander, je nachdem, ob sie sich schneiden oder nicht. Im ersten Fall handelt es sich um Sekantenlinien, im zweiten Fall sind sie parallel.
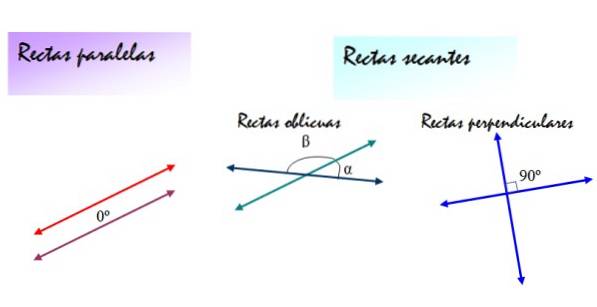
Andererseits können die Sekantenlinien schräge Linien oder senkrechte Linien sein. In beiden Fällen sind die Steigungen der Linien unterschiedlich, aber die schrägen Linien bilden zwischen ihnen Winkel α und β, die sich von 90 ° unterscheiden, während die durch die senkrechten Linien bestimmten Winkel immer 90 ° betragen..
Die folgende Abbildung fasst diese Definitionen zusammen:
Artikelverzeichnis
Um die relativen Positionen der Linien in der Ebene zu kennen, muss der Winkel bekannt sein, den sie miteinander bilden. Beachten Sie, dass die Zeilen sind:
Parallel: Wenn sie die gleiche Neigung (gleiche Richtung) haben und sich nie schneiden, sind ihre Punkte äquidistant.
Zufall: Wenn alle Punkte zusammenfallen und daher die gleiche Steigung haben, der Abstand zwischen den Punkten jedoch Null ist.
Trocknen: Wenn ihre Steigungen unterschiedlich sind, variiert der Abstand zwischen ihren Punkten und der Schnittpunkt ist ein einzelner Punkt.
Eine Möglichkeit, festzustellen, ob zwei Linien in der Ebene sekant oder parallel sind, besteht in ihrer Neigung. Die Kriterien für Parallelität und Rechtwinkligkeit der Linien sind folgende:
Sei L zwei Zeilen1 und ichzwei Zugehörigkeit zu einer Ebene, deren Steigungen jeweils m sind1 und Mzwei. Diese Linien sind parallel, wenn m1 = mzwei und sind senkrecht, wenn m1= -1 / mzwei
Wenn bei Kenntnis der Steigungen zweier Linien in der Ebene keines der vorherigen Kriterien erfüllt ist, schließen wir, dass die Linien schräg sind. Wenn Sie zwei Punkte einer Linie kennen, wird die Steigung sofort berechnet, wie wir im nächsten Abschnitt sehen werden.
Es ist möglich herauszufinden, ob zwei Linien sekant oder parallel sind, indem man ihren Schnittpunkt findet und das Gleichungssystem löst, das sie bilden: Wenn es eine Lösung gibt, sind sie Sekanten, wenn es keine Lösung gibt, sind sie parallel, aber wenn die Lösungen sind unendlich, die Linien fallen zusammen.
Dieses Kriterium informiert uns jedoch nicht über den Winkel zwischen diesen Linien, selbst wenn sie sich schneiden.
Um den Winkel zwischen den Linien zu kennen, werden zwei Vektoren benötigt oder Y. v das gehört jedem von ihnen. Somit ist es möglich, den Winkel, den sie bilden, anhand des Skalarprodukts der Vektoren zu kennen, das auf diese Weise definiert wird:
oder• •v =u.v.cos α
Eine Linie in der kartesischen Ebene kann auf verschiedene Arten dargestellt werden, z.
-Steigungsschnittform: Ja m ist die Steigung der Linie und b ist der Schnittpunkt der Linie mit der vertikalen Achse, die Gleichung der Linie ist y = mx + b.
-Allgemeine Gleichung für eine gerade Linie:: Axe + By + C = 0, wo m = A / B. ist die Steigung.
In der kartesischen Ebene sind die vertikalen und horizontalen Linien besondere Fälle der Liniengleichung.
-Vertikale Linien:: x = a
-Horizontale Linien:: y = k
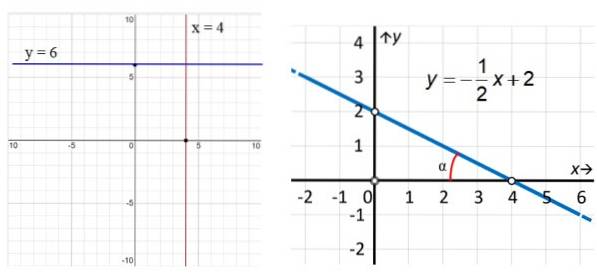
In den Beispielen in Abbildung 3 hat die vertikale rote Linie die Gleichung x = 4, während die Linie parallel zur x-Achse (blau) die Gleichung y = 6 hat. Was die Linie rechts betrifft, sehen wir, dass sie schräg und zu ist Um seine Gleichung zu finden, verwenden wir die in der Abbildung hervorgehobenen Punkte: (0,2) und (4,0) auf folgende Weise:
m = (undzwei - Y.1) / (xzwei - x1) = (2 - 0) / (0 - 4) = - ½
Der Schnitt dieser Linie mit der vertikalen Achse ist y = 2, wie aus der Grafik ersichtlich ist. Mit diesen Informationen:
y = (-½) x + 2
Die Bestimmung des Neigungswinkels zur x-Achse ist einfach. Ich fühle, dass:
α = arctg (2/4) = 26,6º
Daher beträgt der positive Winkel von der x-Achse zur Linie: 180º - 26,6º = 153,4º
An vielen Stellen treten schräge Linien auf. Es ist wichtig, darauf zu achten, dass sie in Architektur, Sport, Stromversorgungskabeln, Rohren und vielen anderen Orten zu finden sind. In der Natur sind auch schräge Linien vorhanden, wie wir unten sehen werden:
Das Sonnenlicht bewegt sich in einer geraden Linie, aber die abgerundete Form der Erde beeinflusst, wie das Sonnenlicht auf die Oberfläche trifft..
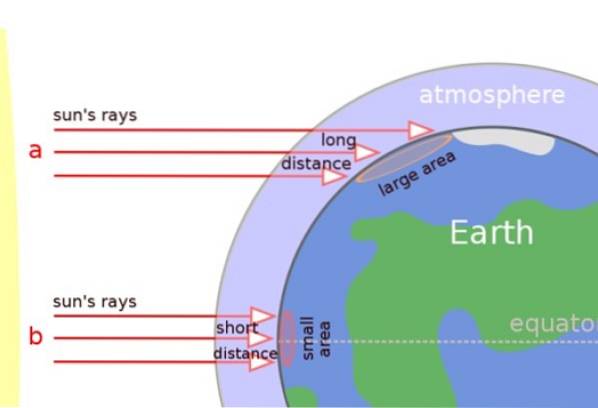
Im Bild unten sehen wir deutlich, dass die Sonnenstrahlen in tropischen Regionen senkrecht auftreffen, in gemäßigten Regionen und an den Polen jedoch schräg die Oberfläche erreichen..
Aus diesem Grund bewegen sich die Sonnenstrahlen über eine längere Strecke durch die Atmosphäre und die Wärme wird auf einer größeren Oberfläche verteilt (siehe Abbildung). Das Ergebnis ist, dass die Bereiche in der Nähe der Pole kälter sind.
Wenn sich zwei Linien nicht in derselben Ebene befinden, können sie immer noch schräg sein oder verzogen, wie sie auch bekannt sind. In diesem Fall sind ihre Direktorvektoren nicht parallel, aber da sie nicht zur gleichen Ebene gehören, schneiden sich diese Linien nicht.
Zum Beispiel befinden sich die Linien in Abbildung 6 rechts eindeutig auf verschiedenen Ebenen. Wenn Sie sie von oben betrachten, können Sie sehen, dass sie sich zwar schneiden, aber keinen gemeinsamen Punkt haben. Rechts sehen wir die Räder des Fahrrads, deren Speichen sich von vorne gesehen zu kreuzen scheinen.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.