
Hydrostatische Druckformel, Berechnung, Beispiele, Übungen

Das hydrostatischer Druck ist diejenige, die eine Flüssigkeit an jedem Punkt in ihrem Inneren im statischen Gleichgewicht ausübt, sei es eine darin eingetauchte Oberfläche, die Wände des Behälters oder ein Teil der Flüssigkeit, der Teil der Gesamtmasse ist.
Die Art und Weise, wie Flüssigkeiten Druck ausüben, unterscheidet sich von Feststoffen. Diese üben Druck nach unten aus, aber eine Flüssigkeit oder ein Gas tut dies in alle Richtungen.

Wenn es um eine Flüssigkeit geht, steigt der Druck mit der Tiefe, wie aus Erfahrung beim Eintauchen in Wasser bekannt ist, in dem der Druckanstieg in den Ohren spürbar ist. Dieser Druck ergibt sich aus dem Gewicht der Flüssigkeit und der unaufhörlichen Bewegung der Partikel, aus denen sie besteht, die kontinuierlich auf die in die Flüssigkeit eingetauchte Oberfläche des Körpers treffen..
Wenn wir von einer inkompressiblen Flüssigkeit ausgehen - was bei den meisten Anwendungen der Fall ist -, bleibt ihre Dichte konstant, und in diesem Fall hängt der Druck linear von der Tiefe ab..
Artikelverzeichnis
- 1 Formel
- 2 Beispiele für hydrostatischen Druck
- 2.1 Strukturen, bei denen hydrostatischer Druck relevant ist
- 3 Übungen
- 3.1 - Übung 1
- 3.2 - Übung 2
- 4 Referenzen
Formel
Der hydrostatische Druck wird unter Verwendung des folgenden Ausdrucks berechnet:
P = P.Geldautomat + ρ · g · h
Wo:
-P der an einem Punkt ausgeübte Druck
-P.Geldautomat ist der Druck der Atmosphäre an der freien Oberfläche
-ρ ist die Dichte der Flüssigkeit
-g ist die Erdbeschleunigung
-h ist die Tiefe, in der Sie den hydrostatischen Druck berechnen möchten
Die Formel enthält die Auswirkungen der Atmosphäre, aber viele Manometer oder Manometer setzen 0 in den atmosphärischen Druck. Aus diesem Grund messen sie den Differenzdruck oder den relativen Druck, der auch als Druck bezeichnet wird Manometerdruck::
P.m = ρ · g · h
Gase komprimieren oder dehnen sich sehr leicht aus. Daher ist seine Dichte, dh das Verhältnis zwischen Masse und Volumen, normalerweise eine Funktion anderer Parameter wie Höhe und Temperatur bei atmosphärischen Gasen..
Der von Gasen ausgeübte Druck wird oft genannt aerostatischer Druck, Der Begriff hydrostatischer Druck ist Flüssigkeiten vorbehalten.
Beispiele für hydrostatischen Druck
Der hydrostatische Druck hängt nur von der Tiefe ab, daher ist die Form oder Fläche des Bodens des Behälters nicht relevant.
Da der Druck P als senkrechte Kraftkomponente F pro Flächeneinheit A definiert ist:
P = F / A.
Dann kann die von der Flüssigkeit am Boden eines Behälters ausgeübte Kraft unterschiedlich sein, aber da sie über verschiedene Ausdehnungen verteilt ist, ist der Druck, der das Kraft / Flächen-Verhältnis ist, für Punkte in derselben Tiefe gleich..
Betrachten Sie die Behälter in der Abbildung. Der Druck ist für alle roten Punkte, die sich auf dem gleichen Niveau befinden, gleich, obwohl sich im zentralen Behälter eine größere Flüssigkeitsmenge über diesem Niveau befindet - breiter - als das zylindrische und dünne Rohr ganz links..
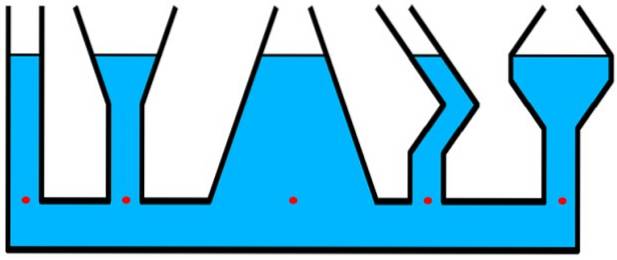
Strukturen, bei denen hydrostatischer Druck relevant ist
-Die Wände eines Damms: Obwohl die Kraft für alle Punkte des flachen Bodens gleich ist, wächst sie an der vertikalen Wand mit zunehmender Tiefe. Deshalb sind die Stützmauern an der Basis breiter als oben.
-An den Wänden und am Boden eines Schwimmbades.
-In Sternen wie unserer Sonne, wo der hydrostatische Druck die Schwerkraft ausgleicht und den Stern am Laufen hält. Wenn dieses Gleichgewicht gebrochen ist, kollabiert der Stern und unterliegt extremen Änderungen in seiner Struktur..
-Flüssigkeitsspeichertanks, die dem hydrostatischen Druck standhalten. Nicht nur die Wände, sondern auch die Tore, die das Befüllen und Herausziehen erleichtern. Bei seiner Auslegung wird berücksichtigt, ob die Flüssigkeit ätzend ist und auch der Druck und die Kraft, die sie ausübt, entsprechend ihrer Dichte.
-Reifen und Ballons, die so aufgepumpt sind, dass sie dem Druck der Flüssigkeit (Gas oder Flüssigkeit) widerstehen, ohne zu reißen.
-Jeder untergetauchte Körper, der dank des von der Flüssigkeit ausgeübten hydrostatischen Drucks einen vertikalen Aufwärtsschub oder eine "Aufhellung" seines Gewichts erfährt. Dies ist als die bekannt Archimedes Prinzip.
Ausbildung
Das Prinzip von Archimedes besagt, dass ein Körper, wenn er ganz oder teilweise eingetaucht ist, eine vertikale Kraft nach oben erfährt, die als Schub bezeichnet wird. Die Größe des Schubes ist numerisch gleich dem Gewicht des vom Objekt verdrängten Wasservolumens..

Sei ρFlüssigkeit die Dichte der Flüssigkeit, V.s das untergetauchte Volumen, g die Erdbeschleunigung und B die Größe des Schubes, die wir mit dem folgenden Ausdruck berechnen können:
B = ρFlüssigkeit .V.s .G
- Übung 1
Ein rechteckiger Block mit den Abmessungen 2,0 cm x 2,0 cm x 6,0 cm schwimmt mit seiner längsten vertikalen Achse im Süßwasser. Die Länge des Blocks, der über das Wasser hinausragt, beträgt 2,0 cm. Berechnen Sie die Dichte des Blocks.
Lösung
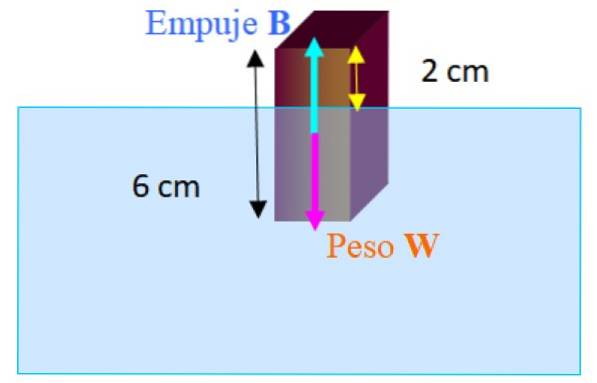
Die auf den Block einwirkenden Kräfte sind das Gewicht W. runter und stoßen B. nach oben. Wenn der Block im Gleichgewicht schwimmt, haben wir:
∑ F.Y. = B - W = 0
B = W.
Die Größe des Gewichts W ist das Produkt aus der Masse m des Blocks und der Erdbeschleunigung. Wir werden die Definition der Dichte ρ verwendenoder als Quotient zwischen der Masse m und die Lautstärke V. des Blocks:
ρoder = m / V → m = ρoder . V.
Der Schub ist seinerseits:
B = ρFlüssigkeit .V.s .G
Gleichsetzung von Schubgröße und Gewichtsgröße:
ρFlüssigkeit .V.s .g = ρoder . V.g.
Die Schwerkraft wird aufgehoben, indem sie auf beiden Seiten ein Faktor ist, und die Dichte des Blocks kann wie folgt gelöst werden:
ρoder = ρFlüssigkeit . (V.s / V)
Die Wasserdichte in Einheiten des Internationalen Systems beträgt 1000 kg / m3. Die Volumina betragen insgesamt V und untergetauchtes V.s, werden berechnet mit V = Breite x Höhe x Tiefe:
V = 2,0 cm × 2,0 cm × 6,0 cm = 24,0 cm3
V.s = 2,0 cm x 2,0 cm x 4,0 cm = 16,0 cm3
Werte ersetzen:
ρoder = ρFlüssigkeit . (V.s / V) = 1000 kg / m3 . (16/24) = 667 kg / m3
- Übung 2
Berechnen Sie den Prozentsatz des untergetauchten Volumens eines Eisstücks, das bei 0 ºC im Meerwasser schwimmt.
Lösung
Eis schwimmt auf Wasser, da seine Dichte geringer ist: 916,8 kg / m3, Dies bedeutet, dass es sich beim Abkühlen ausdehnt, im Gegensatz zu den meisten Substanzen, deren Volumen beim Erhitzen zunimmt.

Es ist ein sehr glücklicher Lebensumstand, da die Wassermassen nur an der Oberfläche gefrieren und in der Tiefe flüssig bleiben.
Die Dichte des Meerwassers ist etwas höher als die des Süßwassers: 1027 kg / m3. Wir werden den Volumenanteil V berechnens / V:
V.s / V = ρoder / ρFlüssigkeit = 916,8 kg / m3 / 1027 kg / m3 = 0,8927
Dies bedeutet, dass ungefähr 89% des Eises unter Wasser getaucht bleiben. Nur 11% sind auf dem Meer schwimmend sichtbar.
Verweise
- Giambattista, A. 2010. Physik. 2 .. Ed. McGraw Hill.
- Knight, R. 2017. Physik für Wissenschaftler und Ingenieure: ein strategischer Ansatz. Pearson.
- Cimbala, C. 2006. Strömungsmechanik, Grundlagen und Anwendungen. Mc. Graw Hill.
- Hibbeler, R. 2015. Strömungsmechanik. 1. Ed. Pearson.
- Mott, R. 2006. Fluid Mechanics. 4 .. Auflage. Pearson Ausbildung.
- Streeter, V. 1999. Fluid Mechanics. Mcgraw Hügel.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.