EIN perfekte Zahl ist eine natürliche Zahl, so dass Die Summe seiner Teiler entspricht der Zahl. Offensichtlich kann die Zahl selbst nicht zwischen den Teilern eingeschlossen werden.
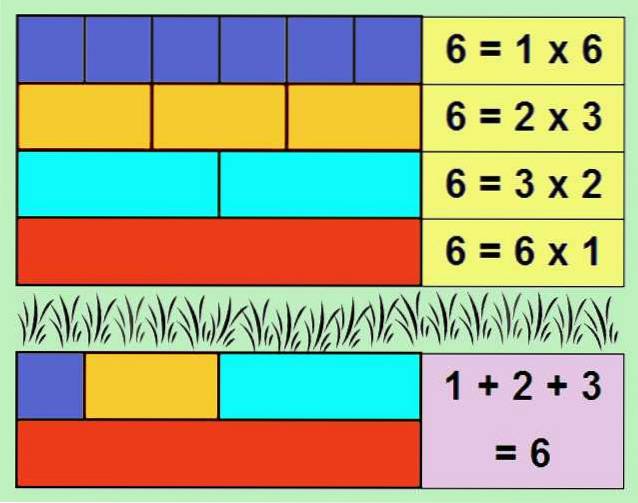
Eines der einfachsten Beispiele für eine perfekte Zahl ist 6, da ihre Teiler 1, 2 und 3 sind. Wenn wir die Teiler addieren, erhalten wir: 1 + 2 + 3 = 6.
Die Summe der Teiler einer ganzen Zahl ohne die Zahl selbst wird aufgerufen Aliquot. Daher ist eine perfekte Zahl gleich ihrem Aliquot.
Wenn jedoch die Zahl selbst in der Summe der Teiler einer Zahl enthalten ist, ist eine perfekte Zahl eine, bei der die Summe aller durch 2 geteilten Teiler gleich der Zahl selbst ist..
Artikelverzeichnis
Mathematiker der Antike, insbesondere die Griechen, legten großen Wert auf perfekte Zahlen und schrieben ihnen göttliche Eigenschaften zu..
Zum Beispiel bestätigte Philo von Alexandria gegen das erste Jahrhundert, dass 6 und 28 perfekte Zahlen sind, die mit den sechs Tagen der Erschaffung der Welt und den achtundzwanzig Tagen zusammenfallen, die der Mond benötigt, um die Erde zu umrunden..
Perfekte Zahlen sind auch in der Natur vorhanden, zum Beispiel erscheint am Nordpol des Saturn auch die perfekte Zahl 6, ein sechseckiger Wirbel, der von der Cassini-Sonde gefunden wurde und der Wissenschaftler fasziniert hat..
Die Bienenwaben haben Zellen in sechseckiger Form, dh mit 6 Seiten. Es wurde gezeigt, dass das Polygon mit der perfekten Zahl 6 dasjenige ist, das es ermöglicht, die Anzahl der Zellen im Bienenstock mit dem Minimum an Wachs für seine Ausarbeitung zu maximieren..
Die Summe aller Teiler einer natürlichen Zahl n wird mit σ (n) bezeichnet. In einer perfekten Zahl ist erfüllt, dass: σ (n) = 2n.
Euklid entdeckte eine Formel und ein Kriterium, mit denen die perfekten Zahlen gefunden werden können. Diese Formel lautet:
zwei(n-1) (zwein -1)
Die durch die Formel erzeugte Zahl ist jedoch nur dann perfekt, wenn der Faktor (2n -1) sei ein Cousin.
Mal sehen, wie die ersten perfekten Zahlen erzeugt werden:
Wenn n = 2 ist, bleibt uns 2 übrig1 (zweizwei - 1) = 2 x 3 = 6, was wir bereits gesehen haben, ist perfekt.
Wenn n = 3 ist, haben wir 2zwei (zwei3 - 1) = 4 x 7 = 28, was auch perfekt ist, wie in Beispiel 1 im Detail verifiziert.
Mal sehen, was mit n = 4 passiert. Beim Ersetzen in Euklids Formel haben wir:
zwei3 (zwei4 - 1) = 8 x 15 = 120
Es kann überprüft werden, dass diese Zahl nicht perfekt ist, wie in Beispiel 3 ausführlich gezeigt. Dies widerspricht nicht dem Euklid-Kriterium, da 15 keine Primzahl ist, eine notwendige Voraussetzung dafür, dass das Ergebnis eine perfekte Zahl ist.
Nun wollen wir sehen, was passiert, wenn n = 5 ist. Anwendung der Formel, die wir haben:
zwei4 (zwei5 - 1) = 16 x 31 = 496
Da 31 eine Primzahl ist, muss die Zahl 496 nach Euklids Kriterien perfekt sein. In Beispiel 4 wird detailliert gezeigt, dass dies tatsächlich der Fall ist.
Primzahlen, die die Form 2 habenp - Ich werde Mersenne-Cousins genannt, nach dem Mönch Marin Mersenne, der bereits im 17. Jahrhundert Primzahlen und perfekte Zahlen studierte..
Später im 18. Jahrhundert zeigte Leonhard Euler, dass alle perfekten Zahlen, die durch Euklids Formel erzeugt werden, gerade sind.
Bisher wurde kein perfektes Perfekt gefunden.
Bis heute sind 51 perfekte Zahlen bekannt, die alle nach der Formel und dem Euklid-Kriterium erzeugt werden. Diese Zahl wurde erhalten, sobald der größere Cousin von Mersenne gefunden wurde, nämlich: (282589933 - 1).
Die perfekte Nummer # 51 ist (282589933) x (282589933 - 1) und hat 49724095 Ziffern.
In der Zahlentheorie heißt es, dass zwei Zahlen Freunde sind, wenn die Summe der Teiler einer Zahl ohne die Zahl selbst gleich der anderen Zahl ist und umgekehrt.
Der Leser kann überprüfen, ob die Summe der Teiler von 220 ohne 220 284 beträgt. Andererseits ist die Summe der Teiler von 284 ohne 284 gleich 220. Daher ist das Zahlenpaar 220 und 284 Freunde.
Unter diesem Gesichtspunkt ist eine perfekte Zahl mit sich selbst befreundet..
Die ersten acht perfekten Zahlen sind unten aufgeführt:
6
28
496
8128
33550336
8589869056
137438691328
2305843008139952128
In den folgenden Übungen müssen die Teiler einer Zahl berechnet, dann addiert und überprüft werden, ob die Zahl eine perfekte Zahl ist oder nicht..
Bevor wir uns den Übungen nähern, werden wir daher das Konzept überprüfen und zeigen, wie sie berechnet werden..
Zunächst muss man bedenken, dass Zahlen Primzahlen (wenn sie nur genau mit sich selbst und 1 geteilt werden können) oder zusammengesetzt (wenn sie als Produkt von Primzahlen zerlegt werden können) sein können..
Für eine zusammengesetzte Zahl N haben wir:
N = an . bm. cp ... rk
Wobei a, b, c… r Primzahlen sind und n, m, p… k Exponenten sind, die zu den natürlichen Zahlen gehören, die ab 1 sein können.
In Bezug auf diese Exponenten gibt es eine Formel, um zu wissen, wie viele Teiler die Zahl N hat, obwohl sie uns nicht sagt, was diese sind. Sei C diese Größe, dann:
C = (n + 1) (m + 1) (p + 1)… (k + 1)
Wenn wir die Zahl N als Produkt von Primzahlen zerlegen und wissen, wie viele Teiler sie hat, sowohl Primzahlen als auch Nicht-Primzahlen, können wir bestimmen, was diese Teiler sind..
Sobald Sie alle haben, mit Ausnahme der letzten, die in der Summe nicht benötigt wird, können Sie überprüfen, ob es sich um eine perfekte Zahl handelt oder nicht.
Stellen Sie sicher, dass die Nummer 28 perfekt ist.
Das erste wird sein, die Zahl in ihre Primfaktoren zu zerlegen.
28 | 2
14 | 2
07 | 7
01 | 1
Seine Teiler sind: 1, 2, 4, 7, 14 und 28. Wenn wir 28 ausschließen, ergibt die Summe der Teiler:
1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28
Daher ist 28 eine perfekte Zahl.
Weiterhin ist die Summe aller seiner Teiler 28 + 28, so dass die Regel σ (28) = 2 x 28 erfüllt ist.
Entscheiden, ob die Zahl 38 perfekt ist oder nicht.
Die Zahl wird in ihre Primfaktoren zerlegt:
39 | 3
13 | 13
01 | 1
Die Teiler von 39 ohne Angabe der Zahl selbst sind: 1, 3 und 13. Die Summe 1 + 3 + 13 = 4 + 13 = 17 ist nicht gleich 39, daher ist 39 eine unvollständige oder nicht perfekte Zahl.
Finden Sie heraus, ob Engel Nummer 120 perfekt oder unvollkommen ist.
Wir zerlegen die Zahl in ihre Primfaktoren:
120 | 2
060 | 2
30 | 2
15 | 3
5 | 5
1 | 1
Aus den Primfaktoren finden wir die Teiler:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 und 120
Wenn 120 perfekt wäre, sollte das Hinzufügen aller Teiler 2 x 120 = 240 ergeben.
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360
Dieses Ergebnis unterscheidet sich deutlich von 240, so dass der Schluss gezogen wird, dass die Zahl 120 keine perfekte Zahl ist..
Stellen Sie sicher, dass die nach Euklids Kriterium erhaltene Zahl 496 eine perfekte Zahl ist.
Die Zahl 496 wird in ihre Primfaktoren zerlegt:
496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1
Die Teiler sind also:
1, 2, 4, 8, 16, 31, 62, 124, 248, 496
Jetzt werden alle hinzugefügt, außer 496:
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Bestätigung, dass es sich tatsächlich um eine perfekte Zahl handelt.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.