
Nullwinkel Definition und Eigenschaften, Beispiele, Übungen
Das Nullwinkel Es ist eines, dessen Maß 0 ist, sowohl in Grad als auch im Bogenmaß oder einem anderen System zur Winkelmessung. Daher fehlt es an Breite oder Öffnung, wie sie beispielsweise zwischen zwei parallelen Linien gebildet wird..
Obwohl seine Definition einfach genug klingt, ist der Nullwinkel in vielen physikalischen und technischen Anwendungen sowie in der Navigation und im Design sehr nützlich..
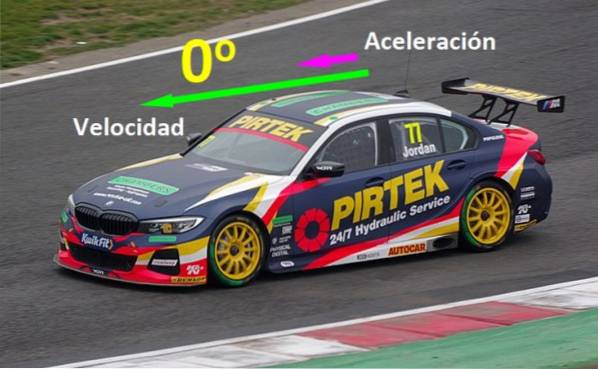
Es gibt physikalische Größen, die parallel ausgerichtet werden müssen, um bestimmte Effekte zu erzielen: Wenn sich ein Auto auf einer Autobahn in einer geraden Linie bewegt und seinen Geschwindigkeitsvektor eingibt v und sein Beschleunigungsvektor zu es gibt 0º, das Auto bewegt sich schneller und schneller, aber wenn das Auto bremst, ist seine Beschleunigung entgegengesetzt zu seiner Geschwindigkeit (siehe Abbildung 1).
Die folgende Abbildung zeigt verschiedene Winkeltypen, einschließlich des Nullwinkels rechts. Wie zu sehen ist, fehlt dem 0º-Winkel die Breite oder Öffnung..

Artikelverzeichnis
- 1 Beispiele für Nullwinkel
- 1.1 - Auswirkungen des Nullwinkels auf physikalische Größen
- 2 Übungen
- 2.1 - Übung 1
- 2.2 - Übung 2
- 3 Referenzen
Beispiele für Nullwinkel
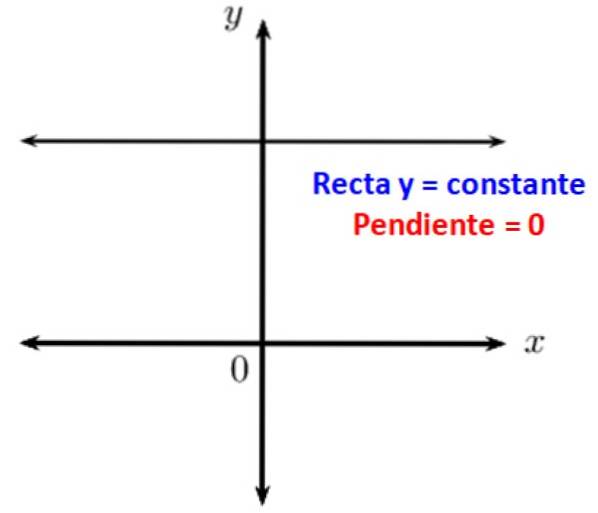
Es ist bekannt, dass parallele Linien miteinander einen Nullwinkel bilden. Wenn Sie eine horizontale Linie haben, verläuft diese parallel zur x-Achse des kartesischen Koordinatensystems, daher beträgt ihre Neigung dazu 0. Mit anderen Worten, horizontale Linien haben eine Steigung von Null.
Auch die trigonometrischen Verhältnisse des Nullwinkels sind 0, 1 oder unendlich. Daher ist der Nullwinkel in vielen physikalischen Situationen vorhanden, die Operationen mit Vektoren beinhalten. Diese Gründe sind:
-sin 0º = 0
-cos 0º = 1
-tg 0º = 0
-sec 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
Und sie werden nützlich sein, um einige Beispiele für Situationen zu analysieren, in denen das Vorhandensein des Nullwinkels eine grundlegende Rolle spielt:
- Auswirkungen des Nullwinkels auf physikalische Größen
Vektoraddition
Wenn zwei Vektoren parallel sind, ist der Winkel zwischen ihnen Null, wie in 4a oben gezeigt. In diesem Fall wird die Summe von beiden durch Platzieren nacheinander ausgeführt, und die Größe des Summenvektors ist die Summe der Größen der Addenden (Abbildung 4b)..

Wenn zwei Vektoren parallel sind, ist der Winkel zwischen ihnen Null, wie in 4a oben gezeigt. In diesem Fall wird die Summe von beiden durch Platzieren nacheinander ausgeführt, und die Größe des Summenvektors ist die Summe der Größen der Addenden (Abbildung 4b).
Das Drehmoment oder Drehmoment
Das Drehmoment oder Drehmoment bewirkt die Drehung eines Körpers. Dies hängt von der Größe der ausgeübten Kraft und ihrer Anwendung ab. Ein sehr repräsentatives Beispiel ist der Schraubenschlüssel in der Abbildung.
Um den besten Dreheffekt zu erzielen, wird die Kraft senkrecht zum Schraubenschlüsselgriff nach oben oder unten ausgeübt. Es wird jedoch keine Drehung erwartet, wenn die Kraft parallel zum Griff ist..
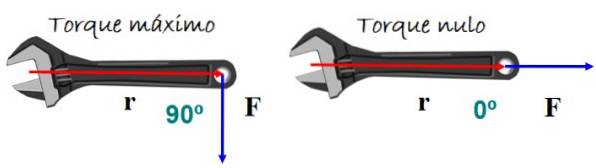
Mathematisch Drehmoment τ ist definiert als das Kreuzprodukt oder Kreuzprodukt zwischen Vektoren r (Positionsvektor) und F. (Kraftvektor) aus Abbildung 5:
τ = r x F.
Die Größe des Drehmoments ist:
τ = r F sin θ
Wobei θ der Winkel zwischen ist r Y. F.. Wenn sin θ = 0 ist, ist das Drehmoment Null, in diesem Fall ist θ = 0º (oder auch 180º).
Elektrischer Feldfluss
Der elektrische Feldfluss ist eine skalare Größe, die von der Intensität des elektrischen Feldes sowie von der Ausrichtung der Oberfläche abhängt, durch die es verläuft..
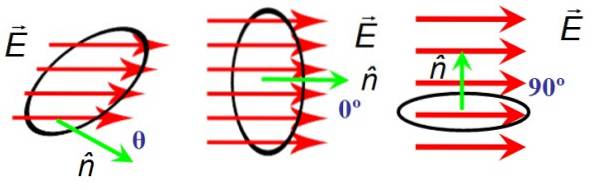
In 6 gibt es eine kreisförmige Fläche des Bereichs A, durch die die elektrischen Feldlinien verlaufen UND. Die Ausrichtung der Oberfläche ist durch den Normalenvektor gegeben n. Links bilden das Feld und der Normalenvektor einen beliebigen spitzen Winkel θ, in der Mitte bilden sie einen Nullwinkel miteinander und rechts stehen sie senkrecht.
Wann UND Y. n senkrecht sind, kreuzen die Feldlinien nicht die Oberfläche und daher ist der Fluss Null, während wenn der Winkel zwischen UND Y. n ist null, durchlaufen die Linien die Oberfläche vollständig.
Die Definition des elektrischen Feldflusses durch den griechischen Buchstaben Φ (lesen Sie „fi“), seine Definition für ein einheitliches Feld wie in der Abbildung, sieht folgendermaßen aus:
Φ = UND• •nZU
Der Punkt in der Mitte beider Vektoren bezeichnet das Punktprodukt oder Punktprodukt, das alternativ wie folgt definiert ist:
Φ = UND• •nA = EAcosθ
Das Fett und die Pfeile über dem Buchstaben sind Mittel zur Unterscheidung zwischen einem Vektor und seiner Größe, die durch normale Buchstaben gekennzeichnet ist. Da cos 0 = 1 ist, ist der Fluss maximal, wenn UND Y. n sie sind parallel.
Ausbildung
- Übung 1
Zwei Kräfte P. Y. Q. wirken gleichzeitig auf ein Punktobjekt X, bilden beide Kräfte zunächst einen Winkel θ zwischen ihnen. Was passiert mit der Größe der resultierenden Kraft, wenn θ auf Null abfällt??
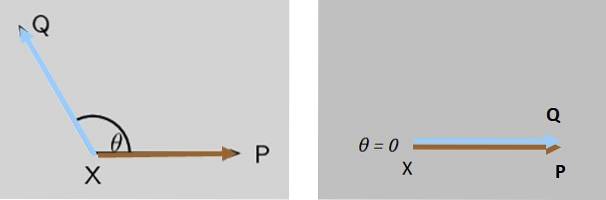
Lösung
Die Größe der resultierenden Kraft Q. + P. steigt allmählich an, bis es maximal ist, wenn Q. Y. P. sind völlig parallel (Abbildung 7 rechts).
- Übung 2
Geben Sie an, ob der Nullwinkel eine Lösung der folgenden trigonometrischen Gleichung ist:
cos 2x = 1 + 4 sin x
Lösung
Eine trigonometrische Gleichung ist eine Gleichung, bei der das Unbekannte Teil des Arguments eines trigonometrischen Verhältnisses ist. Um die vorgeschlagene Gleichung zu lösen, ist es zweckmäßig, die Formel für den Kosinus des Doppelwinkels zu verwenden:
cos 2x = coszwei x - Sündezwei x
Denn auf diese Weise wird das Argument auf der linken Seite x Anstatt von 2x. Dann:
coszwei x - Sündezwei x = 1 + 4sin x
Auf der anderen Seite coszwei x + sinzwei x = 1, also:
coszwei x - Sündezwei x = coszwei x + sinzwei x + 4sen x
Der Begriff coszwei x wird abgebrochen und bleibt:
- senzwei x = Sündezwei x + 4sen x → - 2senzwei x - 4senx = 0 → 2senzwei x + 4senx = 0
Nun wird die folgende Variablenänderung vorgenommen: sinx = u und die Gleichung wird:
2uzwei + 4u = 0
2u (u + 4) = 0
Wessen Lösungen sind: u = 0 und u = -4. Wenn wir die Änderung zurückgeben, haben wir zwei Möglichkeiten: sin x = 0 und sinx = -4. Diese letzte Lösung ist nicht realisierbar, da der Sinus eines beliebigen Winkels zwischen -1 und 1 liegt. Wir haben also die erste Alternative:
sin x = 0
Daher ist x = 0º eine Lösung, aber jeder Winkel, dessen Sinus 0 ist, funktioniert auch, der auch 180º (π Radiant), 360º (2 π Radiant) und die jeweiligen Negative sein kann.
Die allgemeinste Lösung der trigonometrischen Gleichung lautet: x = kπ wobei k = 0, ± 1, ± 2, ± 3,…. k eine ganze Zahl.
Verweise
- Baldor, A. 2004. Ebenen- und Raumgeometrie mit Trigonometrie. Publicaciones Cultural S.A. de C.V. Mexiko.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 3. Partikelsysteme. Herausgegeben von Douglas Figueroa (USB).
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 5. Elektrische Wechselwirkung. Herausgegeben von Douglas Figueroa (USB).
- OnlineMathLearning. Arten von Winkeln. Wiederhergestellt von: onlinemathlearning.com.
- Zill, D. 2012. Algebra, Trigonometrie und analytische Geometrie. McGraw Hill Interamericana.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.