Das Einheitszelle Es ist ein imaginärer Raum oder eine imaginäre Region, die den minimalen Ausdruck eines Ganzen darstellt; dass im Falle der Chemie das Ganze ein Kristall wäre, der aus Atomen, Ionen oder Molekülen besteht, die nach einem Strukturmuster angeordnet sind.
Beispiele finden sich im Alltag, die dieses Konzept verkörpern. Dazu ist es notwendig, auf Objekte oder Oberflächen zu achten, die eine bestimmte sich wiederholende Reihenfolge ihrer Elemente aufweisen. Einige Mosaike, Basreliefs, Kassettendecken, Blätter und Tapeten können allgemein das umfassen, was unter Einheitszelle zu verstehen ist.
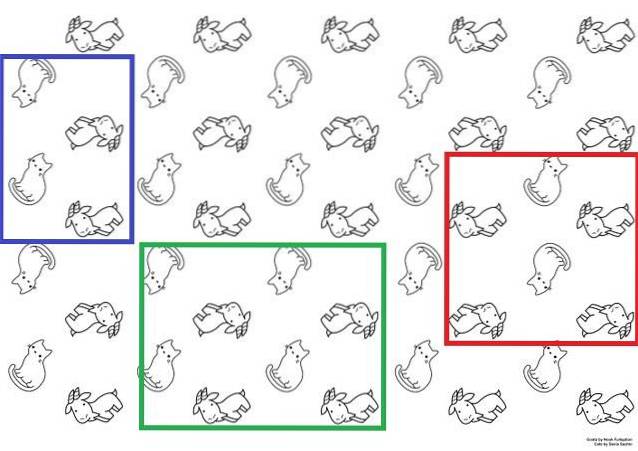
Zur besseren Veranschaulichung gibt es das Bild oben, das als Hintergrundbild verwendet werden könnte. Darin erscheinen Katzen und Ziegen mit zwei alternativen Sinnen; Katzen stehen aufrecht oder auf dem Kopf und Ziegen liegen mit dem Gesicht nach oben oder unten.
Diese Katzen und Ziegen bilden eine sich wiederholende Struktursequenz. Um das gesamte Papier aufzubauen, würde es ausreichen, die Einheitszelle mit translatorischen Bewegungen ausreichend oft über der Oberfläche zu reproduzieren..
Mögliche Einheitszellen werden durch die blauen, grünen und roten Kästchen dargestellt. Jeder dieser drei könnte verwendet werden, um die Rolle zu erhalten; Es ist jedoch notwendig, sie einfallsreich entlang der Oberfläche zu bewegen, um herauszufinden, ob sie dieselbe im Bild beobachtete Sequenz reproduzieren.
Beginnend mit dem roten Kästchen wäre es wünschenswert, wenn drei Spalten (von Katzen und Ziegen) nach links verschoben würden, zwei Ziegen nicht mehr unten erscheinen würden, sondern nur noch eine. Daher würde es zu einer anderen Sequenz führen und kann nicht als Einheitszelle betrachtet werden.
Wenn sie dagegen die beiden Kästchen blau und grün einfallsreich bewegen würden, würde die gleiche Reihenfolge des Papiers erhalten. Beide sind Einheitszellen; Das blaue Kästchen folgt jedoch mehr der Definition, da es kleiner als das grüne Kästchen ist.
Artikelverzeichnis
Die eigene Definition verdeutlicht zusätzlich zu dem gerade erläuterten Beispiel einige seiner Eigenschaften:
-Wenn Sie sich unabhängig von der Richtung im Raum bewegen, erhalten Sie den vollständigen Körper oder Kristall. Dies liegt daran, dass sie, wie bei Katzen und Ziegen erwähnt, die strukturelle Abfolge reproduzieren; das ist gleich der räumlichen Verteilung der sich wiederholenden Einheiten.
-Sie müssen im Vergleich zu anderen möglichen Zellenoptionen so klein wie möglich sein (oder wenig Volumen einnehmen).
-Sie sind normalerweise symmetrisch. Auch seine Symmetrie spiegelt sich buchstäblich in den Kristallen der Verbindung wider; Wenn die Elementarzelle eines Salzes kubisch ist, sind seine Kristalle kubisch. Es gibt jedoch kristalline Strukturen, die mit Elementarzellen mit verzerrten Geometrien beschrieben werden..
-Sie enthalten sich wiederholende Einheiten, die durch Punkte ersetzt werden können, die wiederum ein sogenanntes Gitter in drei Dimensionen bilden. Im vorherigen Beispiel stellen die Katzen und Ziegen die Gitterpunkte dar, von einer höheren Ebene aus gesehen. das heißt, zwei Dimensionen.
Die sich wiederholenden Einheiten oder Gitterpunkte der Einheitszellen behalten den gleichen Anteil der festen Teilchen bei.
Wenn Sie die Anzahl der Katzen und Ziegen in der blauen Box zählen, haben Sie zwei Katzen und Ziegen. Das gleiche passiert mit der grünen Box und auch mit der roten Box (auch wenn bereits bekannt ist, dass es sich nicht um eine Einheitszelle handelt)..
Nehmen wir zum Beispiel an, dass Katzen und Ziegen G- bzw. C-Atome sind (eine seltsame Tierschweißnaht). Da das Verhältnis von G zu C in der blauen Box 2: 2 oder 1: 1 beträgt, kann mit Sicherheit erwartet werden, dass der Feststoff die Formel GC (oder CG) hat..
Wenn der Feststoff mehr oder weniger kompakte Strukturen aufweist, wie dies bei Salzen, Metallen, Oxiden, Sulfiden und Legierungen der Fall ist, gibt es in den Einheitszellen keine ganzen sich wiederholenden Einheiten; Das heißt, es gibt Teile oder Teile davon, die sich zu einer oder zwei Einheiten addieren.
Dies ist bei GC nicht der Fall. In diesem Fall würde die blaue Box die Katzen und Ziegen in zwei (1 / 2G und 1 / 2C) oder vier (1 / 4G und 1 / 4C) „aufteilen“. In den nächsten Abschnitten wird ersichtlich, dass in diesen Einheitszellen die retikulären Punkte auf diese und andere Weise zweckmäßigerweise unterteilt sind..
Die Einheitszellen im GC-Beispiel sind zweidimensional; Dies gilt jedoch nicht für reale Modelle, die alle drei Dimensionen berücksichtigen. Somit werden die Quadrate oder Parallelogramme in Parallelepipeds umgewandelt. Nun macht der Begriff "Zelle" mehr Sinn.
Die Abmessungen dieser Zellen oder Parallelepipeds hängen davon ab, wie lang ihre jeweiligen Seiten und Winkel sind..
Im unteren Bild haben Sie die untere hintere Ecke des Parallelepipeds, die aus den Seiten besteht zu, b Y. c, und die Winkel α, β und γ.
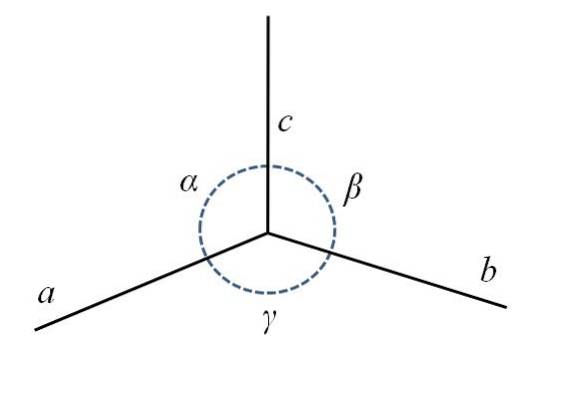
Wie du siehst, zu ist etwas länger als b Y. c. In der Mitte befindet sich ein gepunkteter Kreis, um die Winkel α, β und γ zwischen anzuzeigen ac, cb Y. ba, beziehungsweise. Für jede Einheitszelle haben diese Parameter konstante Werte und definieren ihre Symmetrie und die des restlichen Kristalls..
Wenn man wieder etwas Fantasie anwendet, definieren die Bildparameter eine würfelförmige Zelle, die an ihrem Rand ausgestreckt ist. zu. Somit entstehen Einheitszellen mit unterschiedlichen Längen und Winkeln ihrer Kanten, die auch in verschiedene Typen eingeteilt werden können.
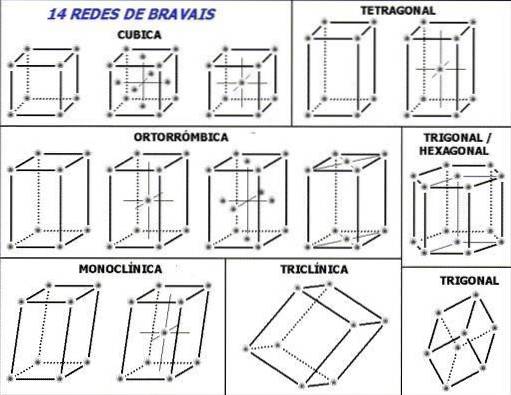
Beachten Sie zunächst im oberen Bild die gepunkteten Linien innerhalb der Einheitszellen: Sie geben den unteren hinteren Winkel an, wie gerade erläutert. Die folgende Frage kann gestellt werden: Wo sind die Gitterpunkte oder sich wiederholenden Einheiten? Obwohl sie den falschen Eindruck erwecken, dass die Zellen leer sind, liegt die Antwort an ihren Eckpunkten.
Diese Zellen werden so erzeugt oder ausgewählt, dass sich die sich wiederholenden Einheiten (graue Punkte des Bildes) an ihren Eckpunkten befinden. Abhängig von den Werten der im vorherigen Abschnitt festgelegten Parameter, die für jede Einheitszelle konstant sind, werden sieben Kristallsysteme abgeleitet.
Jedes Kristallsystem hat eine eigene Einheitszelle; der zweite definiert den ersten. Im oberen Bild gibt es sieben Quadrate, die den sieben Kristallsystemen entsprechen; oder etwas zusammengefasster kristalline Netzwerke. So entspricht beispielsweise eine kubische Einheitszelle einem der Kristallsysteme, die ein kubisches Kristallgitter definieren.
Dem Bild zufolge sind die kristallinen Systeme oder Netzwerke:
-Kubisch
-Tetragonal
-Orthorhombisch
-Sechseckig
-Monoklin
-Triklinisch
-Trigonal
Und innerhalb dieser kristallinen Systeme entstehen andere, die die vierzehn Bravais-Netzwerke bilden; dass sie unter allen kristallinen Netzwerken die grundlegendsten sind.
In einem Würfel sind alle Seiten und Winkel gleich. Daher gilt in dieser Einheitszelle Folgendes:
zu = b = c
α = β = γ = 90º
Es gibt drei kubische Einheitszellen: einfach oder primitiv, körperzentriert (bcc) und flächenzentriert (fcc). Die Unterschiede liegen in der Verteilung der Punkte (Atome, Ionen oder Moleküle) und in ihrer Anzahl.
Welche dieser Zellen ist die kompakteste? Derjenige, dessen Volumen mehr von Punkten besetzt ist: der kubische, der auf den Gesichtern zentriert ist. Beachten Sie, dass wenn wir die Punkte für Katzen und Ziegen von Anfang an ersetzen würden, sie nicht auf eine einzelne Zelle beschränkt wären. Sie würden gehören und von mehreren geteilt werden. Wieder wären es Teile von G oder C..
Wenn Katzen oder Ziegen an den Eckpunkten wären, würden sie von 8 Einheitszellen geteilt; Das heißt, jede Zelle hätte 1/8 von G oder C. Verbinden oder stellen Sie sich 8 Würfel in zwei Spalten mit jeweils zwei Zeilen vor, um sie zu visualisieren.
Wenn Katzen oder Ziegen auf den Gesichtern wären, würden sie nur von 2 Einheitszellen geteilt. Um es zu sehen, setzen Sie einfach zwei Würfel zusammen.
Wenn andererseits die Katze oder die Ziege in der Mitte des Würfels wären, würden sie nur zu einer einzelnen Einheitszelle gehören; Das gleiche passiert mit den Feldern im Hauptbild, als das Konzept angesprochen wurde.
Sagte dann das Obige, innerhalb einer einfachen kubischen Einheitszelle, die wir haben ein Einheit oder Gitterpunkt, da er 8 Eckpunkte hat (1/8 x 8 = 1). Für die im Körper zentrierte kubische Zelle gibt es: 8 Eckpunkte, die einem Atom entsprechen, und einen Punkt oder eine Einheit in der Mitte; deshalb gibt es zwei Einheiten.
Und für die flächenzentrierte kubische Zelle gibt es: 8 Eckpunkte (1) und sechs Flächen, wobei die Hälfte jedes Punktes oder jeder Einheit geteilt wird (1/2 x 6 = 3); deshalb besitzt es vier Einheiten.
Ähnliche Kommentare können bezüglich der Einheitszelle für das tetragonale System abgegeben werden. Seine strukturellen Parameter sind die folgenden:
zu = b ≠ c
α = β = γ = 90º
Die Parameter für die orthorhombische Zelle sind:
zu ≠ b ≠ c
α = β = γ = 90º
Die Parameter für die monokline Zelle sind:
zu ≠ b ≠ c
α = γ = 90 °; β ≠ 90º
Die Parameter für die trikline Zelle sind:
zu ≠ b ≠ c
α ≠ β ≠ γ ≠ 90º
Die Parameter für die hexagonale Zelle sind:
zu = b ≠ c
α = β = 90 °; γ ≠ 120º
Tatsächlich bildet die Zelle ein Drittel eines hexagonalen Prismas.
Und schließlich sind die Parameter für die trigonale Zelle:
zu = b = c
α = β = γ ≠ 90º
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.