Heisenberg-Atommodell

Was ist Heisenbergs Atommodell??

Das Heisenberg-Atommodell (1927) führt das Unsicherheitsprinzip in die den Atomkern umgebenden Elektronenorbitale ein. Der bekannte deutsche Physiker legte den Grundstein für die Quantenmechanik, um das Verhalten der subatomaren Teilchen, aus denen ein Atom besteht, abzuschätzen.

Das Unsicherheitsprinzip von Werner Heisenberg zeigt, dass es nicht möglich ist, die Position und den linearen Impuls eines Elektrons gleichzeitig mit Sicherheit zu kennen. Das gleiche Prinzip gilt für die Variablen Zeit und Energie; Das heißt, wenn wir eine Ahnung von der Position des Elektrons haben, kennen wir den linearen Impuls des Elektrons nicht und umgekehrt.

Kurz gesagt, es ist nicht möglich, den Wert beider Variablen gleichzeitig vorherzusagen. Das Vorstehende bedeutet nicht, dass eine der vorgenannten Größen nicht genau bekannt sein kann. Solange es separat ist, gibt es kein Hindernis, um den Zinswert zu erhalten.

Unsicherheit tritt jedoch auf, wenn zwei konjugierte Größen wie Position und linearer Impuls sowie Zeit zusammen mit Energie gleichzeitig erkannt werden sollen..

Dieses Prinzip ergibt sich aus einer streng theoretischen Argumentation als einzig brauchbare Erklärung für wissenschaftliche Beobachtungen.

Eigenschaften des Heisenberg-Atommodells

Im März 1927 veröffentlichte Heisenberg seine Arbeit Zum Wahrnehmungsgehalt von Kinematik und quantentheoretischer Mechanik, wo Sie das Unsicherheits- oder Unbestimmtheitsprinzip detailliert beschrieben haben.

Dieses Prinzip, das im von Heisenberg vorgeschlagenen Atommodell von grundlegender Bedeutung ist, zeichnet sich durch Folgendes aus:

• Das Unsicherheitsprinzip ergibt sich aus einer Erklärung, die die neuen Atomtheorien über das Verhalten von Elektronen ergänzt. Trotz der Verwendung von Messgeräten mit hoher Präzision und Empfindlichkeit ist in jedem experimentellen Test immer noch Unbestimmtheit vorhanden.
• Aufgrund des Unsicherheitsprinzips wird bei der Analyse zweier verwandter Variablen die Unsicherheit über den Wert der anderen Variablen immer größer, wenn Sie eine dieser Variablen genau kennen..
• Der Impuls und die Position eines Elektrons oder eines anderen subatomaren Teilchens können nicht gleichzeitig gemessen werden.
• Die Beziehung zwischen beiden Variablen ist durch eine Ungleichung gegeben. Nach Heisenberg ist das Produkt der Variationen des linearen Impulses und der Position des Teilchens immer größer als der Quotient zwischen der Plankenkonstante (6.62606957 (29) × 10) ^{-3. 4} Jules x Sekunden) und 4π, wie im folgenden mathematischen Ausdruck beschrieben:

Die diesem Ausdruck entsprechende Legende lautet wie folgt:

∆p: Unbestimmtheit des linearen Moments.

∆x: Unbestimmtheit der Position.

h: Plankenkonstante.

π: Zahl pi 3.14.

• In Anbetracht des Vorstehenden hat das Produkt der Unsicherheiten als Untergrenze das Verhältnis h / 4π, das ein konstanter Wert ist. Wenn daher eine der Größen gegen Null tendiert, muss die andere im gleichen Verhältnis zunehmen.
• Diese Beziehung gilt für alle Paare konjugierter kanonischer Größen. Zum Beispiel: Das Heisenbergsche Unsicherheitsprinzip ist perfekt auf das Energie-Zeit-Paar anwendbar, wie unten beschrieben:

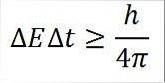
In diesem Ausdruck:

∆E: Unbestimmtheit der Energie.

∆t: Unbestimmtheit der Zeit.

h: Plankenkonstante.

π: Zahl pi 3.14.

• Aus diesem Modell folgt, dass ein absoluter kausaler Determinismus in konjugierten kanonischen Variablen unmöglich ist, da man, um diese Beziehung herzustellen, Kenntnisse über die Anfangswerte der Studienvariablen haben sollte.
• Folglich basiert das Heisenberg-Modell aufgrund der Zufälligkeit, die zwischen den Variablen auf subatomaren Ebenen besteht, auf probabilistischen Formulierungen..

Experimentelle Tests

Das Heisenbergsche Unsicherheitsprinzip ist die einzig mögliche Erklärung für die experimentellen Tests, die in den ersten drei Jahrzehnten des 21. Jahrhunderts durchgeführt wurden..

Bevor Heisenberg das Unsicherheitsprinzip aussprach, deuteten die damals geltenden Vorschriften darauf hin, dass die Variablen linearer Impuls, Position, Drehimpuls, Zeit, Energie unter anderem für subatomare Teilchen operativ definiert wurden.

Dies bedeutete, dass sie so behandelt wurden, als wären sie klassische Physik; Das heißt, ein Anfangswert wurde gemessen und der Endwert wurde gemäß dem vorher festgelegten Verfahren geschätzt.

Dies implizierte die Definition eines Referenzsystems für Messungen, des Messinstruments und der Art und Weise der Verwendung dieses Instruments gemäß der wissenschaftlichen Methode..

Dementsprechend mussten sich die von subatomaren Partikeln beschriebenen Variablen deterministisch verhalten. Das heißt, sein Verhalten musste genau und präzise vorhergesagt werden..

Jedes Mal, wenn ein Test dieser Art durchgeführt wurde, war es jedoch unmöglich, den theoretisch geschätzten Wert in der Messung zu erhalten.. 

Die Messungen waren aufgrund der natürlichen Bedingungen des Experiments verzerrt, und das erhaltene Ergebnis war nicht nützlich, um die Atomtheorie anzureichern.

Beispiel

Zum Beispiel: Wenn es darum geht, die Geschwindigkeit und Position eines Elektrons zu messen, muss der Versuchsaufbau die Kollision eines Lichtphotons mit dem Elektron berücksichtigen.

Diese Kollision induziert eine Variation der Geschwindigkeit und der intrinsischen Position des Elektrons, mit der das Messobjekt durch die experimentellen Bedingungen verändert wird..

Daher ermutigt der Forscher das Auftreten eines unvermeidbaren experimentellen Fehlers trotz der Genauigkeit und Präzision der verwendeten Instrumente..

Andere Quantenmechanik als die klassische Mechanik

Darüber hinaus besagt das Unbestimmtheitsprinzip von Heisenberg, dass die Quantenmechanik per Definition anders funktioniert als die klassische Mechanik.

Folglich wird angenommen, dass die genaue Kenntnis der Messungen auf subatomarer Ebene durch die feine Linie zwischen klassischer und Quantenmechanik begrenzt ist..

Einschränkungen des Heisenberg-Modells

Trotz der Erklärung der Unbestimmtheit subatomarer Teilchen und der Feststellung der Unterschiede zwischen klassischer und Quantenmechanik stellt Heisenbergs Atommodell keine einzige Gleichung auf, um die Zufälligkeit dieser Art von Phänomenen zu erklären..

Darüber hinaus impliziert die Tatsache, dass die Beziehung durch eine Ungleichung hergestellt wird, dass der Bereich der Möglichkeiten für das Produkt zweier konjugierter kanonischer Variablen unbestimmt ist. Folglich ist die Unsicherheit, die subatomaren Prozessen innewohnt, signifikant..

Artikel von Interesse

Schrödingers Atommodell.

Atomic de Broglie Modell.

Chadwick-Atommodell.

Perrins Atommodell.

Thomsons Atommodell.

Dalton-Atommodell.

Dirac Jordan Atommodell.

Atommodell von Demokrit.

Atommodell von Leukipp.

Bohr-Atommodell.

Sommerfeld-Atommodell.

Aktuelles Atommodell.

Verweise

1. Beyler, R. (1998). Werner Heisenberg. Encyclopædia Britannica, Inc. Wiederhergestellt von: britannica.com
2. Das Heisenbergsche Unsicherheitsprinzip (s.f.). Wiederhergestellt von: hiru.eus
3. García, J. (2012). Heisenbergs Unsicherheitsprinzip. Wiederhergestellt von: hiberus.com
4. Atommodelle (s.f.). Nationale Autonome Universität von Mexiko. Mexiko DF, Mexiko. Wiederhergestellt von: asesorias.cuautitlan2.unam.mx
5. Werner Heisenberg (s.f.). Erholt von: the-history-of-the-atom.wikispaces.com
6. Wikipedia, die freie Enzyklopädie (2018). Plank ist konstant. Wiederhergestellt von: es.wikipedia.org
7. Wikipedia, die freie Enzyklopädie (2018). Heisenbergs Unbestimmtheitsrelation. Wiederhergestellt von: es.wikipedia.org