
Gaußsches Gesetz

Was ist das Gaußsche Gesetz??
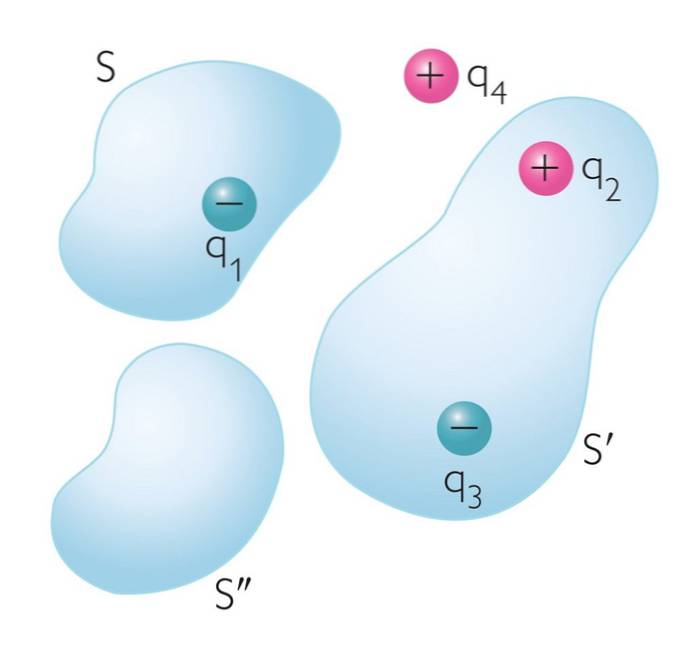
Das Gaußsches Gesetz stellt fest, dass der elektrische Feldfluss durch eine imaginäre geschlossene Oberfläche proportional zum Nettoladungswert der Partikel ist, die sich in der Oberfläche befinden.
Bezeichnung des elektrischen Flusses durch eine geschlossene Fläche als ΦUND und die von der Oberfläche eingeschlossene Nettoladung durch Q.enc, dann wird die folgende mathematische Beziehung hergestellt:
ΦUND = c ∙ Q.enc
Wo c ist die Proportionalitätskonstante.
Erklärung des Gaußschen Gesetzes
Um die Bedeutung des Gaußschen Gesetzes zu verstehen, müssen die in seiner Aussage enthaltenen Konzepte erläutert werden: elektrische Ladung, elektrisches Feld und elektrisches Feld fließen durch eine Oberfläche..
Elektrische Ladung
Elektrische Ladung ist eine der grundlegenden Eigenschaften der Materie. Ein geladenes Objekt kann eine von zwei Arten von Ladungen haben: positive oder negative, obwohl die Objekte normalerweise neutral sind, dh sie haben die gleiche negative Ladungsmenge wie positive..
Zwei geladene Objekte des gleichen Typs stoßen sich gegenseitig ab, auch wenn kein Kontakt zwischen ihnen besteht und sie sich in einem Vakuum befinden. Im Gegenteil, wenn jeder der Körper Ladungen eines anderen Zeichens hat, dann ziehen sie sich gegenseitig an. Diese Art der Wechselwirkung in der Ferne wird als elektrische Wechselwirkung bezeichnet..
Im internationalen System der SI-Einheiten wird die elektrische Ladung in gemessen Coulomb (C). Der negative elementare Ladungsträger ist der Elektron mit Last von -1,6 x 10-19C. und der positive elementare Ladungsträger ist das Proton mit einem Ladungswert +1,6 x 10-19C.. Typischerweise haben geladene Körper zwischen 10-9C. Y. 10-3C..
elektrisches Feld
Ein elektrisch geladener Körper verändert den Raum in seiner Umgebung und füllt ihn mit etwas Unsichtbarem, das als elektrisches Feld bezeichnet wird. Um zu wissen, dass dieses Feld vorhanden ist, ist eine positive Testpunktladung erforderlich.
Wenn die Testladung an einem Ort platziert wird, an dem ein elektrisches Feld vorhanden ist, tritt eine Kraft in einer bestimmten Richtung auf sie auf, die der des elektrischen Feldes entspricht. Die Feldstärke ist die Kraft auf die Testladung geteilt durch die Ladungsmenge auf die Testladung. Dann die Einheiten des elektrischen Feldes UND im internationalen Einheitensystem sind Newton Komm herein Coulomb:: [E] = N / C..
Positive Punktladungen erzeugen ein nach außen gerichtetes radiales Feld, während negative Ladungen ein radial nach innen gerichtetes Feld erzeugen. Weiterhin fällt das durch eine Punktladung erzeugte Feld mit der Umkehrung des Quadrats der Entfernung zu dieser Ladung ab.
Elektrische Feldlinien
Michael Faraday (1791 - 1867) war der erste, der ein mentales Bild des elektrischen Feldes hatte und es sich als Linien vorstellte, die der Richtung des Feldes folgen. Bei einer positiven Punktladung sind diese Linien von der Mitte nach außen radial. Wo die Linien näher beieinander liegen, ist das Feld intensiver und weniger intensiv, wo sie weiter voneinander entfernt sind.
Positive Ladungen sind die Quellen, aus denen die elektrischen Feldlinien austreten, während negative Ladungen die Senken der Linien sind..
Elektrische Feldlinien schließen sich nicht an sich selbst an. In einer Reihe von Ladungen verlassen die Linien die positiven Ladungen und treten in die positiven ein, aber sie können auch die Unendlichkeit erreichen oder von dort kommen.
Sie schneiden sich auch nicht und an jedem Punkt im Raum ist der elektrische Feldvektor tangential zur Feldlinie und proportional zur Dichte der Linien dort..

Elektrischer Feldfluss
Elektrische Feldlinien ähneln den Stromlinien eines sanft fließenden Flusses, daher wurde das Konzept des elektrischen Feldflusses geboren..
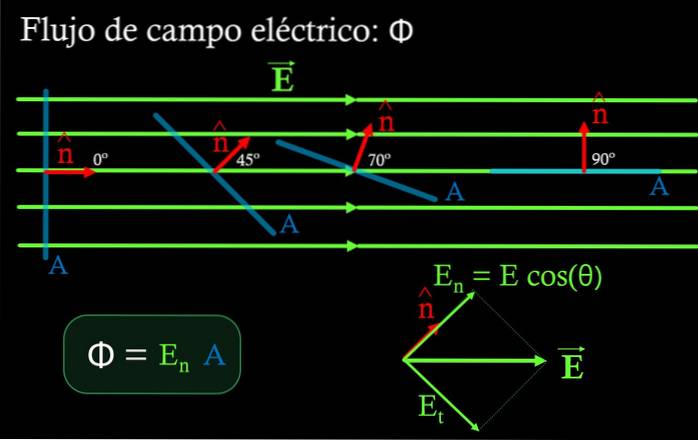
In einem Bereich, in dem das elektrische Feld gleichmäßig ist, ist der Fluss Φ durch eine flache Oberfläche das Produkt der Normalkomponente des Feldes E.n zu dieser Oberfläche, multipliziert mit der Fläche ZU Von dem selben:
Φ = E.n ∙ A.
Komponente E.n wird erhalten, indem die Größe des elektrischen Feldes mit dem Kosinus des Winkels multipliziert wird, der zwischen dem Feld und dem Einheitsnormalenvektor zur Oberfläche gebildet wird ZU. (siehe Abbildung 4).
Gaußsche Gesetzesanwendungen
Das Gaußsche Gesetz kann angewendet werden, um das elektrische Feld zu bestimmen, das durch Ladungsverteilungen mit einem hohen Grad an Symmetrie erzeugt wird.
Elektrisches Feld einer Punktladung
Eine Punktladung erzeugt ein radiales elektrisches Feld, das ausgeht, wenn die Ladung positiv ist, und andernfalls eingeht..
Wenn man als Gaußsche Oberfläche eine imaginäre Kugel mit dem Radius R und konzentrisch zur Ladung Q wählt, ist das elektrische Feld an allen Punkten auf der Oberfläche dieser Kugel gleich groß und seine Richtung ist immer normal zur Oberfläche. In diesem Fall ist der elektrische Feldfluss also das Produkt aus der Größe des Feldes und der Gesamtfläche der sphärischen Oberfläche:
Φ = E ∙ A = E ∙ 4πRzwei
Andererseits besagt das Gaußsche Gesetz, dass: Φ = c, Q die Proportionalitätskonstante ist c. Bei der Arbeit in Einheiten des internationalen Messsystems ist die Konstante c ist die Umkehrung der Permittivität des Vakuums, und das Gaußsche Gesetz ist wie folgt formuliert:
Φ = (1 / εoder) ∙ Q.
Unter Berücksichtigung des Ergebnisses, das für den Fluss nach dem Gaußschen Gesetz erhalten wurde, haben wir:
E ∙ 4πRzwei = (1 / εoder) ∙ Q.
Und für die Größenordnung von UND Ergebnis:
E = (1 / 4πεoder) ∙ (Q / R.zwei)
Was voll und ganz mit Coulombs Gesetz des elektrischen Feldes einer Punktladung übereinstimmt.
Ausbildung
Übung 1
Zwei Punktladungen liegen willkürlich innerhalb einer Gaußschen Oberfläche S. Einer von ihnen hat bekanntlich einen Wert von +3 nC (3 Nano-Coulomb). Wenn der elektrische Nettofeldfluss durch die Gaußsche Oberfläche 113 (N / C) m beträgtzwei, Was ist der Wert der anderen Last?
Lösung
Das Gaußsche Gesetz besagt das
ΦUND = (1 / εoder) ∙ Q.enc
Daher beträgt die eingeschlossene Nettoladung:
Q.enc = ΦUND ∙ εoder
Ersetzen der Datenergebnisse:
Q.enc = 113 (N / C) mzwei 85 8,85 x 10-12 (C.zwei m-zwei N.-1) = 1 x 10-9 C = 1 nC.
Aber Q.enc = + Q - q, Wenn die positive Ladung einen bekannten Wert von +3 nC hat, beträgt die Ladung daher notwendigerweise -2 nC.
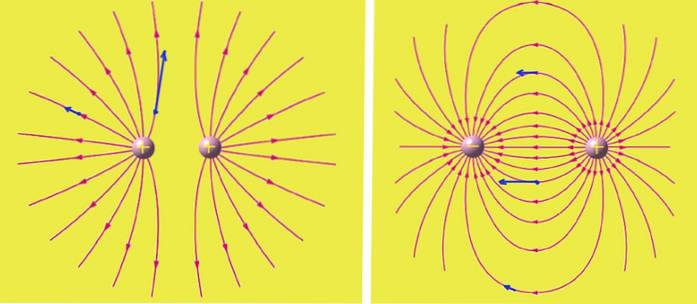
Übung 2
In Abbildung 2 gibt es eine Anordnung (links) von zwei positiven Ladungen mit jeweils einem Wert + q und eine andere Anordnung (rechts) mit einer Ladung + q und der anderen -q. Jede Anordnung ist in einer imaginären Box mit all ihren 10 cm Kanten eingeschlossen. Wenn | q | = 3 μC, ermitteln Sie für jede Anordnung den elektrischen Nettofeldfluss durch die Box.
Lösung
In der ersten Anordnung beträgt der Nettofluss:
ΦUND = (1 / εoder) ∙ (+ q + q) = 678000 (N / C) mzwei
In der Anordnung auf der rechten Seite ist der Nettofluss durch die imaginäre Box, die das Ladungspaar enthält, Null..
Verweise
- Cosenza, M. Elektromagnetismus. Universität der Anden.
- Díaz, R. Elektrodynamik: Notizen. Nationale Universität von Kolumbien.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 6. Elektromagnetismus. Herausgegeben von Douglas Figueroa (USB).
- Jackson, J. D. Klassische Elektrodynamik. 3 .. Ed. Wiley.
- Tarazona, C. Einführung in die Elektrodynamik. Editorial Manuela Beltrán Universität.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.