Demonstration pythagoreischer Identitäten, Beispielübungen

Sie sind Pythagoreische Identitäten Alle trigonometrischen Gleichungen, die für jeden Wert des Winkels gelten und auf dem Satz von Pythagoras basieren. Die bekannteste der pythagoreischen Identitäten ist die grundlegende trigonometrische Identität:

Sen.^zwei(α) + Cos^zwei(α) = 1

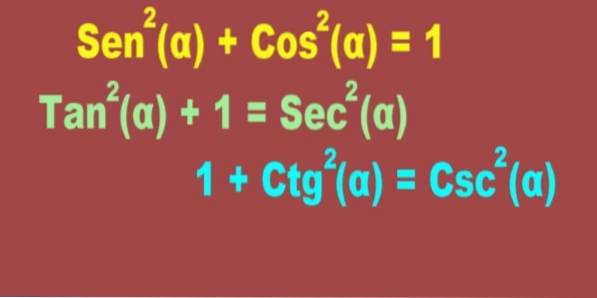
Als nächstes in der Wichtigkeit und ich benutze die pythagoreische Identität der Tangente und der Sekante:

So^zwei(α) + 1 = Sek^zwei(α)

Und die pythagoreische trigonometrische Identität, an der der Kotangens und der Kosekant beteiligt sind:

1 + Ctg^zwei(α) = Csc^zwei(α)

Artikelverzeichnis

• 1 Demo
  • 1.1 Sinus und Cosinus
  • 1.2 Die grundlegende Identität
  • 1.3 Die Tangentenachse
  • 1.4 Die pythagoreische Identität der Tangente
• 2 Beispiel
• 3 Gelöste Übungen
  • 3.1 Übung 1
  • 3.2 Übung 2
• 4 Referenzen

Demonstration

Die trigonometrischen Verhältnisse Brust Y. Kosinus Sie werden in einem Kreis mit dem Radius eins (1) dargestellt, der als trigonometrischer Kreis bekannt ist. Der Kreis hat einen Mittelpunkt am Ursprung der Koordinaten O..

Die Winkel werden von der positiven Halbachse des X aus gemessen, beispielsweise vom Winkel α in Abbildung 2 (siehe unten). Gegen den Uhrzeigersinn, wenn der Winkel positiv ist, und im Uhrzeigersinn, wenn es sich um einen negativen Winkel handelt.

Der Strahl mit Ursprung O und Winkel α wird gezeichnet, der den Einheitskreis am Punkt P abfängt. Punkt P wird orthogonal auf die horizontale Achse X projiziert, wodurch Punkt C entsteht. In ähnlicher Weise wird P senkrecht auf die vertikale Achse Y projiziert, wodurch Platz für Punkt entsteht S..

Wir haben das rechtwinklige OCP bei C.. 

Sinus und Cosinus

Es sei daran erinnert, dass das trigonometrische Verhältnis Brust wird in einem rechtwinkligen Dreieck wie folgt definiert:

Der Sinus eines Winkels des Dreiecks ist das Verhältnis oder der Quotient zwischen dem dem Winkel gegenüberliegenden Bein und der Hypotenuse des Dreiecks.

Auf das Dreieck OCP von Abbildung 2 angewendet würde es folgendermaßen aussehen:

Sen (α) = CP / OP

aber CP = OS und OP = 1, so dass:

Sen (α) = OS

Dies bedeutet, dass das Projektions-OS auf der Y-Achse einen Wert hat, der dem Sinus des angezeigten Winkels entspricht. Es ist zu beachten, dass der Maximalwert des Sinus eines Winkels (+1) bei α = 90º und der Minimalwert (-1) bei α = -90º oder α = 270º auftritt.

In ähnlicher Weise ist der Kosinus eines Winkels der Quotient zwischen dem dem Winkel benachbarten Bein und der Hypotenuse des Dreiecks..

Auf das Dreieck OCP von Abbildung 2 angewendet würde es folgendermaßen aussehen:

Cos (α) = OC / OP

aber OP = 1, so dass:

Cos (α) = OC

Dies bedeutet, dass die Projektion OC auf der X-Achse einen Wert hat, der dem Sinus des gezeigten Winkels entspricht. Es ist zu beachten, dass der Maximalwert des Cosinus (+1) auftritt, wenn α = 0º oder α = 360º ist, während der Minimalwert des Cosinus (-1) ist, wenn α = 180º ist.

Die grundlegende Identität

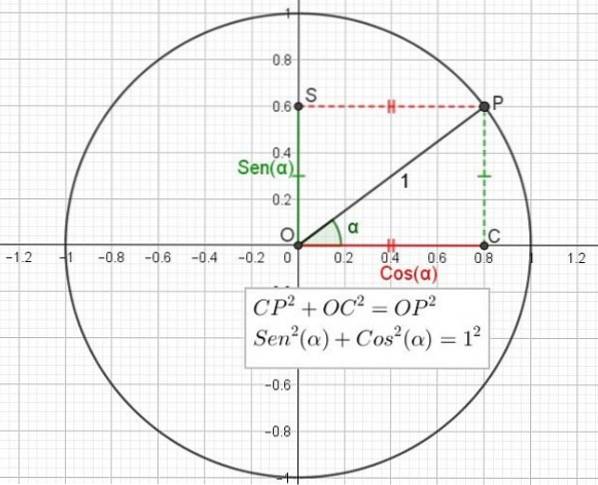
Für das rechtwinklige Dreieck OCP in C wird der Satz von Pythagoras angewendet, der besagt, dass die Summe des Quadrats der Beine gleich dem Quadrat der Hypotenuse ist:

CP^zwei + OK^zwei = OP^zwei

Es wurde jedoch bereits gesagt, dass CP = OS = Sen (α), OC = Cos (α) und OP = 1, so dass der vorherige Ausdruck als Funktion des Sinus und Cosinus des Winkels umgeschrieben werden kann:

Sen.^zwei(α) + Cos^zwei(α) = 1

Die Achse der Tangente

So wie die X-Achse im trigonometrischen Kreis die Kosinusachse und die Y-Achse die Sinusachse ist, gibt es auch die Tangentenachse (siehe Abbildung 3), die genau die Tangentenlinie zum Einheitskreis am Punkt B von ist Koordinaten (1, 0). 

Wenn Sie den Wert der Tangente eines Winkels wissen möchten, zeichnen Sie den Winkel von der positiven Halbachse des X, der Schnittpunkt des Winkels mit der Achse der Tangente definiert einen Punkt Q, die Länge des Segments OQ ist die Tangente des Winkels.

Dies liegt daran, dass per Definition die Tangente des Winkels α das gegenüberliegende Bein QB zwischen dem benachbarten Bein OB ist. Das heißt, Tan (α) = QB / OB = QB / 1 = QB.

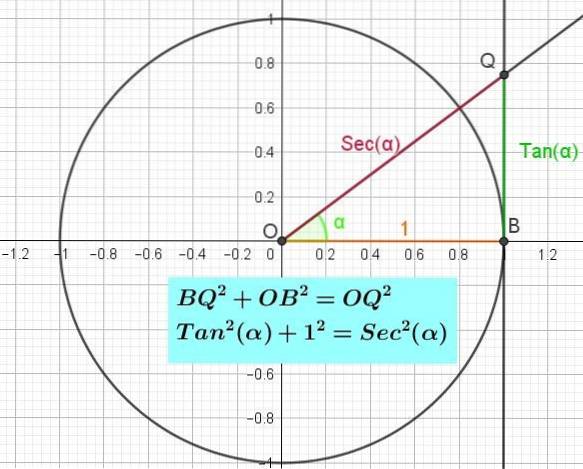
Die pythagoreische Identität der Tangente

Die pythagoreische Identität der Tangente kann unter Berücksichtigung des OBQ des rechtwinkligen Dreiecks bei B nachgewiesen werden (Abbildung 3). Wenn wir den Satz von Pythagoras auf dieses Dreieck anwenden, haben wir diesen BQ^zwei + OB^zwei = OQ^zwei. Es wurde jedoch bereits gesagt, dass BQ = Tan (α), OB = 1 und OQ = Sec (α), so dass wir in der pythagoreischen Gleichheit das rechtwinklige Dreieck OBQ ersetzen:

So^zwei(α) + 1 = Sek^zwei(α).

Beispiel

Überprüfen Sie, ob die pythagoreischen Identitäten im rechtwinkligen Dreieck mit den Beinen AB = 4 und BC = 3 erfüllt sind.

Lösung: Die Beine sind bekannt, die Hypotenuse muss bestimmt werden, das heißt:

AC = √ (AB ^ 2 + BC ^ 2) = √ (4 ^ 2 + 3 ^ 2) = √ (16 + 9) = √ (25) = 5.

Der Winkel ∡BAC heißt α, ∡BAC = α. Nun werden die trigonometrischen Verhältnisse bestimmt:

Sen α = BC / AC = 3/5 

Cos α = AB / AC = 4/5 

Also ist α = BC / AB = 3/4 

Cotan α = AB / BC = 4/3 

Sec α = AC / AB = 5/4 

Csc α = AC / BC = 5/3

Es beginnt mit der grundlegenden trigonometrischen Identität:

Sen.^zwei(α) + Cos^zwei(α) = 1

(3/5) ^ 2 + (4/5) ^ 2 = 9/25 + 16/25 = (9 + 16) / 25 = 25/25 = 1

Es wird der Schluss gezogen, dass es erfüllt ist.

- Die nächste pythagoreische Identität ist die der Tangente:

So^zwei(α) + 1 = Sek^zwei(α)

(3/4) ^ 2 + 1 = 9/16 + 16/16 = (9 + 16) / 16 = 25/16 = (5/4) ^ 2

Und es wird der Schluss gezogen, dass die Identität der Tangente überprüft wird.

- Ähnlich wie beim Kotangens:

1 + Ctg^zwei(α) = Csc^zwei(α)

1+ (4/3) ^ 2 = 1 + 16/9 = 25/9 = (5/3) ^ 2

Es wird der Schluss gezogen, dass es auch erfüllt ist, womit die Aufgabe der Überprüfung der pythagoreischen Identitäten für das gegebene Dreieck abgeschlossen ist.

Gelöste Übungen

Beweisen Sie die folgenden Identitäten basierend auf den Definitionen der trigonometrischen Verhältnisse und der pythagoreischen Identitäten.

Übung 1

Beweisen Sie, dass Cos^zwei x = (1 + Sen x) (1 - Sen x).

Lösung: Auf der rechten Seite wird das bemerkenswerte Produkt der Multiplikation eines Binomials mit seinem Konjugat erkannt, das bekanntlich ein Unterschied von Quadraten ist:

Cos^zwei x = 1^zwei - Sen.^zwei x

Dann geht der Begriff mit Sinus auf der rechten Seite mit geändertem Vorzeichen auf die linke Seite über:

Cos^zwei x + Sen.^zwei x = 1

Unter Hinweis darauf, dass die grundlegende trigonometrische Identität erreicht wurde, wird der Schluss gezogen, dass der gegebene Ausdruck eine Identität ist, das heißt, er gilt für jeden Wert von x.

Übung 2

Zeigen Sie ausgehend von der grundlegenden trigonometrischen Identität und unter Verwendung der Definitionen der trigonometrischen Verhältnisse die pythagoreische Identität des Kosekanten.

Lösung: Die grundlegende Identität ist:

Sen.^zwei(x) + Cos^zwei(x) = 1

Beide Mitglieder sind zwischen Sen aufgeteilt^zwei(x) und der Nenner wird im ersten Mitglied verteilt:

Sen.^zwei(x) / Sen.^zwei(x) + Cos^zwei(x) / Sen.^zwei(x) = 1 / Sen.^zwei(x)

Es ist vereinfacht:

1 + (Cos (x) / Sen (x)) ^ 2 = (1 / Sen (x)) ^ 2

Cos (x) / Sen (x) = Cotan (x) ist eine (nicht pythagoreische) Identität, die durch die Definition der trigonometrischen Verhältnisse verifiziert wird. Das gleiche passiert mit der folgenden Identität: 1 / Sen (x) = Csc (x).

Schließlich müssen Sie:

1 + Ctg^zwei(x) = Csc^zwei(x)

Verweise

1. Baldor J. (1973). Ebenen- und Raumgeometrie mit einer Einführung in die Trigonometrie. Zentralamerikanisches Kultur. AC.
2. C. E. A. (2003). Elemente der Geometrie: mit Übungen und Geometrie des Kompasses. Universität von Medellin.
3. Campos, F., Cerecedo, F. J. (2014). Mathematik 2. Grupo Editorial Patria.
4. IGER. (s.f.). Mathematik Erstes Semester Tacaná. IGER.
5. Jr. Geometrie. (2014). Polygone. Lulu Press, Inc..
6. Miller, Heeren & Hornsby. (2006). Mathematik: Argumentation und Anwendungen (Zehnte Ausgabe). Pearson Ausbildung.
7. Patiño, M. (2006). Mathematik 5. Editorial Progreso.
8. Wikipedia. Trigonometrie-Identitäten und -Formeln. Wiederhergestellt von: es.wikipedia.com