
Homothekeneigenschaften, -typen und -beispiele
Das Homothek Es ist eine geometrische Änderung in der Ebene, bei der ausgehend von einem festen Punkt, der als Mittelpunkt (O) bezeichnet wird, die Abstände mit einem gemeinsamen Faktor multipliziert werden. Auf diese Weise entspricht jeder Punkt P einem anderen Punkt P'-Produkt der Transformation, und diese sind mit Punkt O ausgerichtet.
In der Homothez geht es dann um eine Entsprechung zwischen zwei geometrischen Figuren, wobei die transformierten Punkte als homothetisch bezeichnet werden und diese mit einem festen Punkt und mit Segmenten parallel zueinander ausgerichtet sind..

Artikelverzeichnis
- 1 Homothek
- 2 Eigenschaften
- 3 Typen
- 3.1 Direkte Homothek
- 3.2 Umgekehrte Homothek
- 4 Zusammensetzung
- 5 Beispiele
- 5.1 Erstes Beispiel
- 5.2 Zweites Beispiel
- 6 Referenzen
Homotheke
Homothecy ist eine Transformation, die kein kongruentes Bild hat, weil aus einer Figur eine oder mehrere Figuren von größerer oder kleinerer Größe als die ursprüngliche Figur erhalten werden; Das heißt, die Homothez verwandelt ein Polygon in ein anderes ähnliches.
Damit die Homothez erfüllt werden kann, müssen Punkt zu Punkt und Linie zu Linie übereinstimmen, damit die Paare homologer Punkte mit einem dritten Fixpunkt ausgerichtet sind, der das Zentrum der Homothetik darstellt.
Ebenso müssen die Linienpaare, die sie verbinden, parallel sein. Die Beziehung zwischen solchen Segmenten ist eine Konstante, die als Homothecy Ratio (k) bezeichnet wird; so, dass Homothez definiert werden kann als:
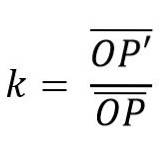
Um diese Art der Transformation durchzuführen, wählen wir zunächst einen beliebigen Punkt, der das Zentrum der Homotheke sein wird.
Ab diesem Punkt werden Liniensegmente für jeden Scheitelpunkt der zu transformierenden Figur gezeichnet. Der Maßstab, in dem die Reproduktion der neuen Figur erfolgt, ergibt sich aus dem Verhältnis der Homothez (k).
Eigenschaften
Eine der Haupteigenschaften der Homothez ist, dass aus homothetischen Gründen (k) alle homothetischen Figuren ähnlich sind. Andere bemerkenswerte Eigenschaften umfassen die folgenden:
- Das Zentrum der Homothecia (O) ist der einzige Doppelpunkt und wird selbst; das heißt, es variiert nicht.
- Die Linien, die durch das Zentrum verlaufen, werden in sich selbst umgewandelt (sie sind doppelt), aber die Punkte, aus denen es besteht, sind nicht doppelt.
- Die Linien, die nicht durch die Mitte verlaufen, werden zu parallelen Linien. auf diese Weise bleiben die Homothekiewinkel gleich.
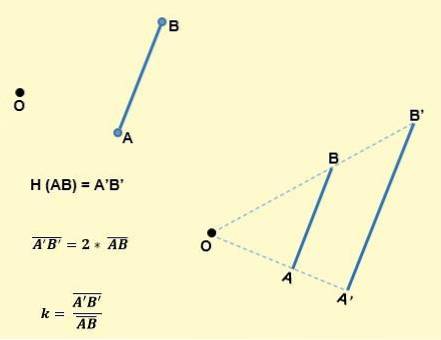
- Das Bild eines Segments durch eine Homothez von Zentrum O und Verhältnis k ist ein dazu paralleles Segment und hat das k-fache seiner Länge. Wie in der folgenden Abbildung zu sehen ist, führt beispielsweise ein Segment AB nach Homothek zu einem anderen Segment A'B ', so dass AB parallel zu A'B' ist und k:
- Homothetische Winkel sind kongruent; das heißt, sie haben das gleiche Maß. Daher ist das Bild eines Winkels ein Winkel mit der gleichen Amplitude.
Andererseits variiert die Homothez in Abhängigkeit vom Wert ihres Verhältnisses (k), und die folgenden Fälle können auftreten:
- Wenn die Konstante k = 1 ist, sind alle Punkte fest, weil sie sich selbst transformieren. Somit stimmt die homothetische Figur mit der ursprünglichen überein und die Transformation wird als Identitätsfunktion bezeichnet.
- Wenn k ≠ 1 ist, ist der einzige feste Punkt das Zentrum der Homothese (O)..
- Wenn k = -1 ist, wird die Homothez zu einer zentralen Symmetrie (C); Das heißt, eine Drehung um C in einem Winkel von 180 ° erfolgtoder.
- Wenn k> 1 ist, ist die Größe der transformierten Figur größer als die Größe des Originals.
- Ja 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.
- Ja -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.
- Wenn k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.
Typen
Die Homothek kann je nach Wert ihres Verhältnisses (k) auch in zwei Typen eingeteilt werden:
Direkte Homothek
Es tritt auf, wenn die Konstante k> 0 ist; Das heißt, die homothetischen Punkte befinden sich in Bezug auf das Zentrum auf derselben Seite:
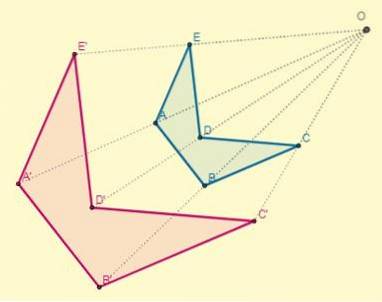
Der Proportionalitätsfaktor oder das Ähnlichkeitsverhältnis zwischen den direkten homothetischen Zahlen ist immer positiv.
Reverse Homothecy
Es tritt auf, wenn die Konstante k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:
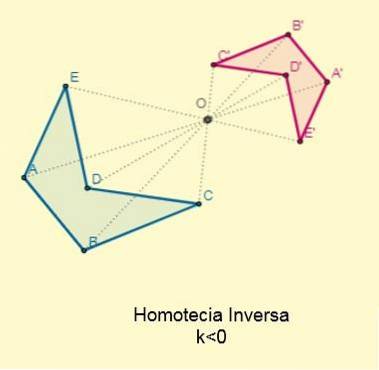
Der Proportionalitätsfaktor oder das Ähnlichkeitsverhältnis zwischen den inversen homothetischen Zahlen ist immer negativ.
Komposition
Wenn mehrere Bewegungen nacheinander ausgeführt werden, bis eine Figur erhalten wird, die dem Original entspricht, tritt eine Zusammensetzung von Bewegungen auf. Die Zusammensetzung mehrerer Sätze ist ebenfalls eine Bewegung.
Die Zusammensetzung zwischen zwei Homotheken führt zu einer neuen Homotheke; das heißt, es gibt ein Produkt von Homothetien, bei denen das Zentrum mit dem Zentrum der beiden ursprünglichen Transformationen ausgerichtet wird und das Verhältnis (k) das Produkt der beiden Verhältnisse ist.
So ist in der Zusammensetzung zweier Homotheken H.1(ODER1, k1) und H.zwei(ODERzwei, kzwei), die Multiplikation ihrer Verhältnisse: k1 x kzwei = 1 führt zu einer Homothez des Verhältnisses k3 = K.1 x kzwei. Das Zentrum dieser neuen Homotheke (O.3) befindet sich in der Zeile O.1 ODERzwei.
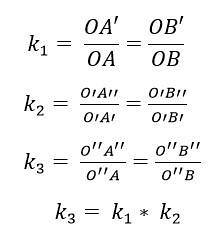
Homothecia entspricht einer flachen und irreversiblen Veränderung; Wenn zwei Homothetien angewendet werden, die das gleiche Zentrum und Verhältnis haben, aber ein anderes Vorzeichen haben, wird die ursprüngliche Figur erhalten.
Beispiele
Erstes Beispiel
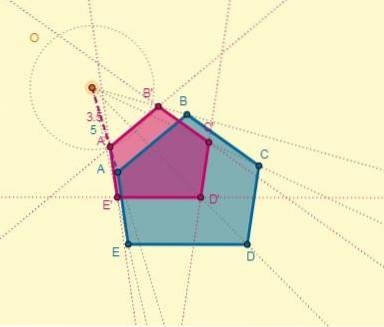
Wenden Sie eine Homothek auf das angegebene Polygon mit dem Zentrum (O) an, das 5 cm vom Punkt A entfernt liegt und dessen Verhältnis k = 0,7 beträgt.
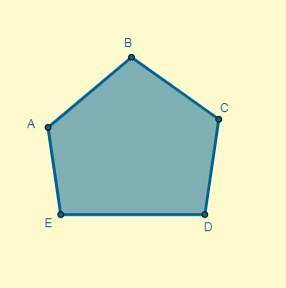
Lösung
Jeder Punkt wird als Zentrum der Homothek gewählt, und von diesem Punkt aus werden Strahlen durch die Eckpunkte der Figur gezogen:
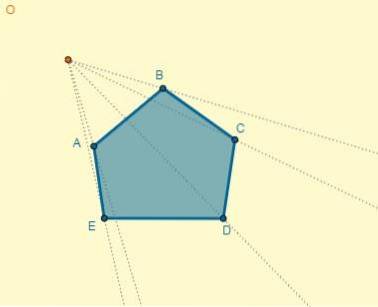
Wir haben, dass der Abstand vom Zentrum (O) zum Punkt A OA = 5 ist; Damit kann der Abstand eines der homothetischen Punkte (OA ') bestimmt werden, auch in dem Wissen, dass k = 0,7:
OA '= k x OA.
OA '= 0,7 × 5 = 3,5.
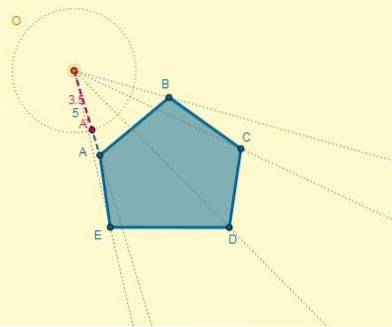
Der Prozess kann für jeden Scheitelpunkt durchgeführt werden, oder das homothetische Polygon kann auch gezeichnet werden, wobei zu berücksichtigen ist, dass die beiden Polygone parallele Seiten haben:
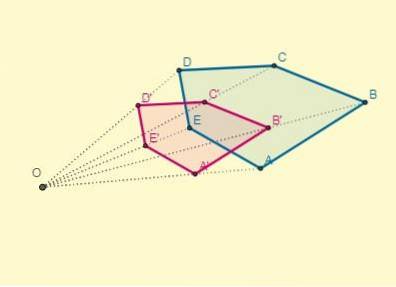
Schließlich sieht die Transformation folgendermaßen aus:
Zweites Beispiel
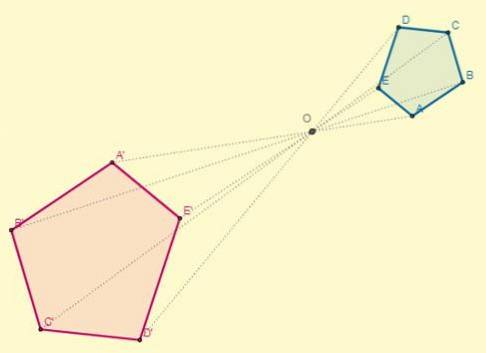
Wenden Sie eine Homothek auf das angegebene Polygon mit dem Zentrum (O) an, das 8,5 cm vom Punkt C entfernt liegt und dessen y-Verhältnis k = -2 ist.
Lösung
Der Abstand vom Zentrum (O) zum Punkt C beträgt OC = 8,5; Mit diesen Daten ist es möglich, den Abstand eines der homothetischen Punkte (OC ') zu bestimmen, auch wenn man weiß, dass k = -2:
OC '= k x OC.
OC '= -2 x 8,5 = -17
Nach dem Zeichnen der Segmente der Eckpunkte des transformierten Polygons befinden sich die Anfangspunkte und ihre Homothetik an den entgegengesetzten Enden in Bezug auf die Mitte:
Verweise
- Álvaro Rendón, A. R. (2004). Technische Zeichnung: Aufgabenheft.
- Antonio Álvarez de la Rosa, J.L. (2002). Affinität, Homologie und Homothez.
- Baer, R. (2012). Lineare Algebra und projektive Geometrie. Courier Corporation.
- Hebert, Y. (1980). Allgemeine Mathematik, Wahrscheinlichkeiten und Statistik.
- Meserve, B. E. (2014). Grundlegende Konzepte der Geometrie. Courier Corporation.
- Nachbin, L. (1980). Einführung in die Algebra. Reverte.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.