
Millikan Experimentierverfahren, Erklärung, Bedeutung
Das Millikan-Experiment, Die von Robert Millikan (1868-1953) zusammen mit seinem Schüler Harvey Fletcher (1884-1981) durchgeführte Studie begann 1906 mit dem Ziel, die Eigenschaften elektrischer Ladung zu untersuchen und die Bewegung von Tausenden von Öltropfen in der Mitte einer Uniform zu analysieren elektrisches Feld.
Die Schlussfolgerung war, dass die elektrische Ladung keinen willkürlichen Wert hatte, sondern ein Vielfaches von 1,6 x 10-19 C, das ist die Grundladung des Elektrons. Zusätzlich wurde die Masse des Elektrons gefunden.
Zuvor war der Physiker J.J. Thompson hatte experimentell die Ladung-Masse-Beziehung dieses Elementarteilchens gefunden, das er "Korpuskel" nannte, aber nicht die Werte jeder Größe separat..
Aus dieser Ladung-Masse-Beziehung und der Ladung des Elektrons wurde der Wert seiner Masse bestimmt: 9,11 x 10-31 Kg.
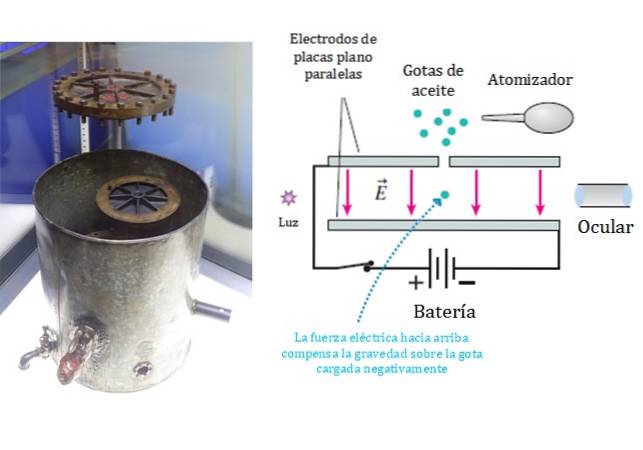
Um ihren Zweck zu erreichen, verwendeten Millikan und Fletcher einen Zerstäuber, mit dem ein feiner Nebel aus Öltröpfchen besprüht wurde. Einige der Tröpfchen wurden aufgrund von Reibung in der Düse elektrisch geladen.
Die geladenen Tropfen setzten sich langsam auf parallelen ebenen Plattenelektroden ab, wo einige durch ein kleines Loch in der oberen Platte gingen, wie in der Abbildung in Abbildung 1 gezeigt.
Innerhalb der parallelen Platten ist es möglich, ein gleichmäßiges elektrisches Feld senkrecht zu den Platten zu erzeugen, deren Größe und Polarität durch Modifizieren der Spannung gesteuert wurden..
Das Verhalten der Tropfen wurde beobachtet, indem das Innere der Platten mit hellem Licht beleuchtet wurde..
Artikelverzeichnis
- 1 Erklärung des Experiments
- 1.1 Die Masse des Öltropfens
- 2 Bedeutung
- 2.1 Tropfen mit verschiedenen Ladungen
- 3 Beispiel
- 3.1 Einen Tropfen Öl schweben lassen
- 4 Referenzen
Erklärung des Experiments
Wenn der Tropfen eine Ladung hat, übt das zwischen den Platten erzeugte Feld eine Kraft auf ihn aus, die der Schwerkraft entgegenwirkt..
Und wenn es auch gelingt, aufgehängt zu bleiben, bedeutet dies, dass das Feld eine vertikale Kraft nach oben ausübt, die die Schwerkraft genau ausgleicht. Diese Bedingung hängt vom Wert von ab Was, die Last des Tropfens.
In der Tat beobachtete Millikan, dass nach dem Einschalten des Feldes einige Tropfen aufgehängt wurden, andere anfingen zu steigen oder weiter abzusteigen.
Durch Einstellen des Wertes des elektrischen Feldes - beispielsweise mittels eines variablen Widerstands - könnte ein Tropfen dazu gebracht werden, in den Platten schwebend zu bleiben. Obwohl es in der Praxis nicht einfach ist, dies zu erreichen, wirkt nur die vom Feld und der Schwerkraft ausgeübte Kraft auf den Tropfen..
Wenn die Masse des Tropfens ist m und seine Last ist Was, zu wissen, dass die Kraft proportional zum angelegten Größenfeld ist UND, Newtons zweites Gesetz besagt, dass beide Kräfte ausgeglichen sein müssen:
mg = q.E.
q = mg / E.
Der Wert von G, Die Beschleunigung der Schwerkraft ist ebenso bekannt wie die Größe UND des Feldes, das von der Spannung abhängt V. zwischen den Platten und dem Spalt zwischen ihnen hergestellt L., Was:
E = V / L.
Die Frage war, die Masse des winzigen Öltropfens zu finden. Sobald dies erreicht ist, bestimmen Sie die Last Was es ist durchaus möglich. Natürlich das m Y. Was sind jeweils die Masse und Ladung des Öltropfens, nicht das Elektron.
Aber ... der Tropfen wird geladen, weil er Elektronen verliert oder gewinnt, so dass sein Wert mit der Ladung des Teilchens zusammenhängt.
Die Masse des Öltropfens
Das Problem von Millikan und Fletcher bestand darin, die Masse eines Tropfens zu bestimmen, was aufgrund seiner geringen Größe keine leichte Aufgabe war..
Wenn Sie die Dichte des Öls kennen und das Volumen des Tropfens haben, kann die Masse gelöst werden. Das Volumen war aber auch sehr klein, so dass herkömmliche Methoden nicht hilfreich waren..
Die Forscher wussten jedoch, dass solche kleinen Objekte nicht frei fallen, da der Widerstand der Luft oder der Umwelt durch Verlangsamung ihrer Bewegung eingreift. Obwohl das Teilchen, wenn es bei ausgeschaltetem Feld freigesetzt wird, eine beschleunigte vertikale Bewegung nach unten erfährt, fällt es mit konstanter Geschwindigkeit ab..
Diese Geschwindigkeit wird als "Endgeschwindigkeit" oder "Grenzgeschwindigkeit" bezeichnet, was im Fall einer Kugel von ihrem Radius und der Viskosität der Luft abhängt..
In Abwesenheit eines Feldes maßen Millikan und Fletcher die Zeit, die die Tropfen brauchten, um zu fallen. Unter der Annahme, dass die Tropfen kugelförmig waren und den Wert der Viskosität der Luft hatten, gelang es ihnen, den Radius indirekt aus der Endgeschwindigkeit zu bestimmen.
Diese Geschwindigkeit wird durch Anwendung des Stokes'schen Gesetzes ermittelt und hier ist seine Gleichung:

-vt ist die Endgeschwindigkeit
-R. ist der Radius des Tropfens (sphärisch)
-η ist die Viskosität von Luft
-ρ ist die Dichte des Tropfens
Bedeutung
Millikans Experiment war entscheidend, da es mehrere Schlüsselaspekte in der Physik enthüllte:
I) Die Elementarladung ist die des Elektrons, dessen Wert 1,6 x 10 beträgt -19 C, eine der grundlegenden Konstanten der Wissenschaft.
II) Jede andere elektrische Ladung kommt in Vielfachen der Grundladung.
III) Kenntnis der Ladung des Elektrons und der Ladungs-Massen-Beziehung von J.J. Thomson war es möglich, die Masse des Elektrons zu bestimmen.
III) Bei Partikeln, die so klein wie Elementarteilchen sind, sind die Gravitationseffekte im Vergleich zur Elektrostatik vernachlässigbar.

Für diese Entdeckungen erhielt Millikan 1923 den Nobelpreis für Physik. Sein Experiment ist auch deshalb relevant, weil er diese grundlegenden Eigenschaften der elektrischen Ladung ausgehend von einer einfachen Instrumentierung und der Anwendung von Gesetzen, die allen bekannt sind, bestimmt hat..
Millikan wurde jedoch dafür kritisiert, dass er viele Beobachtungen in seinem Experiment ohne ersichtlichen Grund verworfen hatte, um den statistischen Fehler der Ergebnisse zu verringern und sie "präsentabler" zu machen..
Tropfen mit verschiedenen Gebühren
Millikan hat in seinem Experiment viele, viele Tropfen gemessen und nicht alle waren Öl. Er versuchte auch Quecksilber und Glycerin. Wie bereits erwähnt, begann das Experiment 1906 und dauerte einige Jahre. Drei Jahre später, 1909, wurden die ersten Ergebnisse veröffentlicht.
Während dieser Zeit erhielt er eine Vielzahl geladener Tropfen, indem er Röntgenstrahlen durch die Platten schlug, um die Luft zwischen ihnen zu ionisieren. Auf diese Weise werden geladene Teilchen freigesetzt, die die Tropfen aufnehmen können.
Darüber hinaus konzentrierte er sich nicht nur auf die suspendierten Tröpfchen. Millikan beobachtete, dass beim Anstieg der Tropfen auch die Anstiegsrate je nach zugeführter Last variierte..
Und wenn der Tropfen abfiel, änderte diese zusätzliche Ladung, die dank des Eingriffs der Röntgenstrahlen hinzugefügt wurde, die Geschwindigkeit nicht, da jede Masse von Elektronen, die dem Tropfen hinzugefügt wurde, im Vergleich zur Masse des Tropfens selbst winzig ist..
Unabhängig davon, wie viel Ladung er hinzufügte, stellte Millikan fest, dass alle Tropfen Ladungen mit ganzzahligen Vielfachen eines bestimmten Wertes erhielten und, die Grundeinheit, die, wie gesagt, die Ladung des Elektrons ist.
Millikan erzielte zunächst 1.592 x 10-19 C für diesen Wert etwas weniger als derzeit angenommen, dh 1.602 x 10-19 Das Verhältnis kann der Wert gewesen sein, den Sie der Viskosität der Luft in der Gleichung gegeben haben, um die Endgeschwindigkeit des Tropfens zu bestimmen..
Beispiel
Einen Tropfen Öl schweben lassen
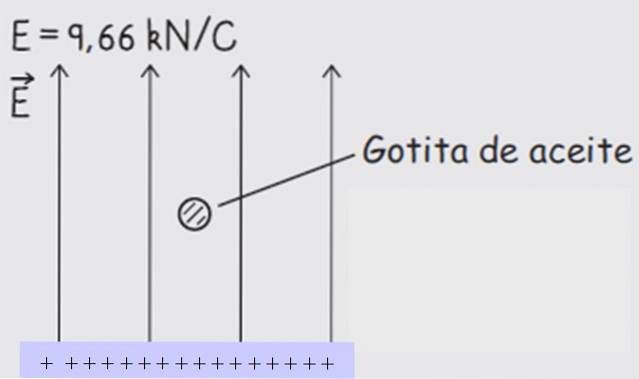
Wir sehen das folgende Beispiel. Ein Öltröpfchen hat eine Dichte ρ = 927 kg / m3 und wird in der Mitte der Elektroden bei ausgeschaltetem elektrischen Feld freigesetzt. Das Tröpfchen erreicht schnell die Endgeschwindigkeit, durch die der Radius bestimmt wird, dessen Wert sich als R = 4,37 x 10 herausstellt-7 m.
Das gleichmäßige Feld ist eingeschaltet, vertikal nach oben gerichtet und hat eine Größe von 9,66 kN / C. Auf diese Weise wird der Tropfen in Ruhe aufgehängt..
Es fragt:
a) Berechnen Sie die Tröpfchenladung
b) Finden Sie heraus, wie oft die Elementarladung in der Ladung des Tropfens enthalten ist.
c) Bestimmen Sie nach Möglichkeit das Vorzeichen der Last.
Lösung für
Zuvor wurde der folgende Ausdruck für einen Tropfen in Ruhe abgeleitet:
q = mg / E.
Bei Kenntnis der Dichte und des Radius des Tropfens wird die Masse des Tropfens bestimmt:
ρ = m / V.
V = (4/3) πR3
Deshalb:
m = ρ.V = ρ. (4/3) πR3= 927 kg / m3. (4/3) π. (4,37 x 10-7 m)3= 3,24 x 10-16 kg
Daher ist die Ladung des Tropfens:
q = mg / E = 3,24 · 10-16 kg x 9,8 m / szwei/ 9660 N = 3,3 × 10-19 C.
Lösung b
Zu wissen, dass die Grundladung e = 1,6 x 10 ist -19 C, die im vorherigen Abschnitt erhaltene Last wird durch diesen Wert geteilt:
n = q / e = 3,3 x 10-19 C /1,6 x 10 -19 C = 2,05
Das Ergebnis ist, dass die Ladung auf dem Tropfen ungefähr doppelt so groß ist (n≈2) wie die Elementarladung. Es ist nicht genau doppelt so hoch, aber diese leichte Diskrepanz ist auf das unvermeidliche Vorhandensein eines experimentellen Fehlers sowie auf die Rundung in jeder der vorherigen Berechnungen zurückzuführen..
Lösung c
Es ist möglich, das Vorzeichen der Ladung zu bestimmen, da die Aussage Informationen über die Richtung des Feldes, das vertikal nach oben gerichtet ist, sowie die Kraft enthält.
Elektrische Feldlinien beginnen immer mit positiven Ladungen und enden mit negativen Ladungen. Daher wird die untere Platte mit einem + -Zeichen und die obere Platte mit einem - -Zeichen geladen (siehe Abbildung 3)..
Da der Tropfen auf die Platte gerichtet ist, die oben vom Feld angetrieben wird, und Ladungen mit entgegengesetztem Vorzeichen anziehen, muss der Tropfen eine positive Ladung haben.
In der Realität ist es nicht einfach, den Tropfen aufgehängt zu halten. Daher verwendete Millikan die vertikalen Verschiebungen (Höhen und Tiefen), die der Tropfen beim Ein- und Ausschalten des Feldes erlebte, sowie die Änderungen der Röntgenladung und der Fahrzeiten, um abzuschätzen, wie viel zusätzliche Ladung der Tropfen erhalten hatte..
Diese erworbene Ladung ist proportional zur Ladung des Elektrons, wie wir bereits gesehen haben, und kann mit den Anstiegs- und Abfallzeiten, der Masse des Tropfens und den Werten von berechnet werden G Y. UND.
Verweise
- Aufgeschlossen. Millikan, der Physiker, der kam, um das Elektron zu sehen. Wiederhergestellt von: bbvaopenmind.com
- Rex, A. 2011. Grundlagen der Physik. Pearson.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. Mcgraw Hügel.
- Amrita. Millikans Öltropfenexperiment. Abgerufen von: vlab.amrita.edu
- Wake Forest College. Millikans Öltropfenexperiment. Wiederhergestellt von: wfu.edu



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.