
Stichprobenfehlerformeln und -gleichungen, Berechnung, Beispiele
Das Stichprobenfehler oder Beispielfehler In der Statistik ist dies die Differenz zwischen dem Mittelwert einer Stichprobe und dem Mittelwert der Gesamtbevölkerung. Stellen wir uns zur Veranschaulichung der Idee vor, dass die Gesamtbevölkerung einer Stadt eine Million Menschen beträgt, von denen die durchschnittliche Schuhgröße gewünscht wird, für die eine Zufallsstichprobe von tausend Menschen gezogen wird.
Die durchschnittliche Größe, die sich aus der Stichprobe ergibt, stimmt nicht unbedingt mit der der Gesamtbevölkerung überein, obwohl der Wert nahe beieinander liegen muss, wenn die Stichprobe nicht voreingenommen ist. Diese Differenz zwischen dem Mittelwert der Stichprobe und dem der Gesamtpopulation ist der Stichprobenfehler.
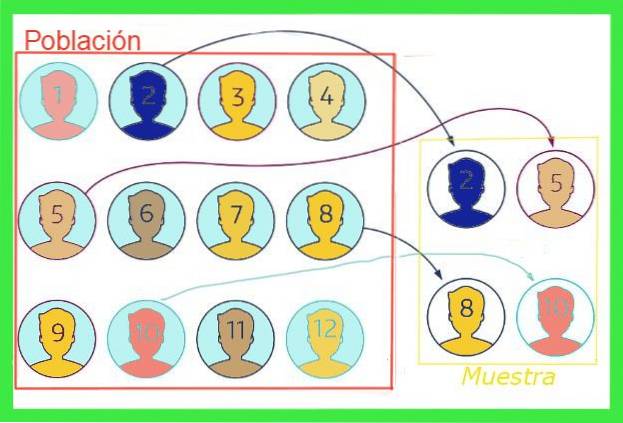
Im Allgemeinen ist der Mittelwert der Gesamtbevölkerung unbekannt, es gibt jedoch Techniken zur Reduzierung dieses Fehlers und Formeln zur Schätzung des Stichprobenfehlergrenze das wird in diesem Artikel ausgesetzt.
Artikelverzeichnis
- 1 Formeln und Gleichungen
- 2 Berechnen des Stichprobenfehlers
- 2.1 Für ein Konfidenzniveau γ
- 3 Beispiele
- 3.1 - Beispiel 1
- 3.2 - Beispiel 2
- 3.3 - Beispiel 3
- 3.4 - Beispiel 4
- 3.5 - Übung 5
- 4 Referenzen
Formeln und Gleichungen
Angenommen, Sie möchten den Durchschnittswert eines bestimmten messbaren Merkmals kennen x in einer Bevölkerung von Größe N., aber wie N. Ist eine große Zahl, ist es nicht möglich, die Studie über die Gesamtbevölkerung durchzuführen, dann fahren wir fort, eine aleatorische Probe von Größe n<
Der Mittelwert der Probe wird mit bezeichnet
Angenommen, sie nehmen m Proben aus der Gesamtbevölkerung N., alle gleich groß n mit Mittelwerten
Diese Mittelwerte sind nicht identisch und liegen alle um den Bevölkerungsmittelwert μ. Das Spielraum für Stichprobenfehler E. gibt die erwartete Trennung der Mittelwerte an
Das Standardfehlergrenze ε Größenprobe n es ist:
ε = σ / √n
wo σ ist die Standardabweichung (die Quadratwurzel der Varianz), die nach folgender Formel berechnet wird:
σ = √ [(x -
Die Bedeutung von Standardfehlergrenze ε ist das Folgende:
Das mittlerer Wert
So berechnen Sie den Stichprobenfehler
Im vorherigen Abschnitt wurde die Formel angegeben, um die zu finden Fehlerbereich Standard einer Stichprobe der Größe n, wobei das Wort Standard angibt, dass es sich um eine Fehlerquote mit 68% iger Sicherheit handelt.
Dies zeigt an, dass viele Proben derselben Größe entnommen wurden n, 68% von ihnen geben Durchschnittswerte an
Es gibt eine einfache Regel namens Regel 68-95-99.7 was uns erlaubt, den Rand von zu finden Stichprobenfehler E. für Konfidenzniveaus von 68%, 95% Y. 99,7% leicht, da dieser Spielraum 1⋅ beträgtε, 2⋅ε und 3⋅ε beziehungsweise.
Für ein gewisses Maß an Vertrauen γ
Wenn er Konfidenzniveau γ ist keine der oben genannten, dann ist der Abtastfehler die Standardabweichung σ multipliziert mit dem Faktor Zγ, welches durch das folgende Verfahren erhalten wird:
1.- Zuerst die Signifikanzniveau α welches berechnet wird aus Konfidenzniveau γ unter Verwendung der folgenden Beziehung: α = 1 - γ
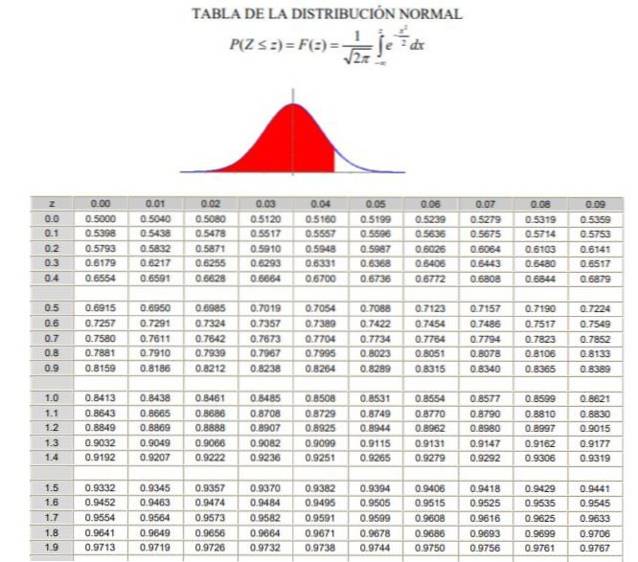
2.- Dann müssen Sie den Wert 1 berechnen - α / 2 = (1 + γ) / 2, Dies entspricht der akkumulierten Normalfrequenz zwischen -∞ und Zγ, in einer normalen oder standardisierten Gaußschen Verteilung F (z), deren Definition in Abbildung 2 zu sehen ist.
3.- Die Gleichung ist gelöst F (Zγ) = 1 - α / 2 anhand der Tabellen der Normalverteilung (kumulativ) F., oder mittels einer Computeranwendung, die die inverse standardisierte Gaußsche Funktion hat F.-1.
Im letzteren Fall haben wir:
Zγ = G.-1(1 - α / 2).
4.- Schließlich wird diese Formel für den Stichprobenfehler mit einem Zuverlässigkeitsniveau angewendet γ:
E = Zγ⋅(σ / √n)
Beispiele
- Beispiel 1
Berechne das Standardfehlerquote im Durchschnittsgewicht einer Stichprobe von 100 Neugeborenen. Die Berechnung des Durchschnittsgewichts war
Lösung
Das Standardfehlerquote es ist ε = σ / √n = (1.500 kg) / √100 = 0,15 kg. Dies bedeutet, dass aus diesen Daten geschlossen werden kann, dass das Gewicht von 68% der Neugeborenen zwischen 2.950 kg und 3,25 kg liegt.
- Beispiel 2
Bestimmen die Marge des Stichprobenfehlers E. und der Gewichtsbereich von 100 Neugeborenen mit einem Konfidenzniveau von 95%, wenn das mittlere Gewicht 3.100 kg mit Standardabweichung beträgt σ = 1.500 kg.
Lösung
Wenn die Regel 68; 95; 99,7 → 1⋅ε; 2⋅ε;; 3⋅ε, du hast:
E = 2 · & epsi; = 2 · 0,15 kg = 0,30 kg
Das heißt, 95% der Neugeborenen haben ein Gewicht zwischen 2.800 kg und 3.400 kg.
- Beispiel 3
Bestimmen Sie den Gewichtsbereich der Neugeborenen aus Beispiel 1 mit einer Konfidenzspanne von 99,7%.
Lösung
Der Stichprobenfehler mit 99,7% Konfidenz beträgt 3 σ / √n, was für unser Beispiel E = 3 · 0,15 kg = 0,45 kg ist. Daraus wird geschlossen, dass 99,7% der Neugeborenen ein Gewicht zwischen 2.650 kg und 3.550 kg haben werden.
- Beispiel 4
Bestimmen Sie den Faktor Zγ für ein Zuverlässigkeitsniveau von 75%. Bestimmen Sie die Fehlerquote bei der Stichprobe mit dieser Zuverlässigkeit für den in Beispiel 1 dargestellten Fall.
Lösung
Das Konfidenzniveau es ist γ = 75% = 0,75, was mit dem zusammenhängt Signifikanzniveau α durch Beziehung γ= (1 - α), so dass das Signifikanzniveau ist α = 1 - 0,75 = 0,25.
Dies bedeutet, dass die kumulative Normalwahrscheinlichkeit zwischen -∞ und Zγ es ist:
P (Z ≤ Zγ ) = 1 - 0,125 = 0,875
Was einem Wert entspricht Zγ 1.1503, wie in Abbildung 3 dargestellt.
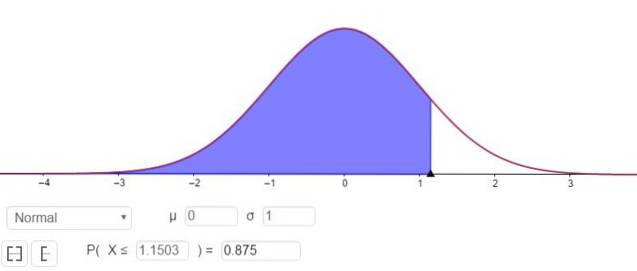
Das heißt, der Abtastfehler ist E = Zγ⋅(σ / √n)= 1.15⋅(σ / √n).
Bei Anwendung auf die Daten aus Beispiel 1 ergibt sich ein Fehler von:
E = 1,15 · 0,15 kg = 0,17 kg
Mit einem Konfidenzniveau von 75%.
- Übung 5
Was ist das Konfidenzniveau, wenn Z.α / 2 = 2,4 ?
Lösung
P (Z ≤ Z.α / 2 ) = 1 - α / 2
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Das Signifikanzniveau ist:
α = 0,0164 = 1,64%
Und schließlich bleibt das Vertrauensniveau:
1- & agr; = 1 - 0,0164 = 100% - 1,64% = 98,36%
Verweise
- Canavos, G. 1988. Wahrscheinlichkeit und Statistik: Anwendungen und Methoden. Mcgraw Hügel.
- Devore, J. 2012. Wahrscheinlichkeit und Statistik für Ingenieurwesen und Wissenschaft. 8 .. Auflage. Engagieren.
- Levin, R. 1988. Statistik für Administratoren. 2 .. Auflage. Prentice Halle.
- Sudman, S. 1982. Fragen stellen: Ein praktischer Leitfaden zur Fragebogendesign. San Francisco. Jossey Bass.
- Walpole, R. 2007. Wahrscheinlichkeit und Statistik für Ingenieurwissenschaften und Naturwissenschaften. Pearson.
- Wonnacott, T.H. und R.J. Wonnacott. 1990. Einführungsstatistik. 5. Aufl. Wiley
- Wikipedia. Stichprobenfehler. Wiederhergestellt von: en.wikipedia.com
- Wikipedia. Fehlermarge. Wiederhergestellt von: en.wikipedia.com


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.