
Lineare Dilatation, was ist das, Formel und Koeffizienten, Beispiel
Das lineare Dilatation tritt auf, wenn ein Objekt aufgrund einer Temperaturschwankung, vorwiegend in einer Dimension, eine Ausdehnung erfährt. Dies liegt an den Eigenschaften des Materials oder seiner geometrischen Form..
Beispielsweise ist in einem Draht oder einer Stange bei einem Temperaturanstieg die Länge die größte Änderung aufgrund der Wärmeausdehnung..

Die Kabel, an denen die Vögel in der vorherigen Abbildung sitzen, leiden unter einer Dehnung, wenn ihre Temperatur steigt. Stattdessen ziehen sie sich zusammen, wenn sie abkühlen. Das gleiche passiert zum Beispiel mit den Stangen, die die Schienen einer Eisenbahn bilden.
Artikelverzeichnis
- 1 Was ist lineare Dilatation??
- 2 Formel der linearen Dilatation und ihr Koeffizient
- 2.1 Längenausdehnungskoeffizient für verschiedene Materialien
- 3 Arbeitsbeispiele für die lineare Ausdehnung
- 3.1 Beispiel 1
- 3.2 Beispiel 2
- 3.3 Beispiel 3
- 3.4 Beispiel 4
- 4 Referenzen
Was ist lineare Dilatation??
In einem festen Material behalten die Atome ihre relativen Positionen mehr oder weniger fest um einen Gleichgewichtspunkt. Aufgrund der thermischen Bewegung schwingen sie jedoch immer um dieselbe.
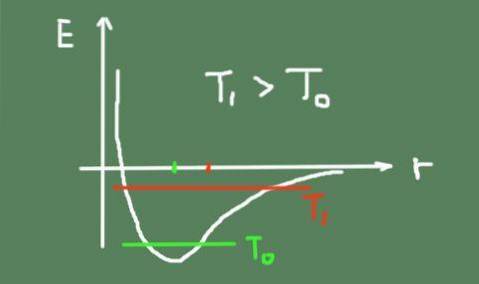
Mit steigender Temperatur nimmt auch die thermische Schwingung zu, wodurch sich die mittleren Schwingungspositionen ändern. Dies liegt daran, dass das Bindungspotential nicht genau parabolisch ist und eine Asymmetrie um das Minimum aufweist.
Unten sehen Sie eine Abbildung, die die chemische Bindungsenergie als Funktion des interatomaren Abstands umreißt. Es zeigt auch die Gesamtenergie der Schwingung bei zwei Temperaturen und wie sich das Schwingungszentrum bewegt.
Formel der linearen Dilatation und ihr Koeffizient
Um die lineare Ausdehnung zu messen, beginnen wir mit einer Anfangslänge L und einer Anfangstemperatur T des Objekts, dessen Ausdehnung gemessen werden soll..
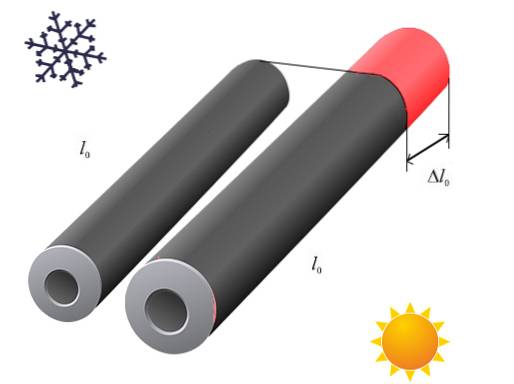
Angenommen, dieses Objekt ist ein Stab, dessen Länge L ist und dessen Querschnittsabmessungen viel kleiner als L sind.
Dieses Objekt wird zuerst einer Temperaturänderung & Dgr; T ausgesetzt, so dass die Endtemperatur des Objekts, sobald das thermische Gleichgewicht mit der Wärmequelle hergestellt ist, T '= T + & Dgr; T ist.
Während dieses Prozesses hat sich auch die Länge des Objekts auf einen neuen Wert L '= L + ΔL geändert, wobei ΔL die Variation der Länge ist.
Der lineare Ausdehnungskoeffizient α ist definiert als der Quotient zwischen der relativen Längenänderung pro Einheitsänderung der Temperatur. Die folgende Formel definiert den linearen Ausdehnungskoeffizienten α::
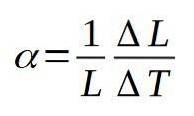
Die Abmessungen des linearen Ausdehnungskoeffizienten sind diejenigen der Umkehrung der Temperatur.
Linearer Ausdehnungskoeffizient für verschiedene Materialien
Als nächstes geben wir eine Liste des linearen Ausdehnungskoeffizienten für einige typische Materialien und Elemente. Der Koeffizient wird bei normalem atmosphärischen Druck basierend auf einer Umgebungstemperatur von 25 ° C berechnet; und sein Wert wird in einem ΔT-Bereich von bis zu 100ºC als konstant angesehen.
Die Einheit des linearen Ausdehnungskoeffizienten ist (° C)-1.
- Stahl: α = 12 ≤ 10-6 (° C)-1
- Aluminium: α = 23 ≤ 10-6 (° C)-1
- Gold: α = 14 ∙ 10-6 (° C)-1
- Kupfer: α = 17 ≤ 10-6 (° C)-1
- Messing: α = 18 ∙ 10-6 (° C)-1
- Eisen: α = 12 ≤ 10-6 (° C)-1
- Glas: α = (7 bis 9) ≤ 10-6 (° C)-1
- Quecksilber: α = 60,4 ≤ 10-6 (° C)-1
- Quarz: α = 0,4 ≤ 10-6 (° C)-1
- Diamant: α = 1,2 ≤ 10-6 (° C)-1
- Blei: α = 30 ≤ 10-6 (° C)-1
- Eichenholz: α = 54 ∙ 10-6 (° C)-1
- PVC: α = 52 ≤ 10-6 (° C)-1
- Kohlefaser: α = -0,8 ≤ 10-6 (° C)-1
- Beton: α = (8 bis 12) ≤ 10-6 (° C)-1
Die meisten Materialien dehnen sich mit steigender Temperatur. Einige spezielle Materialien wie Kohlefasern schrumpfen jedoch mit zunehmender Temperatur..
Arbeitsbeispiele für lineare Dilatation
Beispiel 1
Ein Kupferkabel wird zwischen zwei Masten aufgehängt und hat an einem kühlen Tag bei 20 ° C eine Länge von 12 m. Berechnen Sie den Längengrad an einem heißen Tag bei 35 ° C..
Lösung
Ausgehend von der Definition des linearen Ausdehnungskoeffizienten und in dem Wissen, dass dieser Koeffizient für Kupfer gleich ist: α = 17 ∙ 10-6 (° C)-1
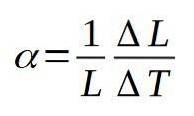
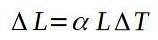
Das Kupferkabel wird länger, aber nur 3 mm. Das heißt, das Kabel reicht von 12.000 m bis 12.003 m.
Beispiel 2
In einer Schmiede verlässt eine Aluminiumstange den Ofen bei 800 Grad Celsius und misst eine Länge von 10,00 m. Sobald es auf die Raumtemperatur von 18 Grad Celsius abgekühlt ist, bestimmen Sie, wie lang der Riegel sein wird.
Lösung
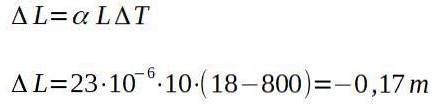
Mit anderen Worten, der Balken hat nach dem Erkalten eine Gesamtlänge von:
9,83 m.
Beispiel 3
Ein Stahlniet hat einen Durchmesser von 0,915 cm. Auf einer Aluminiumplatte wird ein Loch von 0,910 cm gemacht. Dies sind die Anfangsdurchmesser, wenn die Umgebungstemperatur 18 ° C beträgt.
Auf welche Mindesttemperatur muss die Platte erwärmt werden, damit der Niet durch das Loch läuft? Das Ziel dabei ist, dass der Niet fest in der Platte sitzt, wenn das Eisen wieder Raumtemperatur erreicht.
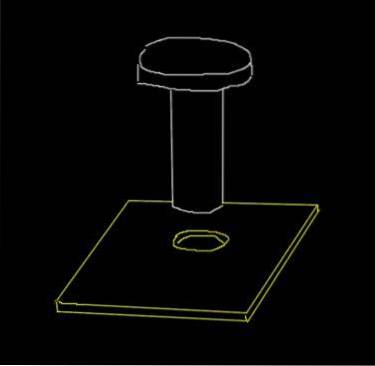
Lösung
Obwohl die Platte eine Oberfläche ist, interessieren wir uns für die Erweiterung des Lochdurchmessers, die eine eindimensionale Größe ist..
Nennen wir D.0 auf den ursprünglichen Durchmesser der Aluminiumplatte und D, auf die sie sich einmal erwärmt hat.
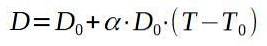
Wenn wir nach der Endtemperatur T suchen, haben wir:
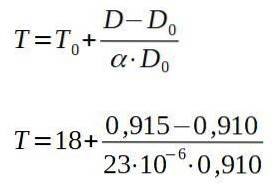
Das Ergebnis der vorherigen Vorgänge ist 257 ° C, was die Mindesttemperatur ist, auf die die Platte erwärmt werden muss, damit der Niet durch das Loch läuft.
Beispiel 4
Der Niet und die Platte aus der vorherigen Übung werden zusammen in einen Ofen gelegt. Bestimmen Sie, bei welcher Mindesttemperatur der Ofen sein muss, damit der Stahlniet durch das Loch in der Aluminiumplatte läuft.
Lösung
In diesem Fall werden sowohl der Niet als auch das Loch erweitert. Der Ausdehnungskoeffizient von Stahl beträgt jedoch α = 12 ∙ 10-6 (° C)-1, während die von Aluminium α = 23 ∙ 10 ist-6 (° C)-1 .
Wir suchen dann nach einer Endtemperatur T, so dass beide Durchmesser zusammenfallen.
Wenn wir den Niet 1 und die Aluminiumplatte 2 nennen, suchen wir nach einer Endtemperatur T, so dass D.1 = D.zwei.
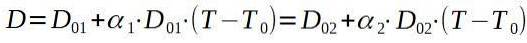
Wenn wir nach der Endtemperatur T auflösen, bleibt uns Folgendes übrig:
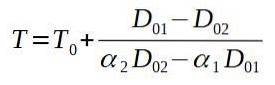
Dann setzen wir die entsprechenden Werte.
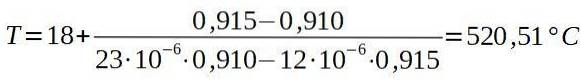
Die Schlussfolgerung ist, dass der Ofen mindestens 520,5 ° C haben muss, damit der Niet durch das Loch in der Aluminiumplatte läuft.
Verweise
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. Sechste Ausgabe. Prentice Hall. 238-249.
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mac Graw Hill. 422-527.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.