Unterschied von Würfelformeln, Gleichungen, Beispielen, Übungen

Das Unterschied der Würfel ist ein binomialer algebraischer Ausdruck der Form a³ - b³, wobei die Begriffe a und b reelle Zahlen oder algebraische Ausdrücke verschiedener Typen sein können. Ein Beispiel für einen Unterschied von Würfeln ist: 8 - x³, da 8 kann als 2 geschrieben werden³.

Geometrisch können wir uns einen großen Würfel mit Seite a vorstellen, von dem der kleine Würfel mit Seite b abgezogen wird, wie in Abbildung 1 dargestellt:

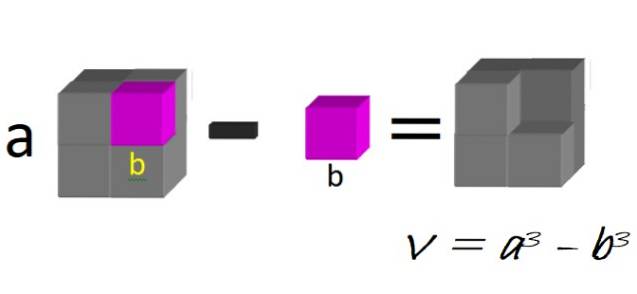
Das Volumen der resultierenden Figur ist genau ein Unterschied der Würfel:

V = a³ - b³

Um einen alternativen Ausdruck zu finden, wird beobachtet, dass diese Figur in drei Prismen zerlegt werden kann, wie unten gezeigt:

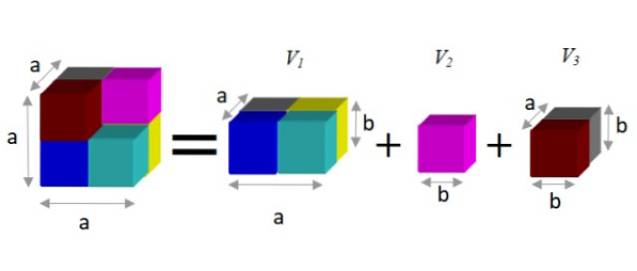
Ein Prisma hat ein Volumen, das sich aus dem Produkt seiner drei Dimensionen ergibt: Breite x Höhe x Tiefe. Auf diese Weise ergibt sich Folgendes:

V = a³ - b³ = a^zwei.b + b³ + a.b.^zwei

Der Faktor b es ist rechts üblich. Darüber hinaus gilt in der oben gezeigten Abbildung insbesondere Folgendes:

b = (a / 2) ⇒ a = b + b

Daher kann gesagt werden, dass: b = a - b. So:

zu³ - b³ = b (a^zwei + b^zwei +a.b) = (a-b) (a^zwei + a.b + b^zwei)

Diese Art, den Unterschied der Würfel auszudrücken, wird sich in vielen Anwendungen als sehr nützlich erweisen und wäre auf die gleiche Weise erhalten worden, selbst wenn sich die Seite des fehlenden Würfels in der Ecke von b = a / 2 unterschieden hätte.

Beachten Sie, dass die zweite Klammersieht dem bemerkenswerten Produkt des Quadrats der Summe sehr ähnlich, aber Der Kreuzterm wird nicht mit 2 multipliziert. Der Leser kann die rechte Seite entwickeln, um zu überprüfen, ob sie tatsächlich erhalten wurde zu³ - b³.

Artikelverzeichnis

• 1 Beispiele
  • 1.1 Berücksichtigung eines Würfelunterschieds
• 2 Übung gelöst
  • 2.1 Übung 1
  • 2.2 Übung 2
• 3 Referenzen

Beispiele

Es gibt verschiedene Unterschiede bei Würfeln:

1 - m⁶

zu⁶b³ - 8z¹²Y.⁶

(1/125) .x⁶ - 27 und⁹

Lassen Sie uns jeden von ihnen analysieren. Im ersten Beispiel kann die 1 als 1 = 1 geschrieben werden³ und der Begriff m⁶ bleibt: (m^zwei)³. Beide Begriffe sind perfekte Würfel, daher ist ihr Unterschied:

1 - m⁶ = 1³ - (m^zwei)³

Im zweiten Beispiel werden die Begriffe neu geschrieben:

zu⁶b³ = (a^zweib)³

8z¹²Y.⁶ = 2³ (z⁴)³ (Y.^zwei)³ = (2z⁴Y.^zwei)³

Der Unterschied dieser Würfel ist :.^zweib)³ - (2z⁴Y.^zwei)³.

Schließlich ist der Bruch (1/125) (1/5³), x⁶ = (x^zwei)³, 27 = 3³ und und⁹ = (und³)³. Wenn Sie all dies in den ursprünglichen Ausdruck einsetzen, erhalten Sie:

(1/125) .x⁶  - 27y⁹ = [(1/5) (x^zwei)]³ - (3J³)³

Berücksichtigung eines Unterschieds von Würfeln

Das Berücksichtigen der Würfeldifferenz vereinfacht viele algebraische Operationen. Dazu reicht es aus, die oben abgeleitete Formel zu verwenden:

Das Verfahren zum Anwenden dieser Formel besteht nun aus drei Schritten:

- Zunächst wird die Kubikwurzel jedes der Terme der Differenz erhalten.

- Dann werden das Binomial und das Trinomial konstruiert, die auf der rechten Seite der Formel erscheinen.

- Schließlich werden das Binomial und das Trinomial ersetzt, um die endgültige Faktorisierung zu erhalten.

Lassen Sie uns die Verwendung dieser Schritte mit jedem der oben vorgeschlagenen Würfeldifferenzbeispiele veranschaulichen und so das faktorisierte Äquivalent erhalten.

Beispiel 1

Faktor der Ausdruck 1 - m⁶   Befolgen Sie die beschriebenen Schritte. Wir beginnen damit, den Ausdruck als 1 - m umzuschreiben⁶ = 1³ - (m^zwei)³ um die jeweiligen Kubikwurzeln jedes Begriffs zu extrahieren:

Als nächstes werden das Binomial und das Trinom konstruiert:

a = 1

b = m^zwei

Dann:

a - b = 1 - m^zwei

 (zu^zwei +a.b + b^zwei) = 1^zwei + 1.m.^zwei + (m^zwei)^zwei = 1 + m^zwei + m⁴

 Schließlich wird es in der Formel a eingesetzt³ - b³ = (a-b) (a^zwei +a.b + b^zwei):

1 - m⁶ = (1 - m^zwei) (1 + m^zwei + m⁴)

Beispiel 2

Faktorisieren:

zu⁶b³ -8z¹²Y.⁶ = (a^zweib)³ - (2z⁴Y.^zwei)³

Da es sich um perfekte Würfel handelt, sind die Kubikwurzeln unmittelbar: a^zweib und 2z⁴Y.^zwei, daher folgt daraus:

- Binomial: a^zweib - 2z⁴Y.^zwei

- Trinomial: (a^zweib)^zwei + zu^zweib. 2z⁴Y.^zwei + (zu^zweib + 2z⁴Y.^zwei)^zwei

 Und jetzt ist die gewünschte Faktorisierung konstruiert:

zu⁶b³ -8z¹²Y.⁶ = (a^zweib - 2z⁴Y.^zwei). [(zu^zweib)^zwei + zu^zweib. 2z⁴Y.^zwei + (zu^zweib + 2z⁴Y.^zwei)^zwei] =

= (a^zweib - 2z⁴Y.^zwei). [zu⁴b^zwei + 2 ..^zweib.z.⁴Y.^zwei + (zu^zweib + 2z⁴Y.^zwei)^zwei]]

Im Prinzip ist das Factoring fertig, aber es ist oft notwendig, jeden Begriff zu vereinfachen. Dann entwickeln wir das bemerkenswerte Produktquadrat einer Summe, das am Ende erscheint, und fügen dann ähnliche Begriffe hinzu. Denken Sie daran, dass das Quadrat einer Summe ist:

(x + y)^zwei = x^zwei + 2xy + und^zwei

Das bemerkenswerte Produkt auf der rechten Seite ist wie folgt entwickelt:

(zu^zweib + 2z⁴Y.^zwei)^zwei = a⁴b^zwei + 4 ..^zweib.z.⁴Y.^zwei + 4z⁸Y.⁴

 Einsetzen der Expansion, die bei der Faktorisierung der Differenz der Würfel erhalten wurde:

zu⁶b³ -8z¹²Y.⁶ = (a^zweib - 2z⁴Y.^zwei). [zu⁴b^zwei + 2 ..^zweib.z.⁴Y.^zwei + zu⁴b^zwei + 4 ..^zweib.z.⁴Y.^zwei + 4z⁸Y.⁴] =

Wenn wir schließlich gleiche Terme gruppieren und die numerischen Koeffizienten berücksichtigen, die alle gerade sind, erhalten wir:

(zu^zweib - 2z⁴Y.^zwei). [2a⁴b^zwei + 6 ..^zweib.z.⁴Y.^zwei + 4z⁸Y.⁴] = 2 (a^zweib - 2z⁴Y.^zwei). [zu⁴b^zwei + 3 ..^zweib.z.⁴Y.^zwei + 2z⁸Y.⁴]]

Beispiel 3

Faktor (1/125) .x⁶  - 27y⁹ es ist viel einfacher als der vorherige Fall. Zunächst werden die Äquivalente von a und b identifiziert:

a = (1/5) x^zwei

b = 3y³

Dann werden sie direkt in die Formel eingesetzt:

(1/125) .x⁶  - 27y⁹ = [(1/5) x^zwei - 3y³]. [(1/25) x⁴ + (3/5) x^zweiY.³ + 9y⁶]]

Übung gelöst

Der Unterschied der Würfel hat, wie gesagt, eine Vielzahl von Anwendungen in der Algebra. Mal sehen:

Übung 1

Lösen Sie die folgenden Gleichungen:

a) x⁵ - 125 x^zwei = 0

b) 64 - 729 x³ = 0

Lösung für

Zunächst wird die Gleichung folgendermaßen berücksichtigt:

x^zwei (x³ - 125) = 0

Da 125 ein perfekter Würfel ist, werden die Klammern als Differenz der Würfel geschrieben:

x^zwei . (x³ - 5³) = 0

Die erste Lösung ist x = 0, aber wir finden mehr, wenn wir x tun³ - 5³ = 0, dann:

x³ = 5³ → x = 5

Lösung b

Die linke Seite der Gleichung wird als 64 - 729 x umgeschrieben³ = 4³ - (9x)³. Deshalb:

4³ - (9x)³ = 0

Da der Exponent der gleiche ist:

9x = 4 → x = 9/4

Übung 2

Faktor der Ausdruck:

(x + y)³ - (x - y)³

Lösung

Dieser Ausdruck ist ein Unterschied von Würfeln, wenn wir in der Faktorisierungsformel Folgendes feststellen:

a = x + y

b = x-y

Dann wird zuerst das Binomial konstruiert:

a - b = x + y - (x - y) = 2y

Und jetzt das Trinom:

zu^zwei + a.b + b^zwei = (x + y)^zwei + (x + y) (x-y) + (x-y)^zwei

Bemerkenswerte Produkte werden entwickelt:

(x + y)^zwei = x^zwei + 2xy + und^zwei

(x + y) (x-y) = x^zwei- Y.^zwei

(x-y)^zwei = x^zwei - 2xy + und^zwei

Als nächstes müssen Sie ähnliche Begriffe ersetzen und reduzieren:

zu^zwei + a.b + b^zwei = x^zwei + 2xy + und^zwei+ x^zwei- Y.^zwei+ x^zwei - 2xy + und^zwei = 3x^zwei + Y.^zwei

Faktorisierung führt zu:

(x + y)³ - (x - y)³ = 2y. (3x^zwei + Y.^zwei)

Verweise

1. Baldor, A. 1974. Algebra. Editorial Cultural Venezolana S.A..
2. CK-12-Stiftung. Summe und Differenz der Würfel. Wiederhergestellt von: ck12.org.
3. Khan Akademie. Berücksichtigung von Würfelunterschieden. Wiederhergestellt von: es.khanacademy.org.
4. Mathe macht Spaß für Fortgeschrittene. Unterschied von zwei Würfeln. Wiederhergestellt von: mathsisfun.com
5. UNAM. Berücksichtigung eines Unterschieds von Würfeln. Wiederhergestellt von: dcb.fi-c.unam.mx.