
Freikörperbild, wie es geht, Beispiele, Übung
EIN Freikörperdiagramm, Isoliertes Körperdiagramm oder Kraftdiagramm ist ein Diagramm, in dem die auf einen Körper einwirkenden Kräfte durch Pfeile dargestellt werden.
Stellen Sie sicher, dass Sie in das Diagramm aufgenommen werden alle die Kräfte, die auf das Objekt wirken, und da es sich um eine Vektorgröße handelt, ist der Pfeil dafür verantwortlich, seine Richtung und seinen Sinn anzuzeigen, während seine Länge eine Vorstellung vom Modul oder der Intensität liefert.
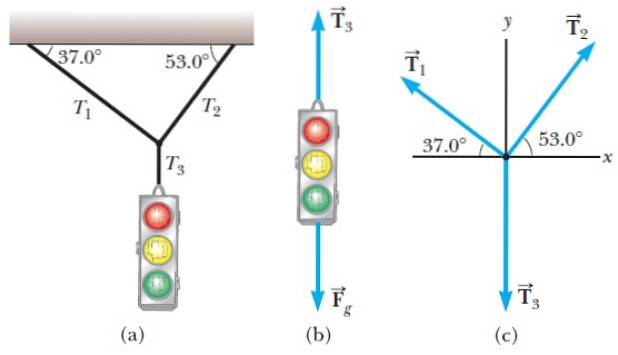
In Abbildung 1 haben wir ein Beispiel für ein Freikörperdiagramm, das wir analysieren werden.
Die Situation ist wie folgt: Eine Ampel hängt in Ruhe an einigen Kabeln (Abbildung 1a). Zwei Kräfte wirken darauf, eine ist diejenige, die von der Erde ausgeübt wird, was Gewicht ist. Im Diagramm wird es als bezeichnet F.G und wirkt senkrecht nach unten.
Die andere Kraft ist die Spannung in der vertikalen Saite, die genannt wird T.3 und das geht in vertikaler Richtung nach oben, hält die Ampel und verhindert, dass sie zu Boden fällt.
Wenn ein Problem mehr als ein Objekt hat, muss für jedes ein einzelnes Diagramm erstellt werden..
Der Knoten zwischen den geneigten Seilen und dem Seil, das die Ampel hält, wird als Punktobjekt betrachtet, und sein Freikörperdiagramm ist in Abbildung 1c dargestellt. Beachten Sie, dass für den Knoten die Spannung T.3 ist nach unten gerichtet.
Es ist wichtig zu beachten, dass die vom Objekt auf andere Körper ausgeübten Kräfte nicht im Freikörperdiagramm erscheinen sollten, sondern nur diejenigen, die darauf einwirken.
Artikelverzeichnis
- 1 Beispiele für Freikörperdiagramme
- 1.1 Eine Person, die einen Kofferraum oder Container zieht
- 1.2 Ein Block, der eine schiefe Ebene hinuntergleitet
- 1.3 Atwoods Maschine
- 2 Übung gelöst
- 2.1 Lösung
- 3 Referenzen
Beispiele für Freikörperdiagramme
Das Freikörperdiagramm ermöglicht die Anwendung der Newtonschen Gesetze und bestimmt mit ihnen den Bewegungszustand oder den Rest des Objekts, auf das die Kräfte wirken. Im Fall der gezeigten Ampel können wir den Wert der Spannungen in den Kabeln bestimmen, die die Ampel halten, wobei wir das Gewicht dieser kennen.
Sobald diese Daten bekannt sind, werden geeignete Kabel ausgewählt, um die Ampel aufzuhängen, und die ihre Funktion erfüllen, ohne zusammenzufallen.
Freikörperdiagramme werden verwendet, um verschiedene alltägliche Situationen zu beschreiben, wie diese:
Eine Person, die einen Kofferraum oder Container zieht
Es ist sehr häufig, dass Menschen schwere Gegenstände wie den in der Abbildung gezeigten Behälter tragen müssen. Dazu müssen sie eine Kraft ausüben F. über den Container, Das ist in diesem Beispiel horizontal und rechts, das ist die Bewegungsrichtung.
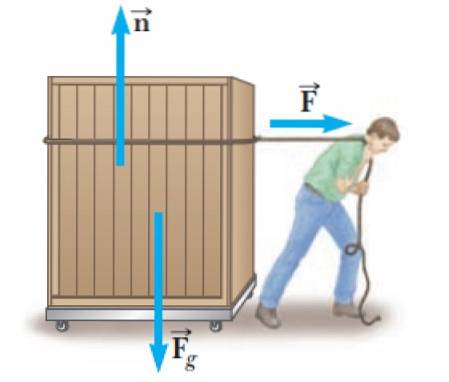
Aber dies ist nicht die einzige Kraft, die auf ihn einwirkt, es gibt auch die normale n, ausgeübt durch die flache Oberfläche der fahrbaren Plattform. Und schließlich ist da noch das Gewicht: F.G, senkrecht nach unten gerichtet.
Die Normale ist eine Kraft, die entsteht, wenn zwei Oberflächen in Kontakt stehen und immer senkrecht zu der Oberfläche ist, die sie ausübt. In diesem Fall übt die fahrbare Plattform eine Normalität auf den Container aus.
Ein Block, der eine schiefe Ebene hinuntergleitet
Bei einigen Schreibtischen ist der Tisch leicht geneigt, damit Sie sich leichter Notizen machen und lesen können. Es hat auch einen Stifthalterschlitz, aber wir haben alle den Bleistift aus dem Schlitz auf den Tisch gelegt und gesehen, wie er auf den Tisch gleitet.
Welche Kräfte wirken auf den Bleistift??
Die gleichen, die auf den im folgenden Freikörperdiagramm gezeigten Block wirken:
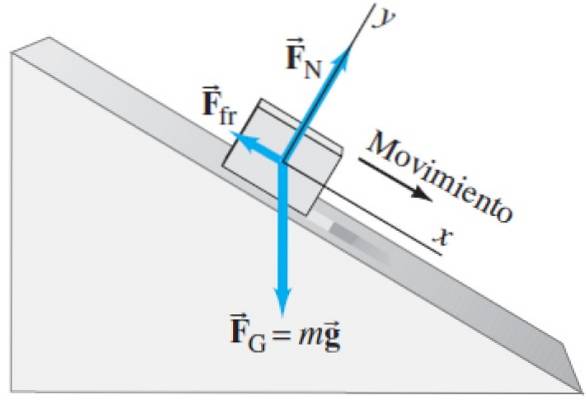
Das Normale F.N. ist die Kraft, die die Tischoberfläche auf den unterstützten Bleistift oder Block ausübt. Im Gegensatz zum vorherigen Beispiel ist die Normalen nicht vertikal, sondern schräg. Denken Sie daran, dass die Normalen die Kraft sind, die der Tisch auf den Block ausübt und senkrecht dazu steht. Wenn der Tisch gekippt wird, auch der normale.
Wie immer das Gewicht F.G ist vertikal, unabhängig von der Neigung des Systems.
Und schließlich haben wir eine neue Kraft, die kinetische Reibung ist F.fr zwischen dem Tisch und dem Bleistift oder Block. Reibung ist auch eine Kontaktkraft, aber im Gegensatz zu normal ist sie eine tangentiale (parallele) Kraft zur Oberfläche. Beachten Sie auch, dass es immer in die entgegengesetzte Richtung zur Bewegung gerichtet ist..
Atwoods Maschine
Die Atwood-Maschine ist eine einfache Maschine, die aus einer leichten, reibungsfreien Riemenscheibe auf der Schiene besteht, durch die ein leichtes und nicht dehnbares Seil verläuft.
Daran hängen zwei Objekte der Masse m1 und Mzwei. Wenn eines der Objekte nach oben geht, geht das andere nach unten, wie in Abbildung 4a gezeigt:
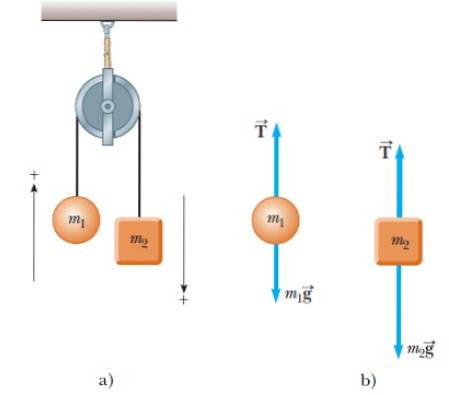
Da es zwei Objekte gibt, wird für jedes einzeln ein Freikörperdiagramm erstellt. Für beide Objekte gibt es nur zwei Kräfte: die Spannung in der Saite T. und die jeweiligen Gewichte.
In der Figur wird jedes Gewicht direkt als Produkt aus Masse und Beschleunigung ausgedrückt. Die Spannung ist ihrerseits immer vertikal entlang des gespannten Seils gerichtet.
Übung gelöst
Wenden Sie die Newtonschen Gesetze an, um die Beschleunigung zu bestimmen, mit der sich die Massen von der im vorherigen Abschnitt gezeigten Atwood-Maschine bewegen.
Lösung
Newtons zweites Gesetz besagt, dass die Summe der Kräfte gleich dem Produkt aus Masse und Beschleunigung ist.
Die Vorzeichenkonvention in jeder Masse kann unterschiedlich sein, daher werden wir Bewegung als positiven Sinn nehmen, wie in der Grafik angegeben, die erste Masse steigt und die zweite fällt.
Bei einigen Problemen liefert die Anweisung keine Informationen, dann müssen die Vorzeichen willkürlich zugewiesen werden, und wenn das Ergebnis der Beschleunigung negativ ist, bewegt sich das Massensystem in die entgegengesetzte Richtung zu der ursprünglich angenommenen.
-Für Masse 1 (steigt):
T - m1g = m1zu
-Für Masse 2 (niedrig):
-T + mzweig = mzweizu
Beide Gleichungen bilden ein lineares Gleichungssystem zweier Unbekannter. Da die Spannung in jeder Gleichung mit einem anderen Vorzeichen erscheint, fügen wir sie einfach Term für Term hinzu und die Spannung wird aufgehoben:
mzweig - m1g = m1a + mzweizu
a = mzweig - m1g / (m1 + mzwei)
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
- Serway, R., Vulle, C. 2011. College Physics. 9. Aufl. Lernen einbinden.
- Tipler, P. (2006) Physik für Wissenschaft und Technologie. 5. Aufl. Band 1. Editorial Reverté.
- Tippens, P. 2011. Physik: Konzepte und Anwendungen. 7. Auflage. Mcgraw Hügel

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.