Bevor du es weißt wie viele Hundertstel passen in ein Zehntel Die Konzepte der Zehntel und Hundertstel sollten geklärt werden. Das Konzept, aus dem diese Wörter hervorgehen, ist das des Dezimalbruchs.
Die Verwendung von Dezimalbrüchen ist häufiger als Sie sich vorstellen können. Sie können von den Preisen eines Produkts in einem Geschäft bis zum Gewicht eines Obstkorbs im Supermarkt angewendet werden.
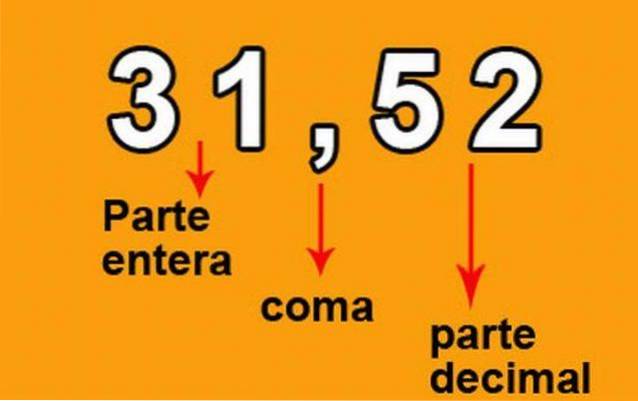
Das Komma im Bild wird als "Dezimalpunkt" bezeichnet, in der englischen und nordamerikanischen Bibliographie wird jedoch anstelle des Kommas ein "Punkt" verwendet.
Artikelverzeichnis
Ein Dezimalbruch ist ein Bruch, dessen Nenner 10, 100, 1.000, 10.000 oder eine andere Potenz von 10 ist, daher das Wort Dezimal. Zum Beispiel sind 2 / 10.000, 53/10, 2.781 / 100, 321 / 1.000 Dezimalbrüche.
Wenn ein Dezimalbruch geschrieben wird, wird der Nenner weggelassen und ein Vorzeichen (ein Dezimalpunkt) wird gesetzt, um den Wert der Zahl anzuzeigen.
In der Zahl des Zählers und rechts vom Komma müssen so viele Zahlen stehen, wie der entsprechende Nenner Nullen enthält.
- 2 / 10.000 würden als 0,0002 geschrieben.
- 53/10 würde als 5.3 geschrieben werden.
- 2,781 / 100 wird als 27,81 geschrieben.
- 321 / 1.000 wird als 0,321 geschrieben.
Andererseits beträgt der Bruch, der die Zahl im vorherigen Bild darstellt, 3,152 / 100, da die Zahl zwei Ziffern rechts vom Dezimalpunkt hat.
Die Zahl links vom Komma wird als "ganzzahliger Teil" bezeichnet, während die Zahl rechts als "Dezimalteil" bezeichnet wird..
So wie der ganzzahlige Teil einer Zahl aus Einheiten besteht, Zehner und Hunderter, die von rechts nach links benannt sind, besteht der Dezimalteil auch aus Zehntel, Hundertstel und Tausendstel von links nach rechts.
Die Zehntel entsprechen der ersten Ziffer rechts vom Dezimalpunkt, und der Nenner seines Dezimalbruchs ist 10. Beispielsweise entsprechen 3 Zehntel (0,3) 3/10.
Auf der anderen Seite entspricht 46/10 46 Zehnteln und seine Dezimalzahl beträgt 4,6, was auch als 4 Einheiten mit 6 Zehnteln gelesen werden kann.
Gleiches gilt für Hundertstel (zweite Ziffer rechts vom Dezimalpunkt) und Tausendstel (dritte Ziffer rechts vom Dezimalpunkt), deren Nenner im Dezimalbruch 100 bzw. 1.000 sind..
Mit dem, was oben geschrieben steht, ist bekannt, dass ein Zehntel gleich 1/10 ist und dass ein Hundertstel 1/100 ist. In Dezimalschreibweise haben wir, dass ein Zehntel 0,1 und ein Hundertstel 0,01 ist.
Der Schlüssel zur Beantwortung dieser Frage besteht darin, zu wissen, wie oft ein Hundertstel mit sich selbst addiert werden muss, sodass das Ergebnis nur ein Zehntel beträgt.
Wenn wir die Berechnungen durchführen, wird man sehen, dass es notwendig ist, ein Hundertstel zehnmal mit sich selbst zu addieren, um ein Zehntel zu erhalten.
Daher passen 10 Hundertstel in ein Zehntel.
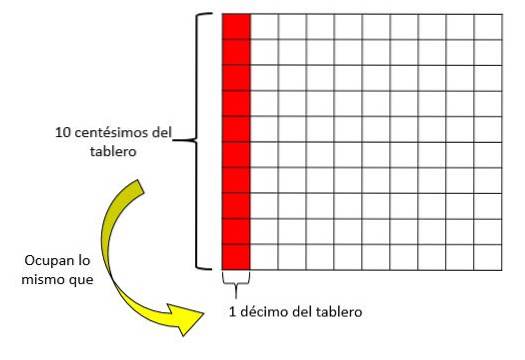
Ein anderer Prozess, mit dem wir herausfinden können, wie viele Hundertstel in ein Zehntel passen, ist der folgende: Ein Brett mit 100 Quadraten wird genommen, dann repräsentiert 1 Quadrat auf dem Brett ein Hundertstel, während jede Spalte (oder Zeile) von 10 Quadraten 1 Zehntel repräsentiert des Vorstandes.
Um eine Zeile (1 Zehntel) zu füllen, sind 10 Quadrate (10 Hundertstel) erforderlich..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.