
Viereckige Elemente, Eigenschaften, Klassifizierung, Beispiele
EIN Viereck ist ein Polygon mit vier Seiten und vier Eckpunkten. Ihr gegenüberliegende Seiten sind diejenigen, die keine gemeinsamen Eckpunkte haben, während sie es sind aufeinanderfolgende Seiten diejenigen mit einem gemeinsamen Scheitelpunkt.
In einem Viereck sind sie angrenzende Winkel diejenigen, die eine Seite teilen, während die entgegengesetzte Winkel Sie haben keine gemeinsamen Seiten. Ein weiteres wichtiges Merkmal eines Vierecks ist die Summe seiner vier Innenwinkel ist doppelt so groß wie der ebene Winkel, dh 360º oder 2π Bogenmaß.
Diagonalen sind die Segmente, die einen Scheitelpunkt mit seinem Gegenteil verbinden, und in einem gegebenen Viereck kann von jedem Scheitelpunkt eine einzelne Diagonale gezeichnet werden. Die Gesamtzahl der Diagonalen in einem Viereck beträgt zwei.
Vierecke sind Figuren, die der Menschheit seit der Antike bekannt sind. Die archäologischen Aufzeichnungen sowie die heute erhaltenen Konstruktionen bestätigen dies..
Ebenso haben die Vierecke auch heute noch eine wichtige Präsenz im täglichen Leben aller. Der Leser kann dieses Formular auf dem Bildschirm finden, auf dem der Text gerade gelesen wird, auf Fenstern, Türen, Autoteilen und unzähligen anderen Stellen..
Artikelverzeichnis
- 1 Klassifikation der Vierecke
- 1.1 Arten von Parallelogrammen
- 2 Trapez
- 2.1 Arten von Trapezoiden
- 3 Parallelogramm
- 3.1 Fläche eines Parallelogramms
- 3.2 Diagonalen eines Parallelogramms
- 3.3 Gesetz der Parallelogramme
- 4 Rechteck
- 4.1 Diagonalen eines Rechtecks
- 5 Quadrat
- 6 Raute
- 7 Beispiele
- 7.1 Beispiel 1
- 7.2 Beispiel 2
- 7.3 Beispiel 3
- 8 Übungen gelöst
- 8.1 - Übung 1
- 8.2 - Übung 2
- 9 Referenzen
Viereckige Klassifikation
Entsprechend der Parallelität der gegenüberliegenden Seiten werden die Vierecke wie folgt klassifiziert:
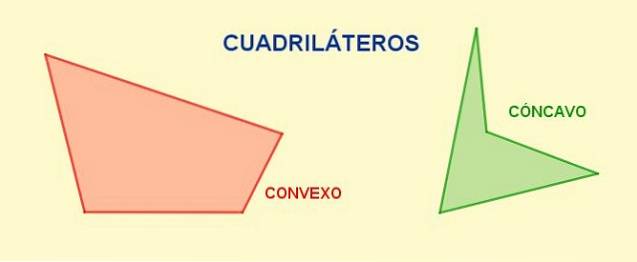
- Trapez, wenn es keine Parallelität gibt und das Viereck konvex ist.
- Trapez, wenn es Parallelität zwischen einem einzelnen Paar gegenüberliegender Seiten gibt.
- Parallelogramm, wenn seine gegenüberliegenden Seiten zwei mal zwei parallel sind.
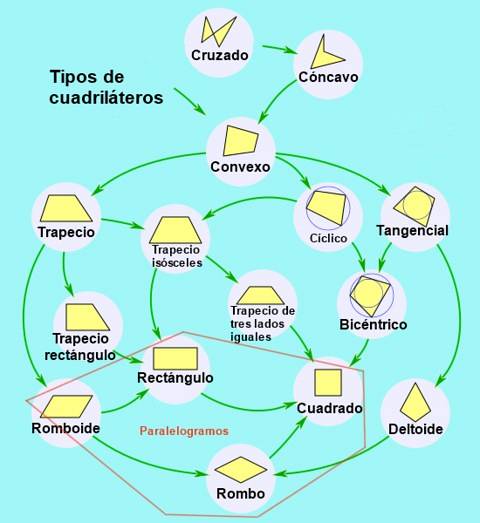
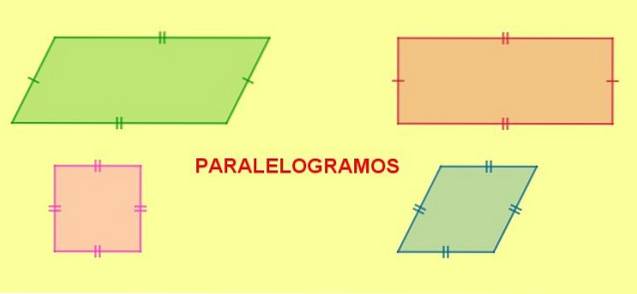
Arten von Parallelogrammen
Parallelogramme können wiederum nach ihren Winkeln und Seiten wie folgt klassifiziert werden:
- Rechteck, ist das Parallelogramm, dessen vier Innenwinkel gleich groß sind. Die Innenwinkel eines Rechtecks bilden einen rechten Winkel (90º)..
- Quadrat, ist ein Rechteck mit vier gleich großen Seiten.
- Diamant, ist das Parallelogramm mit seinen vier gleichen Seiten, aber unterschiedlichen benachbarten Winkeln.
- Rhomboid, Parallelogramm mit verschiedenen benachbarten Winkeln.
Trapez
Das Trapez ist ein konvexes Viereck mit zwei parallelen Seiten.
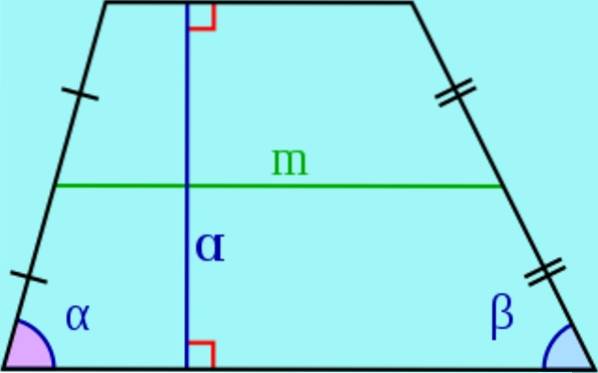
- In einem Trapez werden die parallelen Seiten genannt Basen und die Nicht-Parallelen werden aufgerufen seitlich.
- Das Höhe eines Trapezes ist der Abstand zwischen den beiden Basen, dh die Länge eines Segments mit Enden an den Basen und senkrecht zu diesen. Dieses Segment wird auch als Trapezhöhe bezeichnet..
- Das Median ist das Segment, das die Mittelpunkte der Seitenteile verbindet. Es kann gezeigt werden, dass der Median parallel zu den Basen des Trapezes verläuft und seine Länge gleich der Halbsumme der Basen ist.
- Die Fläche eines Trapezes ist seine Höhe multipliziert mit der Halbsumme der Basen:
Fläche eines Trapezes = Höhe * (Basis 1 + Basis 2) / 2
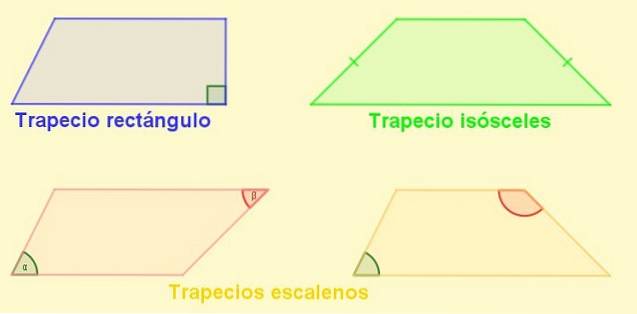
Arten von Trapezoiden
-Rechteck Trapez: Ist der mit einer seitlichen Senkrechten zu den Basen. Diese Seite ist auch die Höhe des Trapezes.
-Trapez gleichschenklig: Die mit gleich langen Seiten. In einem gleichschenkligen Trapez sind die Winkel neben den Basen gleich.
-Scalene Trapez: Die mit ihren Seiten unterschiedlicher Länge. Seine entgegengesetzten Winkel können einer spitz und der andere stumpf sein, aber es kann auch vorkommen, dass beide stumpf oder beide spitz sind..
Parallelogramm
Das Parallelogramm ist ein Viereck, dessen gegenüberliegende Seiten zwei mal zwei parallel sind. In einem Parallelogramm sind die entgegengesetzten Winkel gleich und die benachbarten Winkel sind ergänzend, oder mit anderen Worten, die benachbarten Winkel addieren sich zu 180º.
Wenn ein Parallelogramm einen rechten Winkel hat, sind es auch alle anderen Winkel, und die resultierende Zahl wird aufgerufen Rechteck. Wenn das Rechteck jedoch auch benachbarte Seiten gleicher Länge hat, sind alle Seiten gleich und die resultierende Zahl ist a Quadrat.
Wenn ein Parallelogramm zwei benachbarte Seiten gleicher Länge hat, sind alle Seiten gleich lang und die resultierende Zahl ist a Diamant.
Die Höhe eines Parallelogramms ist ein Segment mit Enden an den gegenüberliegenden Seiten und senkrecht zu diesen..
Fläche eines Parallelogramms
Die Fläche eines Parallelogramms ist das Produkt aus Basis und Höhe, wobei die Basis eine Seite senkrecht zur Höhe ist (Abbildung 6)..
Fläche eines Parallelogramms = Basis x Höhe = a. h
Diagonalen eines Parallelogramms
Das Quadrat der Diagonale, das von einem Scheitelpunkt ausgeht, ist gleich der Summe der Quadrate der beiden Seiten, die an den Scheitelpunkt angrenzen, plus dem Doppelprodukt dieser Seiten durch den Kosinus des Winkels dieses Scheitelpunkts:
F.zwei = azwei + dzwei + 2 und Cos (α)
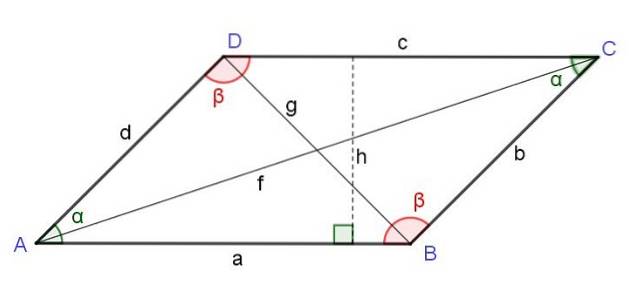
Das Quadrat der Diagonale gegenüber dem Scheitelpunkt eines Parallelogramms ist gleich der Summe der Quadrate der beiden Seiten neben dem Scheitelpunkt und subtrahiert das Doppelprodukt dieser Seiten durch den Kosinus des Winkels dieses Scheitelpunkts:
Gzwei = azwei + dzwei - 2 und Cos (α)
Gesetz der Parallelogramme
In jedem Parallelogramm ist die Summe der Quadrate seiner Seiten gleich der Summe der Quadrate der Diagonalen:
zuzwei + bzwei + czwei + dzwei = fzwei + Gzwei
Rectangle
Das Rechteck ist ein Viereck, dessen gegenüberliegende Seiten zwei mal zwei parallel sind und das auch einen rechten Winkel hat. Mit anderen Worten, das Rechteck ist eine Art Parallelogramm mit einem rechten Winkel. Für das Parallelogramm, Das Rechteck hat gegenüberliegende Seiten gleicher Länge a = c und b = d.
Aber wie in jedem Parallelogramm sind die benachbarten Winkel ergänzend und die entgegengesetzten Winkel gleich. Da das Rechteck einen rechten Winkel hat, bildet es notwendigerweise rechte Winkel in den anderen drei Winkeln. Nämlich In einem Rechteck messen alle Innenwinkel 90º oder π / 2 Bogenmaß.
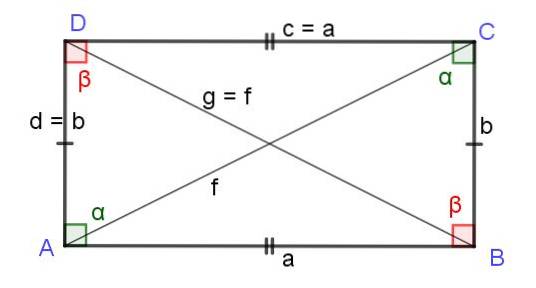
Diagonalen eines Rechtecks
In einem Rechteck sind die Diagonalen gleich lang, wie unten gezeigt wird. Die Argumentation ist wie folgt; Ein Rechteck ist ein Parallelogramm mit allen rechten Winkeln und erbt daher alle Eigenschaften des Parallelogramms, einschließlich der Formel, die die Länge der Diagonalen angibt:
F.zwei = azwei+ dzwei + 2 a d Cos (α)
Gzwei = azwei + dzwei - 2 und Cos (α)
mit α = 90º
Was Cos (90º) = 0, dann passiert es, dass:
F.zwei = gzwei = azwei + dzwei
Das ist f = g, und damit die Längen F. Y. G der beiden Diagonalen des Rechtecks sind gleich und ihre Länge ist gegeben durch:
Diagonale Länge eines Rechtecks = √ (azwei + bzwei)
Auch wenn in einem Rechteck mit angrenzenden Seiten zu Y. b Eine Seite wird als Basis genommen, die andere Seite ist die Höhe und folglich ist die Fläche des Rechtecks:
Fläche des Rechtecks = a x b.
Der Umfang ist die Summe aller Seiten des Rechtecks, aber da die Gegensätze gleich sind, folgt dies für ein Rechteck mit Seiten zu Y. b Der Umfang wird durch die folgende Formel angegeben:
Umfang des Rechtecks = 2 (a + b)
Quadrat
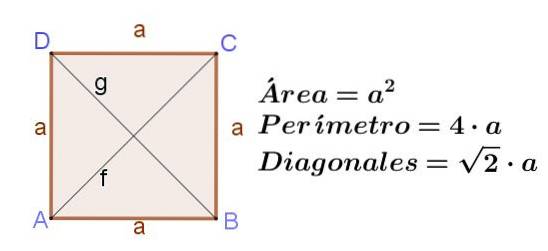
Das Quadrat ist ein Rechteck, dessen benachbarte Seiten gleich lang sind. Wenn das Quadrat eine Seite hat zu, dann seine Diagonalen F. Y. G haben die gleiche Länge, die ist f = g = (√2) a.
Die Fläche eines Quadrats ist seine Seite im Quadrat:
Fläche eines Quadrats = azwei
Der Umfang eines Quadrats ist doppelt so groß wie die Seite:
Umfang eines Quadrats = 4 a
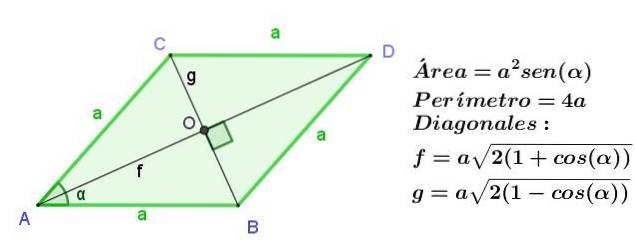
Diamant
Die Raute ist ein Parallelogramm, dessen benachbarte Seiten gleich lang sind, aber wie bei einem Parallelogramm sind die gegenüberliegenden Seiten dann gleich, Alle Seiten einer Raute sind gleich lang.
Die Diagonalen einer Raute sind unterschiedlich lang, schneiden sich aber rechtwinklig.
Beispiele
Beispiel 1
Zeigen Sie, dass sich in einem Viereck (nicht gekreuzt) die Innenwinkel zu 360 ° addieren.
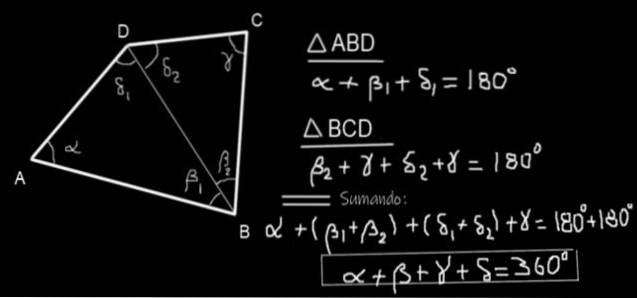
Ein viereckiges ABCD wird betrachtet (siehe 10) und die Diagonale BD wird gezeichnet. Es werden zwei Dreiecke ABD und BCD gebildet. Die Summe der Innenwinkel des Dreiecks ABD ist:
α + β1 + δ1 = 180º
Und die Summe der Innenwinkel des Dreiecks BCD ist:
β2 + γ + δzwei = 180º
Addieren wir die beiden Gleichungen, die wir erhalten:
α + β1 + δ1 + βzwei + γ + δzwei = 180º + 180º
Gruppierung:
α + (β1 + βzwei) + (δ1 + δzwei) + γ = 2 * 180º
Durch Gruppieren und Umbenennen wird schließlich gezeigt, dass:
α + β + δ + γ = 360º
Beispiel 2
Zeigen Sie, dass der Median eines Trapezes parallel zu seinen Basen ist und seine Länge die Halbwertsumme der Basen ist.
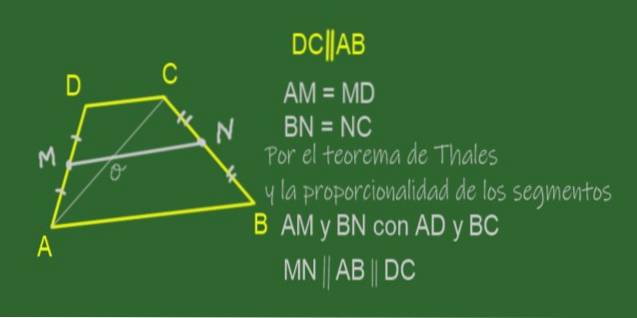
Der Median eines Trapezes ist das Segment, das die Mittelpunkte seiner Seiten, dh die nicht parallelen Seiten, verbindet. In dem in Abbildung 11 gezeigten Trapez ABCD ist der Median MN.
Da M der Mittelpunkt von AD und N der Mittelpunkt von BC ist, ist es wahr, dass die AM / AD- und BN / BC-Verhältnisse gleich sind.
Das heißt, AM ist proportional zu BN in demselben Verhältnis wie AD zu BC, daher sind die Bedingungen für die Anwendung des (reziproken) Theorems von Thales gegeben, der Folgendes besagt:
""Wenn proportionale Segmente in drei oder mehr Linien bestimmt werden, die von zwei Sekanten geschnitten werden, sind diese Linien alle parallel"".
In unserem Fall wird der Schluss gezogen, dass die Leitungen MN, AB und DC parallel zueinander sind, daher:
"L.Der Median eines Trapezes verläuft parallel zu seinen Basen"".
Nun wird der Thales-Satz angewendet:
""Eine Reihe von Parallelen, die von zwei oder mehr Sekanten geschnitten werden, bestimmen proportionale Segmente"".
In unserem Fall ist AD = 2 AM, AC = 2 AO, so dass das Dreieck DAC dem Dreieck MAO ähnlich ist und folglich DC = 2 MO.
Ein ähnliches Argument erlaubt es uns zu bestätigen, dass CAB CON ähnlich ist, wobei CA = 2 CO und CB = 2 CN. Daraus folgt sofort, dass AB = 2 ON ist.
Kurz gesagt, AB = 2 ON und DC = 2 MO. Wenn wir also hinzufügen, haben wir:
AB + DC = 2 EIN + 2 MO = 2 (MO + EIN) = 2 MN
Schließlich wird MN gelöscht:
MN = (AB + DC) / 2
Und es wird geschlossen, dass der Median eines Trapezes die Halbsumme der Basen misst, oder mit anderen Worten: Der Median misst die Summe der Basen, geteilt durch zwei.
Beispiel 3
Zeigen Sie, dass sich in einer Raute die Diagonalen rechtwinklig schneiden.

Die Tafel in Abbildung 12 zeigt den notwendigen Aufbau. Zuerst wird das Parallelogramm ABCD mit AB = BC, dh einer Raute, gezeichnet. Die Diagonalen AC und DB bestimmen acht in der Abbildung gezeigte Winkel.
Unter Verwendung des Satzes (a.i.p.), der besagt, dass abwechselnde Innenwinkel zwischen Parallelen, die durch eine Sekante geschnitten werden, gleiche Winkel bestimmen, können wir Folgendes feststellen:
α1 = γ1, α2 = γ2, δ1 = Β1 und δ2 = β2. (*)
Da andererseits die benachbarten Seiten einer Raute gleich lang sind, werden vier gleichschenklige Dreiecke bestimmt:
DAB, BCD, CDA und ABC
Nun wird der Dreieckssatz (gleichschenklig) aufgerufen, der besagt, dass die an die Basis angrenzenden Winkel gleich groß sind, woraus geschlossen wird, dass:
δ1 = β2, δ2 = β1, α2 = γ1 und α1 = γ2 (**)
Wenn die Beziehungen (*) und (**) kombiniert werden, wird die folgende Winkelgleichheit erreicht:
α1 = α2 = γ1 = γ1 einerseits und β1 = Β2 = δ1 = δ2 auf der anderen Seite.
Wenn wir uns an den Satz der gleichen Dreiecke erinnern, der besagt, dass zwei Dreiecke mit einer gleichen Seite zwischen zwei gleichen Winkeln gleich sind, haben wir:
AOD = AOB und folglich auch die Winkel ∡AOD = ∡AOB.
Dann ist ∡AOD + ∡AOB = 180º, aber da beide Winkel gleich groß sind, haben wir 2 ∡AOD = 180º, was impliziert, dass ∡AOD = 90º ist.
Das heißt, es wird geometrisch gezeigt, dass sich die Diagonalen einer Raute rechtwinklig schneiden.
Übungen gelöst
- Übung 1
Zeigen Sie, dass in einem rechten Trapez die nicht rechten Winkel komplementär sind.
Lösung
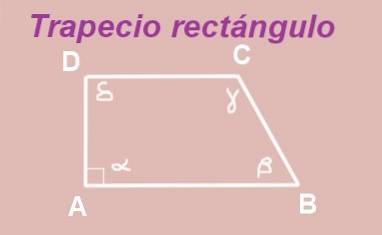
Das Trapez ABCD ist mit parallelen Basen AB und DC aufgebaut. Der Innenwinkel von Scheitelpunkt A ist richtig (er misst 90º), also haben wir ein rechtes Trapez.
Die Winkel α und δ sind Innenwinkel zwischen zwei Parallelen AB und DC, daher sind sie gleich, dh δ = α = 90º.
Andererseits wurde gezeigt, dass sich die Summe der Innenwinkel eines Vierecks zu 360º summiert, dh:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Das Obige führt zu:
β + δ = 180º
Bestätigung, was zeigen wollte, dass die Winkel β und δ komplementär sind.
- Übung 2
Ein Parallelogramm ABCD hat AB = 2 cm und AD = 1 cm, zusätzlich beträgt der Winkel BAD 30º. Bestimmen Sie die Fläche des Parallelogramms und die Länge seiner beiden Diagonalen.
Lösung
Die Fläche eines Parallelogramms ist das Produkt aus der Länge seiner Basis multipliziert mit seiner Höhe. In diesem Fall wird die Länge des Segments b = AB = 2 cm zugrunde gelegt, die andere Seite hat die Länge a = AD = 1 cm und die Höhe h wird wie folgt berechnet:
h = AD * Sen (30º) = 1 cm * (1/2) = ½ cm.
Also: Fläche = b * h = 2 cm * ½ cm = 1 cmzwei.
Verweise
- C. E. A. (2003). Elemente der Geometrie: mit Übungen und Geometrie des Kompasses. Universität von Medellin.
- Campos, F., Cerecedo, F. J. (2014). Mathematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Entdecken Sie Polygone. Benchmark Education Company.
- Hendrik, V. (2013). Verallgemeinerte Polygone. Birkhäuser.
- IGER. (s.f.). Mathematik Erstes Semester Tacaná. IGER.
- Jr. Geometrie. (2014). Polygone. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematik: Argumentation und Anwendungen (Zehnte Ausgabe). Pearson Ausbildung.
- Patiño, M. (2006). Mathematik 5. Editorial Progreso.
- Wikipedia. Vierecke. Wiederhergestellt von: es.wikipedia.com


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.