
Beispiele für sphärische Koordinaten und gelöste Übungen

Das sphärische Koordinaten sind ein Punktortungssystem im dreidimensionalen Raum, das aus einer Radialkoordinate und zwei Winkelkoordinaten besteht, die als Polarkoordinate und Azimutkoordinate bezeichnet werden.
Abbildung 1, die wir unten sehen, zeigt die sphärischen Koordinaten (r, θ, φ) eines Punktes M. Diese Koordinaten beziehen sich auf ein orthogonales System der kartesischen Achsen X, Y, Z des Ursprungs O..
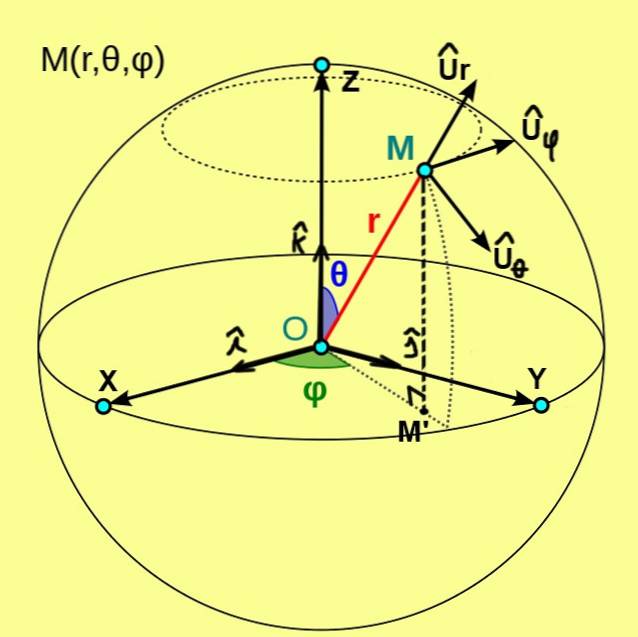
In diesem Fall ist die Koordinate r des Punktes M der Abstand von diesem Punkt zum Ursprung O. Die Polarkoordinate θ repräsentiert den Winkel zwischen der positiven Halbachse Z und dem Radiusvektor OM. Während die Azimutkoordinate φ der Winkel zwischen der positiven Halbachse X und dem Radiusvektor OM 'ist, ist M' die orthogonale Projektion von M auf die XY-Ebene.
Die Radialkoordinate r nimmt nur positive Werte an, aber wenn sich ein Punkt am Ursprung befindet, ist r = 0. Die Polarkoordinate θ nimmt als Minimalwert 0º für Punkte auf der positiven Z-Halbachse und ein Maximalwert 180º für die Punkte auf der negativen Z-Halbachse an. Schließlich nimmt die Azimutkoordinate φ als Minimalwert 0º an und eine maximale Höhe von 360º.
0 ≤ r < ∞
0 ≤ θ ≤ 180º
0 ≤ φ < 360º
Artikelverzeichnis
- 1 Änderung der Koordinaten
- 1.1 Vektorbasis in sphärischen Koordinaten
- 1.2 Linien- und Volumenelemente in sphärischen Koordinaten
- 2 Beziehung zu geografischen Koordinaten
- 2.1 Formeln zum Ändern von geografisch zu sphärisch
- 3 Beispiele
- 3.1 Beispiel 1
- 3.2 Beispiel 2
- 4 Übungen
- 4.1 Übung 1
- 4.2 Übung 2
- 5 Referenzen
Änderung der Koordinaten
Die Formeln, die es ermöglichen, die kartesischen Koordinaten (x, y, z) eines Punktes M zu erhalten, werden unten angegeben, vorausgesetzt, die sphärischen Koordinaten desselben (r, θ, φ) Punkts sind bekannt:
x = r Sen (θ) Cos (φ)
y = r Sen (θ) Sen (φ)
z = r Cos (θ)
Auf die gleiche Weise ist es nützlich, die Beziehungen zu finden, die von den kartesischen Koordinaten (x, y, z) eines gegebenen Punktes zu den sphärischen Koordinaten dieses Punktes gehen:
r = √ (x ^ 2 + y ^ 2 + z ^ 2)
θ = Arctan (√ (x ^ 2 + y ^ 2) / z)
φ = Arctan (y / x)
Vektorbasis in sphärischen Koordinaten
Aus den sphärischen Koordinaten wird eine orthonormale Basis von Basisvektoren definiert, die mit bezeichnet sind Ur, Uθ, Uφ. Abbildung 1 zeigt diese drei Einheitsvektoren mit den folgenden Eigenschaften:
- Ur ist der Einheitsvektor, der die radiale Linie θ = ctte und φ = ctte tangiert;
- Uθ ist der Einheitsvektor, der den Bogen φ = ctte und r = ctte tangiert;
- Uφ ist der Einheitsvektor, der den Bogen r = ctte und θ = ctte tangiert.
Linien- und Volumenelemente in sphärischen Koordinaten
Der Positionsvektor eines Raumpunktes in sphärischen Koordinaten lautet wie folgt:
r = r Ur
Eine infinitesimale Variation oder Verschiebung eines Punktes im dreidimensionalen Raum in diesen Koordinaten wird jedoch durch die folgende Vektorbeziehung ausgedrückt:
dr = dr Ur + r dθ Uθ + r Sen (θ) dφ Uφ
Schließlich wird ein infinitesimales Volumen dV in sphärischen Koordinaten wie folgt geschrieben:
dV = r ^ 2 Sen (θ) dr dθ dφ
Diese Beziehungen sind sehr nützlich für die Berechnung von Linien- und Volumenintegralen in physikalischen Situationen mit sphärischer Symmetrie..
Beziehung zu geografischen Koordinaten
Unter geografischen Koordinaten werden solche verstanden, die dazu dienen, Orte auf der Erdoberfläche zu lokalisieren. Dieses System verwendet die Koordinaten von Breite und Länge, um die Position auf der Erdoberfläche zu lokalisieren..
Im geografischen Koordinatensystem wird angenommen, dass die Erdoberfläche mit dem Radius Rt sphärisch ist, obwohl bekannt ist, dass sie an den Polen abgeflacht ist, und eine Reihe von imaginären Linien, die als Parallelen und Meridiane bezeichnet werden, wird berücksichtigt.
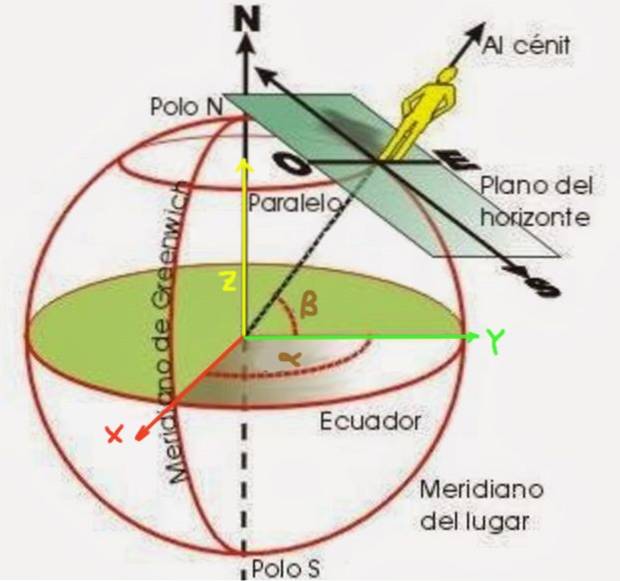
Der Breitengrad β ist ein Winkel, der durch einen Radius gebildet wird, der vom Erdmittelpunkt bis zu dem Punkt beginnt, den Sie positionieren möchten. Sie wird von der Äquatorialebene aus gemessen, wie in Abbildung 2 dargestellt. Andererseits ist der Längengrad α der Winkel, den der Meridian des zu lokalisierenden Punkts in Bezug auf den Nullmeridian (bekannt als Greenwich-Meridian) bildet..
Der Breitengrad kann der nördliche oder südliche Breitengrad sein, je nachdem, ob sich der Ort, den Sie lokalisieren, auf der Nordhalbkugel oder auf der Südhalbkugel befindet. In ähnlicher Weise kann der Längengrad westlich oder östlich sein, je nachdem, ob der Standort westlich oder östlich des Nullmeridians liegt..
Formeln zum Ändern von geografisch zu sphärisch
Um diese Formeln zu erhalten, muss zunächst ein Koordinatensystem erstellt werden. Die XY-Ebene wird so gewählt, dass sie mit der Äquatorialebene zusammenfällt, wobei die positive X-Halbachse diejenige ist, die vom Erdmittelpunkt verläuft und durch den Nullmeridian verläuft. Die Y-Achse verläuft wiederum durch den 90 ° E-Meridian. Die Erdoberfläche hat einen Radius Rt.
Mit diesem Koordinatensystem sehen die Transformationen von geografisch zu sphärisch folgendermaßen aus:
αEβN → (Rt, θ = 90º-β, φ = α)
αOβN → (Rt, θ = 90º-β, φ = 360º-α)
αEβS → (Rt, θ = 90º + β, φ = α)
αOβS → (Rt, θ = 90º + β, φ = 360º-α)
Beispiele
Beispiel 1
Die geografischen Koordinaten von Palma de Mallorca (Spanien) sind:
East Longitude 38.847º und North Latitude 39.570º. Um die Kugelkoordinaten zu bestimmen, die Palma de Mallorca entsprechen, wird die erste der Formeln der Formeln im vorherigen Abschnitt angewendet:
38.847ºE39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)
Die sphärischen Koordinaten sind also:
Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)
In der vorherigen Antwort haben wir r gleich dem durchschnittlichen Radius der Erde genommen.
Beispiel 2
Wenn Sie wissen, dass die Falklandinseln (Malvinas) geografische Koordinaten von 59ºO 51,75ºS haben, bestimmen Sie die entsprechenden Polarkoordinaten. Denken Sie daran, dass die X-Achse vom Erdmittelpunkt zum 0º-Meridian und auf der Äquatorialebene verläuft. die Y-Achse auch in der Äquatorialebene und durch den 90º-Westmeridian verlaufend; schließlich die Z-Achse auf der Erdrotationsachse in Süd-Nord-Richtung.
Um dann die entsprechenden Kugelkoordinaten zu finden, verwenden wir die im vorherigen Abschnitt dargestellten Formeln:
59ºO 51,75ºS → (r = 6371 km, θ = 90º + 51,75º, φ = 360º-59º) das heißt
Falklandinseln: (r = 6371 km, θ = 141,75º, φ = 301º)
Ausbildung
Übung 1
Finden Sie die kartesischen Koordinaten von Palma de Mallorca im kartesischen XYZ-Referenzsystem (siehe Abbildung 2).
Lösung: Zuvor wurden in Beispiel 1 die sphärischen Koordinaten ausgehend von den geografischen Koordinaten von Palma de Mallorca erhalten. Die oben dargestellten Formeln können also verwendet werden, um von sphärisch zu kartesisch zu wechseln:
x = 6371 km Sen (50,43º) Cos (38,85º)
y = 6371 km Sen (50,43º) Sen (38,85º)
z = 6371 km Cos (50,43º)
Durchführen der entsprechenden Berechnungen haben wir:
Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)
Übung 2
Finden Sie die kartesischen Koordinaten der Falklandinseln im kartesischen XYZ-Referenzsystem (siehe Abbildung 2).
Lösung: Zuvor wurden in Beispiel 2 die sphärischen Koordinaten ausgehend von den geografischen Koordinaten der Falklandinseln erhalten. Die oben dargestellten Formeln können also verwendet werden, um von sphärisch zu kartesisch zu wechseln:
x = 6371 km Sen (141,75 °) Cos (301 °)
y = 6371 km Sen (141,75º) Sen (301º)
z = 6371 km Cos (141,75º)
Durch Ausführen der entsprechenden Berechnungen erhalten wir:
Falklandinseln: (x = 2031 km, y = -3381 km, z = -5003)
Verweise
- Arfken G und Weber H. (2012). Mathematische Methoden für Physiker. Eine umfassende Anleitung. 7. Auflage. Akademische Presse. ISBN 978-0-12-384654-9
- Berechnung cc. Gelöste Probleme mit Zylinder- und Kugelkoordinaten. Wiederhergestellt von: calculo.cc
- Astronomie-Workshop. Breiten-und Längengrad. Wiederhergestellt von: tarifamates.blogspot.com/
- Weisstein, Eric W. "Sphärische Koordinaten." Aus MathWorld-A Wolfram Web. Wiederhergestellt von: mathworld.wolfram.com
- Wikipedia. Sphärisches Koordinatensystem. Wiederhergestellt von: en.wikipedia.com
- Wikipedia. Vektorfelder in Zylinder- und Kugelkoordinaten. Wiederhergestellt von: en.wikipedia.com

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.