Das Boltzmann-Konstante ist der Wert, der die durchschnittliche kinetische Energie eines thermodynamischen Systems oder eines Objekts mit seiner absoluten Temperatur in Beziehung setzt. Obwohl sie oft verwechselt werden, sind Temperatur und Energie nicht dasselbe Konzept.
Die Temperatur ist ein Maß für die Energie, aber nicht die Energie selbst. Mit der Boltzmannschen Konstante sind sie folgendermaßen miteinander verbunden:
UNDc = (3/2) kB. T.
Diese Gleichung gilt für ein einatomiges ideales Gasmolekül mit Masse m, wo UNDc ist seine kinetische Energie in Joules, kB. ist Boltzmanns Konstante und T. ist die absolute Temperatur in Kelvin.
Auf diese Weise steigt mit steigender Temperatur auch die durchschnittliche kinetische Energie pro Substanzmolekül an, wie dies zu erwarten ist. Und das Gegenteil passiert, wenn die Temperatur abnimmt und der Punkt erreicht wird, an dem, wenn alle Bewegungen aufhören, die niedrigstmögliche Temperatur oder der absolute Nullpunkt erreicht wird..
Wenn man von durchschnittlicher kinetischer Energie spricht, muss man bedenken, dass kinetische Energie mit Bewegung verbunden ist. Und Partikel können sich auf viele Arten bewegen, z. B. durch Bewegen, Drehen oder Vibrieren. Natürlich werden es nicht alle auf die gleiche Weise tun, und da sie unzählig sind, wird der Durchschnitt zur Charakterisierung des Systems herangezogen..
Einige Energiezustände sind wahrscheinlicher als andere. Dieses Konzept ist in der Thermodynamik von radikaler Bedeutung. Die in der obigen Gleichung berücksichtigte Energie ist translatorische kinetische Energie. Die Wahrscheinlichkeit von Zuständen und ihre Beziehung zur Boltzmannschen Konstante wird etwas später diskutiert..
2018 wurde der Kelvin neu definiert und damit die Boltzmann-Konstante, die im internationalen System ungefähr 1,380649 x 10 beträgt-2. 3 J. K.-1. Für die Boltzmann-Konstante, die in zahlreichen Labors auf der ganzen Welt mit verschiedenen Methoden bestimmt wurde, kann viel mehr Präzision erreicht werden..
Artikelverzeichnis
Die berühmte Konstante verdankt ihren Namen dem in Wien geborenen Physiker Ludwig Boltzmann (1844-1906), der sein Leben als Wissenschaftler der Untersuchung des statistischen Verhaltens von Systemen mit vielen Teilchen aus Sicht der Newtonschen Mechanik widmete..
Obwohl heute die Existenz des Atoms allgemein anerkannt ist, wurde im neunzehnten Jahrhundert der Glaube, ob das Atom wirklich existierte oder ein Kunstgriff war, mit dem viele physikalische Phänomene erklärt wurden, in voller Debatte diskutiert..
Boltzmann war ein überzeugter Verfechter der Existenz des Atoms und wurde zu seiner Zeit von vielen Kollegen scharf kritisiert, die der Ansicht waren, dass es unlösbare Paradoxien enthielt..
Er erklärte, dass beobachtbare Phänomene auf makroskopischer Ebene durch die statistischen Eigenschaften von Teilchen wie Atomen und Molekülen erklärt werden könnten..
Vielleicht war diese Kritik auf die tiefgreifende Depression zurückzuführen, die ihn Anfang September 1906 dazu brachte, sich das Leben zu nehmen, als er noch viel zu tun hatte, da er als einer der großen theoretischen Physiker seiner Zeit galt und es gab Es bleibt nur noch sehr wenig übrig, was andere Wissenschaftler dazu beitragen, die Richtigkeit ihrer Theorien zu bestätigen.
Es dauerte nicht lange nach seinem Tod, bis sich neue Entdeckungen über die Natur des Atoms und seiner Partikelbestandteile summierten, um Boltzmann Recht zu geben..
Nun die Boltzmann-Konstante kB. es wurde eingeführt, wie es heute einige Zeit nach den Arbeiten des österreichischen Physikers bekannt ist. Es war Max Planck, in seinem Gesetz über die Emission des schwarzen Körpers, ein Werk, das er 1901 vorstellte und das ihm damals den Wert 1,34 x 10 gab−23 J / K..
Um 1933 wurde Boltzmanns Grabstein in Wien als posthume Hommage eine Gedenktafel mit der Definition der Entropie der berühmten Konstante hinzugefügt: S = kB. log W., Gleichung, die später diskutiert wird.
Heute ist die Boltzmann-Konstante für die Anwendung der Gesetze der Thermodynamik, der statistischen Mechanik und der Informationstheorie unverzichtbar, deren Pionier dieser traurige Physiker war..
Gase können sowohl makroskopisch als auch mikroskopisch beschrieben werden. Für die Erstbeschreibung gibt es Konzepte wie Dichte, Temperatur und Druck.
Es sollte jedoch beachtet werden, dass ein Gas aus vielen Partikeln besteht, die eine globale Tendenz zu einem bestimmten Verhalten haben. Dieser Trend wird makroskopisch gemessen. Eine Möglichkeit zur Bestimmung der Boltzmann-Konstante ist die bekannte ideale Gasgleichung:
p.V = n. R. T.
Hier p ist der Gasdruck, V. ist sein Volumen, n ist die Anzahl der vorhandenen Mol, R. ist die Gaskonstante und T. ist die Temperatur. In einem Mol idealem Gas ist die folgende Beziehung zwischen dem Produkt erfüllt p.V., und die translatorische kinetische Energie K. Das ganze Set ist:
p.V = (2/3). K.
Daher ist die kinetische Energie:
K = (3/2) n.R.T.
Durch Division durch die Gesamtzahl der vorhandenen Moleküle, die als N bezeichnet wird, wird die durchschnittliche kinetische Energie eines einzelnen Partikels erhalten:
UNDc = K / N.
UNDc= (3 / 2N) n.R.T.
In einem Mol gibt es die Anzahl der Partikel N von AvogadroZU, und daher ist die Gesamtzahl der Teilchen N. = nNA, verbleibend:
UNDc = (3 / 2nNZU) n.R.T.
Genau der Quotient R / N.ZU ist die Boltzmannsche Konstante, wodurch gezeigt wird, dass die durchschnittliche kinetische Translationsenergie eines Teilchens nur von der absoluten Temperatur T und nicht von anderen Größen wie Druck, Volumen oder sogar der Art des Moleküls abhängt:
UNDc = (3/2) kB.. T.
Ein Gas hat eine bestimmte Temperatur, aber diese Temperatur kann verschiedenen Zuständen innerer Energie entsprechen. Wie man diesen Unterschied visualisiert?
Betrachten Sie den gleichzeitigen Wurf von 4 Münzen und die Art und Weise, wie sie fallen können:
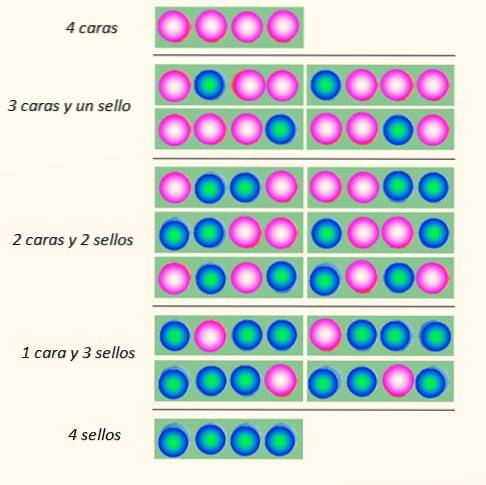
Der Münzsatz kann insgesamt 5 Zustände annehmen, die berücksichtigt werden makroskopisch, in der Abbildung beschrieben. Welcher dieser Zustände der Leser sagen würde, ist der wahrscheinlichste?
Die Antwort sollte der Zustand von 2 Köpfen und 2 Schwänzen sein, da Sie insgesamt 6 Möglichkeiten haben, von den 16 in der Abbildung dargestellten. Und 24 = 16. Diese entsprechen den Zuständen mikroskopisch.
Was ist, wenn 20 statt 4 Münzen geworfen werden? Es würde insgesamt 2 gebenzwanzig Möglichkeiten oder "mikroskopische Zustände". Es ist eine viel größere Anzahl und schwieriger zu handhaben. Um die Handhabung großer Zahlen zu erleichtern, sind Logarithmen sehr geeignet.
Nun scheint es offensichtlich zu sein, dass der Staat mit der größten Störung am wahrscheinlichsten ist. Mehr geordnete Zustände wie 4 Köpfe oder 4 Siegel sind etwas weniger wahrscheinlich.
Die Entropie eines makroskopischen Zustands S ist definiert als:
S = kB. ln w
Wo w ist die Anzahl der möglichen mikroskopischen Zustände des Systems und kB. ist Boltzmanns Konstante. Was ln w ist dimensionslos, Entropie hat die gleichen Einheiten wie kB.: Joule / K..
Dies ist die berühmte Gleichung auf Boltzmanns Grabstein in Wien. Relevant ist jedoch nicht nur die Entropie, sondern auch ihre Veränderung:
ΔS = kB. ln wzwei - kB. ln w1 = kB. ln (wzwei/ w1)
Der Wert der Boltzmannschen Konstante wird experimentell mit äußerster Präzision mit Messungen basierend auf erhalten akustische Thermometrie, die unter Verwendung der Eigenschaft durchgeführt werden, die die Abhängigkeit der Schallgeschwindigkeit in einem Gas von seiner Temperatur festlegt.
In der Tat ist die Schallgeschwindigkeit in einem Gas gegeben durch:
B.adiabatisch = γp
Und ρ ist die Dichte des Gases. Für die obige Gleichung, p ist der Druck des betreffenden Gases und γ ist der adiabatische Koeffizient, dessen Wert für ein bestimmtes Gas in Tabellen angegeben ist.
Metrologie-Institute experimentieren auch mit anderen Methoden zur Messung der Konstante, wie z Johnson-Rauschthermometrie, Dabei werden thermische Schwankungen verwendet, die in Materialien, insbesondere in Leitern, zufällig auftreten.
Finden:
a) Durchschnittliche translatorische kinetische Energie UNDc welches ein ideales Gasmolekül bei 25 ºC hat
b) Translationale kinetische Energie K. der Moleküle in 1 Mol dieses Gases
c) Die durchschnittliche Geschwindigkeit eines Sauerstoffmoleküls bei 25 ºC
mSauerstoff = 16 x 10 -3 kg / mol
zu) UNDc = (3/2) k T = 1,5 x 1,380649 x 10-2. 3J. K.-1 x 298 K = 6,2 x 10-einundzwanzig J.
b) K = (3/2) n.R.T = 5 · 1 Mol · 8,314 J / Mol K · 298 K = 3716 J.
c) UNDc = ½ mvzwei, Unter Berücksichtigung, dass das Sauerstoffmolekül zweiatomig ist und die Molmasse mit 2 multipliziert werden muss, haben wir:
Finden Sie die Entropieänderung, wenn 1 Mol Gas ein Volumen von 0,5 m einnimmt3 dehnt sich auf 1 m aus3.
ΔS = kB. ln (wzwei/ w1)
wzwei= 2N.w1 (Es gab 24 mikroskopische Zustände für den Wurf der 4 Münzen, erinnerst du dich?)
Wobei N die Anzahl der in 0,5 Mol Gas vorhandenen Partikel 0,5 x N istZU::
ΔS = kB. ln (2N. w1/ w1) = kB. ln 2N.= kB. 0,5 N.ZU In 2 = 2,88 J / K.
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.