Sofortige Beschleunigung, was es ist, wie es berechnet wird und trainiert

Das sofortige Beschleunigung Es ist die Änderung, die die Geschwindigkeit pro Zeiteinheit zu jedem Zeitpunkt der Bewegung erfährt. Genau zu dem Zeitpunkt, als die „Dragster”Von dem fotografierten Bild trug es eine Beschleunigung von 29,4 m / s^zwei. Dies bedeutet, dass zu diesem Zeitpunkt seine Geschwindigkeit innerhalb von 1 s um 29,4 m / s erhöht wurde. Dies entspricht 105 km / h in nur 1 Sekunde.

Ein Dragster-Wettbewerb lässt sich leicht modellieren, vorausgesetzt, der Rennwagen ist ein Punktobjekt. P. das bewegt sich in einer geraden Linie. Auf dieser Linie wird eine mit Ursprung ausgerichtete Achse gewählt ODER dass wir die Achse nennen werdenOCHSE) oder nur Achse x.

Die kinematischen Variablen, die die Bewegung definieren und beschreiben, sind:

• Die Position x
• Verschiebung Δx
• Geschwindigkeit v
• Beschleunigung zu

Sie sind alle Vektorgrößen. Deshalb haben sie eine Größe, eine Richtung und einen Sinn.

Bei geradliniger Bewegung gibt es nur zwei mögliche Richtungen: positiv (+) in Richtung (OCHSE) oder negativ (-) in entgegengesetzter Richtung von (OCHSE). Daher ist es möglich, auf die formale Vektornotation zu verzichten und die Zeichen zu verwenden, um den Sinn der Größe anzuzeigen.

Artikelverzeichnis

• 1 Wie wird die Beschleunigung berechnet??
• 2 Geschwindigkeit durch sofortige Beschleunigung
• 3 Gelöste Übungen
  • 3.1 Übung 1
  • 3.2 Übung 2
  • 3.3 Übung 3
  • 3.4 Übung 4
• 4 Referenzen

Wie berechnet man die Beschleunigung??

Angenommen, das im Moment t Das Teilchen hat Geschwindigkeit v (t) und im Augenblick t ' seine Geschwindigkeit ist v (t ').

Die Änderung, die die Geschwindigkeit in diesem Zeitraum hatte, war also Δv = v (t ') - v (t). Daher die Beschleunigung im Zeitraffer Δt = t '- t , würde durch den Quotienten gegeben sein:

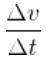
Dieser Quotient ist die durchschnittliche Beschleunigung bei_m in der Zeitspanne Δt zwischen den Zeitpunkten t und t '.

Wenn wir die Beschleunigung gerade zum Zeitpunkt t berechnen wollten, sollte t 'eine unwesentlich größere Größe als t sein. Damit sollte Δt, das die Differenz zwischen den beiden ist, nahezu Null sein.

Mathematisch wird es wie folgt angegeben: Δt → 0 und es wird erhalten:

ICH) Ein Teilchen bewegt sich mit konstanter Geschwindigkeit v entlang der X-Achse₀ = 3 m / s. Was wird die Beschleunigung des Teilchens sein?

Die Ableitung einer Konstanten ist Null, daher ist die Beschleunigung eines Teilchens, das sich mit konstanter Geschwindigkeit bewegt, Null.

II) Ein Teilchen bewegt sich auf der Achse x und seine Geschwindigkeit ändert sich mit der Zeit gemäß der folgenden Formel:

v (t) = 2 - 3t

Wobei die Geschwindigkeit in m / s und die Zeit in s gemessen wird. Was wird die Beschleunigung des Teilchens sein?

Das Ergebnis wird folgendermaßen interpretiert: Für jeden Moment beträgt die Beschleunigung -3 m / s.

Zwischen den Zeitpunkten 0 s und 2/3 s ist die Geschwindigkeit positiv, während die Beschleunigung negativ ist, dh in diesem Intervall verringert das Teilchen seine Geschwindigkeit oder verlangsamt sich.

Im Moment 2/3 s wird seine Geschwindigkeit Null, aber wenn eine Beschleunigung von -3 m / s verbleibt, kehrt sich die Geschwindigkeit ab diesem Moment um (sie wird negativ)..

In den Augenblicken nach ⅔ s beschleunigt sich das Teilchen, da jedes Mal, wenn seine Geschwindigkeit negativer wird, dh seine Geschwindigkeit (Geschwindigkeitsmodul) wächst.

III) Die Abbildung zeigt eine Kurve, die die Geschwindigkeit als Funktion der Zeit für ein Teilchen darstellt, das sich entlang der X-Achse bewegt. Ermitteln Sie das Vorzeichen der Beschleunigung zu den Zeitpunkten t₁, t_zwei und du₃. Geben Sie auch an, ob das Partikel beschleunigt oder verlangsamt.

Die Beschleunigung ist die Ableitung der Geschwindigkeitsfunktion, daher entspricht sie der Steigung der Tangentenlinie zur Kurve v (t) für einen gegebenen Zeitpunkt t.

Für den Moment t₁, Die Steigung ist negativ, daher ist die Beschleunigung negativ. Und da in diesem Moment die Geschwindigkeit positiv ist, können wir bestätigen, dass sich das Teilchen in diesem Moment verlangsamt.

Für den Moment t_zwei Die Tangentenlinie zur Kurve v (t) ist horizontal, daher ist ihre Steigung Null. Das Mobiltelefon hat keine Beschleunigung, daher bei t_zwei Das Teilchen beschleunigt oder bremst weder ab.

Für den Moment t₃, Die Steigung der Tangentenlinie zur Kurve v (t) ist positiv. Bei einer positiven Beschleunigung beschleunigt das Teilchen wirklich, weil in diesem Moment auch die Geschwindigkeit positiv ist.

Geschwindigkeit durch sofortige Beschleunigung

Im vorherigen Abschnitt wurde die momentane Beschleunigung aus der momentanen Geschwindigkeit definiert. Mit anderen Worten, wenn die Geschwindigkeit zu jedem Zeitpunkt bekannt ist, ist es auch möglich, die Beschleunigung zu jedem Zeitpunkt der Bewegung zu kennen..

Der umgekehrte Vorgang ist möglich. Das heißt, wenn die Beschleunigung für jeden Moment bekannt ist, kann die momentane Geschwindigkeit berechnet werden.

Wenn die Operation, die den Übergang von der Geschwindigkeit zur Beschleunigung ermöglicht, die Ableitung ist, ist die entgegengesetzte mathematische Operation die Integration.  

Gelöste Übungen

Übung 1

Die Beschleunigung eines Teilchens, das sich entlang der X-Achse bewegt, beträgt a (t) = ¼ t^zwei. Wobei t in Sekunden und a in m / s gemessen wird. Bestimmen Sie die Beschleunigung und Geschwindigkeit des Partikels bei 2 s Bewegung, wobei Sie wissen, dass zum Anfangszeitpunkt t₀ = 0 war in Ruhe.

Antworten

Bei 2 s beträgt die Beschleunigung 1 m / s^zwei und die Geschwindigkeit für den Moment t wird gegeben durch:

Übung 2

Ein Objekt bewegt sich entlang der X-Achse mit einer Geschwindigkeit in m / s, gegeben durch:

v (t) = 3 t^zwei - 2 t, wobei t in Sekunden gemessen wird. Bestimmen Sie die Beschleunigung zu Zeiten: 0s, 1s, 3s.

Antworten

Unter Verwendung der Ableitung von v (t) in Bezug auf t wird die Beschleunigung zu jedem Zeitpunkt erhalten:

a (t) = 6t -2

Dann ist a (0) = -2 m / s^zwei ;; a (1) = 4 m / s^zwei ;; a (3) = 16 m / s^zwei .

Übung 3

Eine Metallkugel wird von der Oberseite eines Gebäudes freigegeben. Die fallende Beschleunigung ist die Erdbeschleunigung, die durch den Wert 10 m / s2 angenähert werden kann und nach unten zeigt. Bestimmen Sie die Geschwindigkeit der Kugel 3 s nach dem Loslassen.

Antworten

Dieses Problem beinhaltet die Beschleunigung der Schwerkraft. Die vertikale Richtung als positiv nehmen Nieder, Wir haben, dass die Beschleunigung der Kugel ist:

a (t) = 10 m / s^zwei 

Und die Geschwindigkeit wird gegeben durch: 

Übung 4

Eine Metallkugel wird mit einer Anfangsgeschwindigkeit von 30 m / s nach oben geschossen. Die Bewegungsbeschleunigung ist die Erdbeschleunigung, die durch den Wert 10 m / s angenähert werden kann^zwei und nach unten zeigen. Bestimmen Sie die Geschwindigkeit der Kugel 2 s und 4 s nach dem Schuss.

Antworten

Die vertikale Richtung wird als positiv angenommen nach oben. UNDIn diesem Fall ist die Beschleunigung der Bewegung gegeben durch

a (t) = -10 m / s^zwei   

Die Geschwindigkeit als Funktion der Zeit wird gegeben durch:

Nach 4 s Abfeuern beträgt die Geschwindigkeit 30 - 10 ∙ 4 = -10 m / s. Dies bedeutet, dass die Kugel bei 4 s mit einer Geschwindigkeit von 10 m / s abfällt.

Verweise

1. Giancoli, D. Physics. Prinzipien mit Anwendungen. 6. Auflage. Prentice Hall. 25-27.
2. Resnick, R. (1999). Körperlich. Band 1. Dritte Ausgabe in Spanisch. Mexiko. Compañía Editorial Continental S.A. de C.V. 22-27.
3. Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7 .. Auflage. Mexiko. Cengage Learning Editors. 25-30.