
Resultierende Vektorberechnung, Beispiele, Übungen
Das resultierender Vektor ist diejenige, die durch eine Operation mit Vektoren erhalten wird, deren Ergebnis auch ein Vektor ist. Normalerweise ist diese Operation die Summe von zwei oder mehr Vektoren, mit denen ein Vektor erhalten wird, dessen Wirkung äquivalent ist.
Auf diese Weise werden Vektoren wie die resultierende Geschwindigkeit, Beschleunigung oder Kraft erhalten. Zum Beispiel, wenn mehrere Kräfte auf einen Körper wirken F.1, F.zwei, F.3,…. Die Vektorsumme aller dieser Kräfte entspricht der Nettokraft (der Resultierenden), die mathematisch wie folgt ausgedrückt wird:
F.1 + F.zwei + F.3 +… = F.R. oder F.N.

Der resultierende Vektor, ob es sich um Kräfte oder eine andere Vektorgröße handelt, wird durch Anwenden der Regeln der Vektoraddition ermittelt. Da die Vektoren zusätzlich zum numerischen Wert eine Richtung und einen Sinn haben, reicht es nicht aus, die Module zu addieren, um den resultierenden Vektor zu erhalten.
Dies gilt nur für den Fall, dass die beteiligten Vektoren in die gleiche Richtung weisen (siehe Beispiele). Andernfalls müssen Vektorsummenmethoden verwendet werden, die je nach Fall geometrisch oder analytisch sein können..
Artikelverzeichnis
- 1 Beispiele
- 1.1 Geometrische Methoden zum Hinzufügen von zwei Vektoren
- 2 Übungen
- 2.1 -Übung 1
- 2.2 Übung 2
- 3 Referenzen
Beispiele
Die geometrischen Methoden zum Finden des resultierenden Vektors sind die polygonale Methode und die Parallelogrammmethode.
Für analytische Methoden gibt es die Komponentenmethode, mit der der aus einem beliebigen Vektorsystem resultierende Vektor gefunden werden kann, vorausgesetzt, wir haben seine kartesischen Komponenten..
Geometrische Methoden zum Hinzufügen von zwei Vektoren
Angenommen, die Vektoren oder Y. v (Wir bezeichnen sie fett, um sie von den Skalaren zu unterscheiden.) In Abbildung 2a) haben wir sie im Flugzeug. In Abbildung 2 b) wurde es so auf den Vektor v übertragen, dass sein Ursprung mit dem Ende von übereinstimmt oder. Der resultierende Vektor geht vom Ursprung des ersten (oder) bis zur Spitze des Letzten (v):
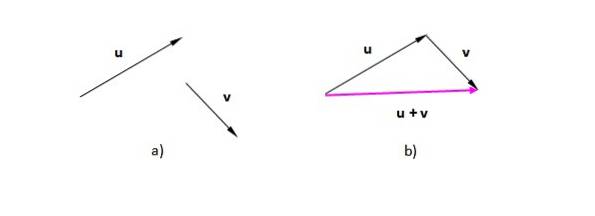
Die resultierende Figur ist in diesem Fall ein Dreieck (ein Dreieck ist ein dreiseitiges Polygon). Wenn wir zwei Vektoren in derselben Richtung haben, ist die Vorgehensweise dieselbe: Platzieren Sie einen der Vektoren nach dem anderen und zeichnen Sie einen, der vom Ursprung oder Schwanz des ersten zur Spitze oder zum Ende des letzten geht.
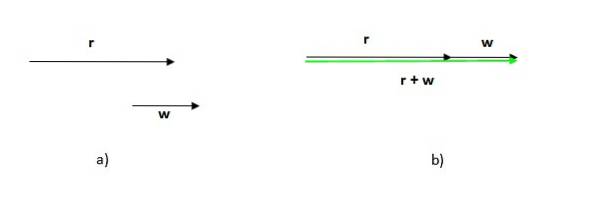
Beachten Sie, dass die Reihenfolge, in der diese Prozedur ausgeführt wird, keine Rolle spielt, da die Summe der Vektoren kommutativ ist.
Beachten Sie auch, dass in diesem Fall die Modul (die Länge oder Größe) des resultierenden Vektors ist die Summe der Module der hinzugefügten Vektoren, im Gegensatz zum vorherigen Fall, in dem das Modul des resultierenden Vektors kleiner ist als die Summe der Module der Teilnehmer.
Parallelogrammmethode
Diese Methode ist sehr geeignet, wenn Sie zwei Vektoren hinzufügen müssen, deren Ursprungspunkte beispielsweise mit dem Ursprung eines x-y-Koordinatensystems übereinstimmen. Angenommen, dies ist bei unseren Vektoren der Fall oder Y. v (Abbildung 3a):
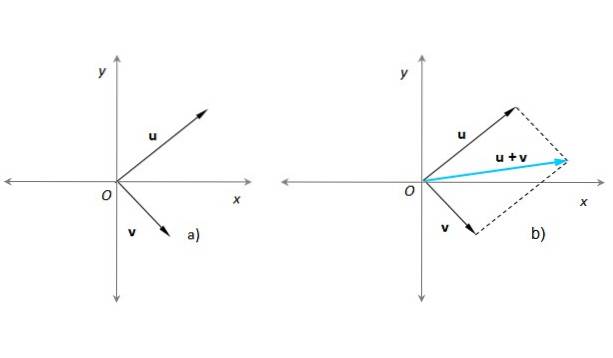
In Abbildung 3b) wurde ein Parallelogramm mit Hilfe von gepunkteten Linien parallel zu erstellt oder bereits v. Der resultierende Vektor hat seinen Ursprung bei O und sein Ende an dem Punkt, an dem sich die gepunkteten Linien schneiden. Dieses Verfahren entspricht vollständig dem im vorherigen Abschnitt beschriebenen..
Ausbildung
-Übung 1
Finden Sie anhand der folgenden Vektoren den resultierenden Vektor mithilfe der Traversenmethode.
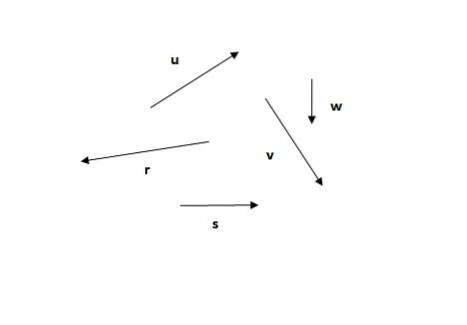
Lösung
Die Traversenmethode ist die erste der beobachteten Methoden. Denken Sie daran, dass die Summe der Vektoren kommutativ ist (die Reihenfolge der Addenden ändert nichts an der Summe), sodass Sie beispielsweise mit einem der Vektoren beginnen können oder (Abbildung 5a) oder r (Abbildung 5b):
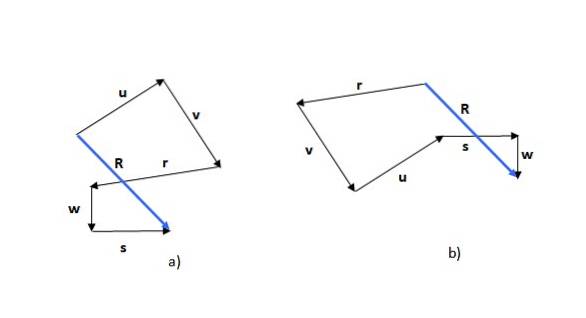
Die erhaltene Figur ist ein Polygon und der resultierende Vektor (in blau) wird aufgerufen R.. Wenn Sie mit einem anderen Vektor beginnen, kann die Form, die gebildet wird, unterschiedlich sein, wie im Beispiel zu sehen ist, aber der resultierende Vektor ist der gleiche.
Übung 2
In der folgenden Abbildung ist bekannt, dass die Module der Vektoren oder Y. v jeweils sind sie u = 3 beliebige Einheiten und v = 1,8 beliebige Einheiten. Der Winkel, der oder Form mit der positiven x-Achse ist 45º, während v es bildet 60º mit der y-Achse, wie in der Abbildung gezeigt. Finden Sie den resultierenden Vektor, die Größe und die Richtung.
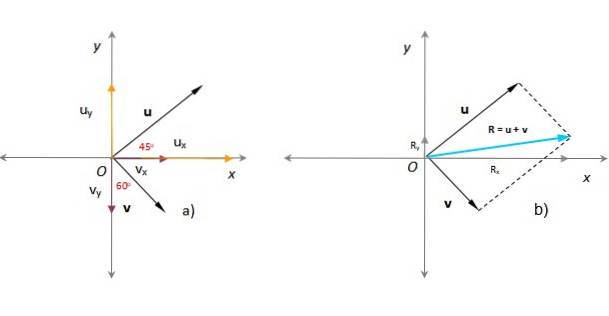
Lösung
Im vorherigen Abschnitt wurde der resultierende Vektor unter Anwendung der Parallelogrammmethode (in der Abbildung in Türkis) gefunden..
Eine einfache Möglichkeit, den resultierenden Vektor analytisch zu finden, besteht darin, die Additionsvektoren in Form ihrer kartesischen Komponenten auszudrücken. Dies ist einfach, wenn Modul und Winkel bekannt sind, wie z. B. die Vektoren in diesem Beispiel:
oderx = u. cos 45º = 3 x cos 45º = 2,12; oderY. = u. sin 45º = 3x sin 45º = 2.12
vx = v. sin 60º = 1,8 x sin 60º = 1,56; vY. = -v. cos 60º = -1,8 x cos 60º = - 0,9
Vektoren oder Y. v Sie sind Vektoren, die zur Ebene gehören und daher jeweils zwei Komponenten aufweisen. Der Vektor u befindet sich im ersten Quadranten und seine Komponenten sind positiv, während sich der Vektor v im vierten Quadranten befindet. seine x-Komponente ist positiv, aber seine Projektion auf die vertikale Achse fällt auf die negative y-Achse.
Berechnung der kartesischen Komponenten des resultierenden Vektors
Der resultierende Vektor wird durch algebraisches Addieren der jeweiligen x- und y-Komponenten gefunden, um ihre kartesischen Komponenten zu erhalten:
R.x = 2,12 + 1,56 = 3,68
R.Y. = 2,12 + (-0,9) = 1,22
Sobald die kartesischen Komponenten spezifiziert wurden, ist der Vektor vollständig bekannt. Der resultierende Vektor kann mit der Notation in eckigen Klammern (Hosenträger):
R = < 3.68; 1.22> beliebige Einheiten
Die Notation in eckigen Klammern wird verwendet, um einen Vektor von einem Punkt in der Ebene (oder im Raum) zu unterscheiden. Eine andere Möglichkeit, den resultierenden Vektor analytisch auszudrücken, besteht in der Verwendung der Einheitsvektoren ich und j in der Ebene (ich, j Y. k Im Weltall):
R. = 3,68 ich + 1.22 j beliebige Einheiten
Da beide Komponenten des resultierenden Vektors positiv sind, ist der Vektor R. gehört zum ersten Quadranten, der schon vorher grafisch gesehen worden war.
Größe und Richtung des resultierenden Vektors
Bei Kenntnis der kartesischen Komponenten wird die Größe von R durch den Satz von Pythagoras berechnet, da der resultierende Vektor R., zusammen mit seinen R-Komponentenx und R.Y. bilden ein rechtwinkliges Dreieck:
Größe oder Modul: R = (3,68zwei + 1.22zwei)½ = 3,88
Richtung q unter Verwendung der positiven x-Achse als Referenz: q = Arctan (R.Y. / R.x) = arctg (1,22 / 3,68) = 18,3 º
Verweise
- Hinzufügen von Vektoren und Regeln. Abgerufen von: newt.phys.unsw.edu.au
- Figueroa, D. Reihe: Physik für Naturwissenschaften und Technik. Band 1. Kinematik. 31-68.
- Körperlich. Modul 8: Vektoren. Wiederhergestellt von: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanik für Ingenieure. Statisch. 6. Auflage. Continental Verlag. 15-53.
- Vektoradditionsrechner. Abgerufen von: www.1728.org


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.