
Ausgleichsvektorberechnung, Beispiele, Übungen
Das Ausgleichsvektor Es ist dasjenige, das dem resultierenden Vektor entgegengesetzt ist und daher in der Lage ist, ein System auszugleichen, da es die gleiche Größe und die gleiche Richtung hat, aber die entgegengesetzte Richtung dazu.
In vielen Fällen bezieht sich der Ausgleichsvektor auf einen Kraftvektor. Um die Ausgleichskraft zu berechnen, ermitteln Sie zunächst die resultierende Kraft, wie in der folgenden Abbildung dargestellt:
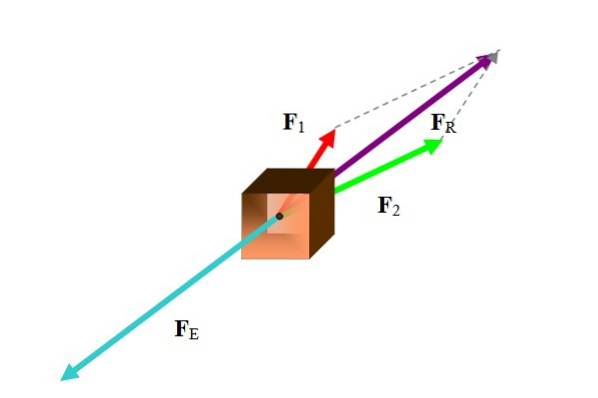
Abhängig von den vorliegenden Daten gibt es verschiedene Methoden, um diese Aufgabe auszuführen. Da die Kräfte Vektoren sind, ergibt sich die Vektorsumme der beteiligten Kräfte:
F.R. = F.1 + F.zwei + F.3 + ... .
Zu den zu verwendenden Methoden gehören grafische Methoden wie Polygon-, Parallelogramm- und Analysemethoden wie die Zerlegung von Kräften in ihre kartesischen Komponenten. Im Beispiel wurde in der Abbildung die Parallelogrammmethode verwendet.
Sobald die resultierende Kraft gefunden wurde, ist die Ausgleichskraft genau der entgegengesetzte Vektor.
Ja F.UND ist die ausgleichende Kraft, dann ist es zufrieden, dass F.UND An einem bestimmten Punkt angewendet, garantiert es das Translationsgleichgewicht des Systems. Wenn es sich um ein einzelnes Teilchen handelt, bewegt es sich nicht (oder möglicherweise mit konstanter Geschwindigkeit), aber wenn es sich um ein erweitertes Objekt handelt, kann es sich trotzdem drehen:
F.R. + F.UND = 0
Artikelverzeichnis
- 1 Beispiele
- 1.1 Krafttabelle
- 2 Gelöste Übungen
- 2.1 -Übung 1
- 2.2 -Übung 2
- 3 Referenzen
Beispiele
Überall sind ausgleichende Kräfte vorhanden. Wir selbst werden durch die Kraft ausgeglichen, die der Stuhl ausübt, um das Gewicht auszugleichen. Die ruhenden Objekte: Bücher, Möbel, Deckenleuchten und eine Vielzahl von Mechanismen werden ständig durch Kräfte ausgeglichen.
Zum Beispiel wird ein ruhendes Buch auf einem Tisch durch die normale Kraft ausgeglichen, die es auf das Buch ausübt, wodurch verhindert wird, dass es herunterfällt. Das gleiche passiert mit der Kette oder dem Kabel, mit dem die Lampe in einem Raum von der Decke hängt. Die Kabel, die eine Last halten, verteilen ihr Gewicht durch die Spannung in ihnen.
In einer Flüssigkeit können einige Objekte schweben und in Ruhe bleiben, da ihr Gewicht durch eine von der Flüssigkeit ausgeübte Aufwärtskraft ausgeglichen wird drücken.
Verschiedene Mechanismen müssen unter Kenntnis des Ausgleichskraftvektors wie Stangen, Balken und Säulen ausgeglichen werden.
Bei Verwendung einer Waage ist es notwendig, das Gewicht des Objekts mit einer äquivalenten Kraft auszugleichen, entweder durch Hinzufügen von Gewichten oder durch Federn..
Krafttabelle
Die Krafttabelle wird im Labor verwendet, um die Ausgleichskraft zu bestimmen. Es besteht aus einer kreisförmigen Plattform, von der Sie die Draufsicht in der Abbildung haben und die einen Winkelmesser zum Messen von Winkeln hat.
An den Tischkanten befinden sich Riemenscheiben, durch die Seile mit Gewichten verlaufen und die in einem Ring in der Mitte zusammenlaufen.
Zum Beispiel werden zwei Gewichte aufgehängt. Die durch diese Gewichte in den Saiten erzeugten Spannungen sind in Abbildung 2 in Rot und Blau dargestellt. Ein drittes Gewicht in Grün kann die resultierende Kraft der beiden anderen ausgleichen und das System im Gleichgewicht halten..
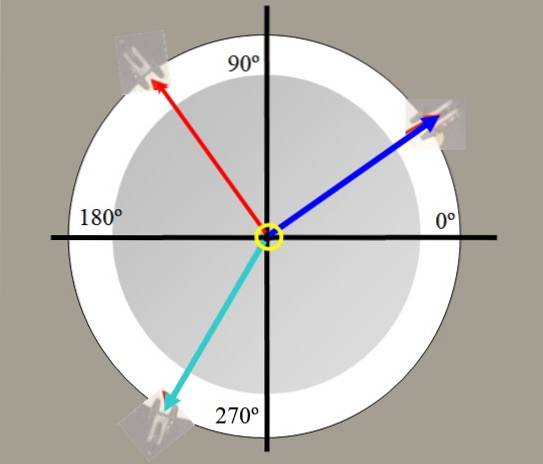
Mit der Krafttabelle ist es möglich, den Vektorcharakter der Kräfte zu verifizieren, Kräfte zu zerlegen, die Ausgleichskraft zu finden und den Satz von Lamy zu verifizieren:
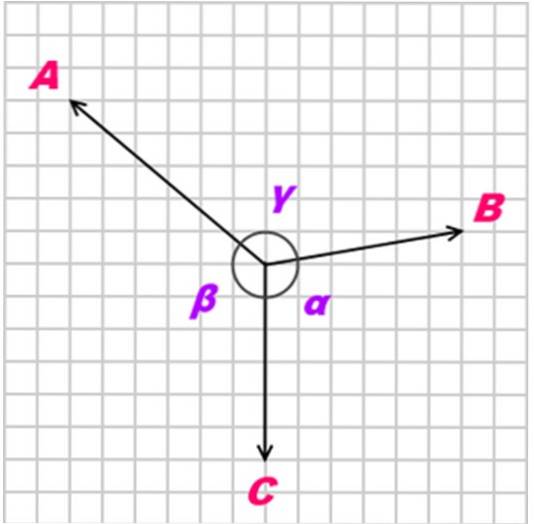
Wenn ein Der Körper befindet sich dank der drei koplanaren Kräfte, die gleichzeitig und nicht kollinear (nicht parallel) genannt werden, im Gleichgewicht ZU, B. Y. C., Die Beziehung zwischen diesen Kräften ist wie folgt:
A / sin α = B / sin β = C / sin γ
Gelöste Übungen
-Übung 1
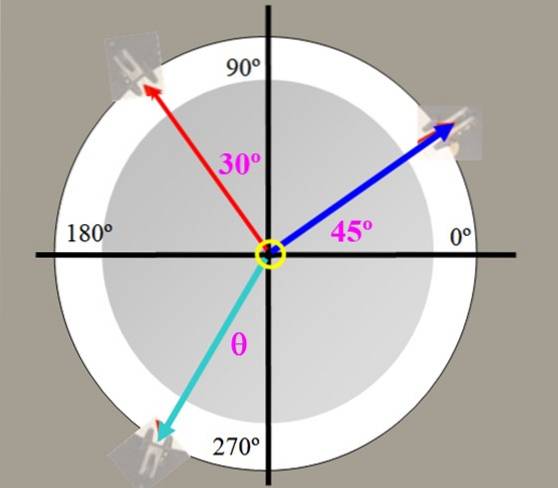
Gewichte von 225 g (blaue Spannung) und 150 g (rote Spannung) werden mit den gezeigten Winkeln an die Krafttabelle von Fig. 2 gehängt. Finden Sie den Wert der Ausgleichskraft und den Winkel, den sie mit der vertikalen Achse bildet.
Lösung
Das Problem kann mit den in Gramm (Kräften) ausgedrückten Gewichten gelöst werden. Lassen Sie P.1 = 150 Gramm und P.zwei = 225 Gramm, die jeweiligen Komponenten von jedem sind:
P.1x = 225. cos 45 ° g = 159,10 g; P.1y = 225. cos 45º g = 159,10 g
P.2x = -150. sin 30 g = -75,00 g; P.2 und = 150. cos 30º g = 129,90 g
Das resultierende Gewicht P.R. wird durch algebraisches Hinzufügen der Komponenten gefunden:
P.Rx = 159,10 - 75,00 g = 84,10 g
P.Ry = 159,10 + 129,90 g = 289,00 g
Das Ausgleichsgewicht P.UND ist der gegenüberliegende Vektor P.R.::
P.Ehemalige = -84,10 g
P.Hallo = -289,00 g
Die Größe des Ausgleichsgewichts wird berechnet durch:
P.UND = (P.Ehemaligezwei + P.Hallozwei)1/2 = ((-84,10)zwei + (-289,00)zwei)1/2 g = 301 g
Der Winkel θ in der Figur ist:
θ = arctg (-84,10 / -289,00) = 16,2º in Bezug auf die Achse Y. Negativ.
-Übung 2
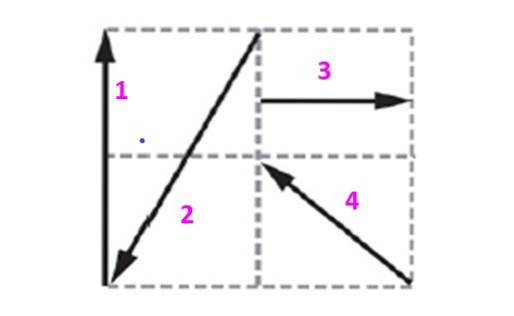
Finden Sie den Ausgleichsvektor des in der Abbildung gezeigten Systems, wobei Sie wissen, dass jedes Quadrat 10 m auf einer Seite misst.
Lösung
Die in diesem Gitter enthaltenen Vektoren werden als Einheits- und orthogonale Vektoren ausgedrückt ich Y. j das bestimmt das Flugzeug. Vektor 1, der als bezeichnet wird v1 es hat eine Größe von 20 m und ist vertikal nach oben gerichtet. Es kann ausgedrückt werden als:
v1 = 0 ich +zwanzig j m
Aus der Zeichnung ist ersichtlich, dass Vektor 2 ist:
vzwei = -10 ich - zwanzig j m
Vektor 3 ist horizontal und zeigt in die positive Richtung:
v3 = 10 ich + 0 j m
Schließlich ist der Vektor 4 um 45 ° geneigt, da er die Diagonale des Quadrats ist, weshalb seine Komponenten dasselbe messen:
v4 = -10 ich + 10 j m
Beachten Sie, dass die Vorzeichen angeben, auf welcher Seite der Achse sich die Komponenten befinden: Oben und rechts haben sie ein + -Zeichen, während sie unten und links ein Vorzeichen haben -.
Der resultierende Vektor wird durch Hinzufügen von Komponente zu Komponente erhalten:
vR. = -10 ich + 10 j m
Dann ist der Ausgleichsvektor des Systems:
vUND = 10 ich - 10 j m
Verweise
- Beardon, T. 2011. Eine Einführung in Vektoren. Abgerufen von: nrich.maths.org.
- Bedford, 2000. A. Technische Mechanik: Statik. Addison Wesley. 38-52.
- Figueroa, D. Reihe: Physik für Naturwissenschaften und Technik. Band 1. Kinematik. 31-68.
- Körperlich. Modul 8: Vektoren. Wiederhergestellt von: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mechanik für Ingenieure. Statisch. 6. Auflage. Continental Verlag. 15-53.
- Vektoradditionsrechner. Wiederhergestellt von: 1728.org
- Vektoren. Wiederhergestellt von: wikibooks.org



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.