
Vektorlenkungsgleichung der Linie, gelöste Übungen
Es wird verstanden von Regisseur Vektor eine, die die Richtung einer Linie entweder in der Ebene oder im Raum definiert. Daher kann ein Vektor parallel zur Linie als ein Richtungsvektor desselben betrachtet werden.
Dies ist möglich dank eines Axioms der euklidischen Geometrie, das besagt, dass zwei Punkte eine Linie definieren. Dann definiert das durch diese beiden Punkte gebildete orientierte Segment auch einen Direktorvektor dieser Linie.
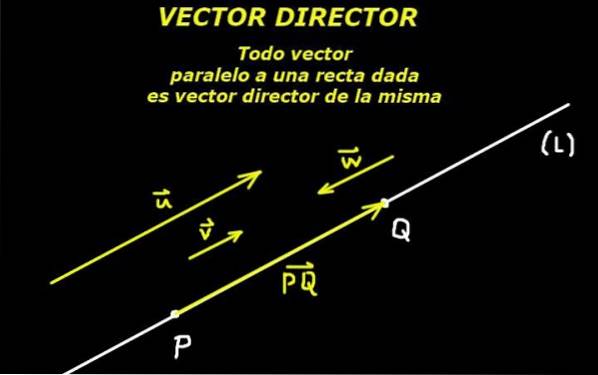
Gegeben einen Punkt P. Zugehörigkeit zur Linie (L) und einen Director-Vektor gegeben oder von dieser Linie ist die Linie vollständig bestimmt.
Artikelverzeichnis
- 1 Gleichung von Linie und Direktorvektor
- 1.1 Parametrische Gleichung der Linie
- 2 Die Linie in Vektorform
- 2.1 Beispiel 2
- 2.2 Kontinuierliche Form der Linie und des Direktorvektors
- 3 Allgemeine Form der Liniengleichung
- 3.1 Beispiel 3
- 4 Standardform der Liniengleichung
- 4.1 Beispiel 4
- 5 Übungen gelöst
- 5.1 -Übung 1
- 5.2 -Übung 2
- 6 Referenzen
Gleichung der Linie und des Direktorvektors
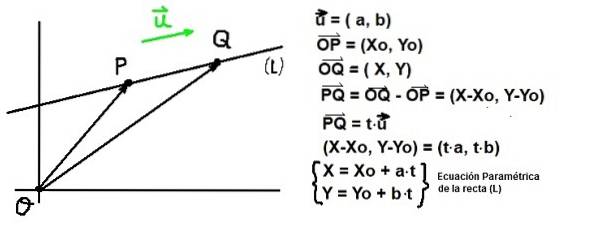
Gegeben einen Punkt P. von Koordinaten F: (Xo, I) und ein Vektor oder Regisseur einer Straße (L), alles Punkt Q. von Koordinaten F: (X, Y) muss erfüllen, dass der Vektor PQ sei parallel zu u. Diese letzte Bedingung ist garantiert, wenn PQ ist proportional zu oder::
PQ = t⋅oder
im vorherigen Ausdruck t ist ein Parameter, der zu den reellen Zahlen gehört.
Wenn die kartesischen Komponenten von PQ und von oder Die obige Gleichung ist wie folgt geschrieben:
(X-Xo, Y-Yo) = t⋅ (a, b)
Wenn die Komponenten der Vektorgleichheit ausgeglichen sind, haben wir das folgende Gleichungspaar:
X - Xo = a⋅t Y. Y - I = b⋅t
Parametrische Gleichung der Linie
Die Koordinaten X. und Y. eines Punktes auf der Linie (L) durch einen Koordinatenpunkt gehen (Xo, ich) und es ist parallel zu Regisseur Vektor oder= (a, b) werden bestimmt, indem dem variablen Parameter t reelle Werte zugewiesen werden:
X = Xo + a⋅t; Y = I + b⋅t
Beispiel 1
Um die Bedeutung der parametrischen Gleichung der Linie zu veranschaulichen, nehmen wir als Richtungsvektor
oder = (a, b) = (2, -1)
und als bekannter Punkt der Linie der Punkt
P = (Xo, I) = (1, 5).
Die parametrische Gleichung der Linie lautet:
X = 1 + 2⋅t; Y = 5 - 1 · t; -∞
Zur Veranschaulichung der Bedeutung dieser Gleichung ist Abbildung 3 dargestellt, in der sich der Wert und der Punkt des Parameters t ändern Q. von Koordinaten (X, Y) Nehmen Sie verschiedene Positionen auf der Geraden ein.
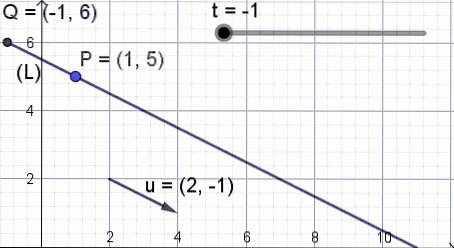
Die Linie in Vektorform
Wenn ein Punkt P auf der Linie und sein Direktorvektor u gegeben sind, kann die Gleichung der Linie in Vektorform geschrieben werden:
OQ = OP + λ⋅oder
In der obigen Gleichung ist Q ein beliebiger Punkt, der jedoch zur Linie und gehört λ eine reelle Zahl.
Die Vektorgleichung der Linie ist auf eine beliebige Anzahl von Dimensionen anwendbar, sogar eine Hyperlinie kann definiert werden.
Im dreidimensionalen Fall für einen Direktorvektor oder= (a, b, c) und ein Punkt P = (Xo, Yo, Zo), die Koordinaten eines generischen Punktes Q = (X, Y, Z) Zugehörigkeit zur Linie ist:
(X UND Z) = (Xo, Yo, Zo) + λ⋅ (a, b, c)
Beispiel 2
Betrachten Sie noch einmal die Linie, die als Richtungsvektor gilt
oder = (a, b) = (2, -1)
und als bekannter Punkt der Linie der Punkt
P = (Xo, I) = (1, 5).
Die Vektorgleichung dieser Linie lautet:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Kontinuierliche Form der Linie und des Direktorvektors
Ausgehend von der parametrischen Form, die den Parameter λ löscht und gleichsetzt, haben wir:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
Dies ist die symmetrische Form der Liniengleichung. Ich fühle, dass zu, b Y. c sind die Komponenten des Director-Vektors.
Beispiel 3
Betrachten Sie die Linie als Richtungsvektor
oder = (a, b) = (2, -1)
und als bekannter Punkt der Linie der Punkt
P = (Xo, I) = (1, 5). Finden Sie seine symmetrische Form.
Die symmetrische oder kontinuierliche Form der Linie ist:
(X - 1) / 2 = (Y - 5) / (- 1)
Allgemeine Form der Liniengleichung
Die Gleichung mit der folgenden Struktur ist als allgemeine Form der Linie in der XY-Ebene bekannt:
A⋅X + B⋅Y = C.
Der Ausdruck für die symmetrische Form kann so umgeschrieben werden, dass er die allgemeine Form hat:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
im Vergleich zur allgemeinen Form der Linie ist es:
A = b, B = -a und C = b⋅Xo - a⋅Yo
Beispiel 3
Finden Sie die allgemeine Form der Linie, deren Direktorvektor u = (2, -1) ist.
und das geht durch den Punkt P = (1, 5).
Um die allgemeine Form zu finden, können wir die angegebenen Formeln verwenden, es wird jedoch ein alternativer Pfad gewählt.
Wir beginnen damit, den Doppelvektor w des Direktorvektors u zu finden, der als der Vektor definiert ist, der durch Austauschen der Komponenten von u und Multiplizieren des zweiten mit -1 erhalten wird:
w= (-1, -2)
der duale Vektor w entspricht einer Drehung des Direktorvektors um 90 ° im Uhrzeigersinn v.
Wir multiplizieren skalar w mit (X, Y) und mit (Xo, ich) und wir passen zusammen:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2⋅5 = -11
bleibt endlich:
X + 2Y = 11
Standardform der Liniengleichung
Es ist als Standardform der Linie in der XY-Ebene bekannt, die die folgende Struktur aufweist:
Y = m⋅X + d
Dabei steht m für die Steigung und d für den Schnittpunkt mit der Y-Achse.
Bei gegebenem Richtungsvektor u = (a, b) ist die Steigung m b / a.
Y d wird erhalten, indem der bekannte Punkt Xo, I durch X und Y ersetzt wird:
I = (b / a) Xo + d.
Kurz gesagt, m = b / a und d = I - (b / a) Xo
Beachten Sie, dass die Steigung m der Quotient zwischen den Komponenten ist Y. des Direktorvektors und der Komponente x von dem selben.
Beispiel 4
Finden Sie die Standardform der Linie, deren Direktorvektor u = (2, -1) ist.
und das geht durch den Punkt P = (1, 5).
m = -½ und d = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Gelöste Übungen
-Übung 1
Finden Sie einen Direktorvektor der Linie (L), der der Schnittpunkt der Ebene (Π) ist: X - Y + Z = 3 und der Ebene (Ω): 2X + Y = 1.
Schreiben Sie dann die stetige Form der Gleichung der Linie (L).
Lösung
Aus der Gleichung der Ebene (Ω) Abstand Y: Y = 1 -2X
Dann setzen wir in die Gleichung der Ebene (Π) ein:
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Dann parametrisieren wir X, wir wählen die Parametrierung X = λ
Dies bedeutet, dass die Linie eine Vektorgleichung hat, die gegeben ist durch:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
die umgeschrieben werden kann als:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
womit klar ist, dass der Vektor oder = (1, -2, -3) ist ein Richtungsvektor der Linie (L).
Die durchgehende Form der Linie (L) ist:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Übung 2
Angesichts der 5X-Ebene + zu Y + 4Z = 5
und die Linie, deren Gleichung X / 1 = (Y-2) / 3 = (Z-2) / (-2) ist
Bestimmen Sie den Wert von zu so dass die Ebene und die Linie parallel sind.
Lösung 2
Der Vektor n = (5, a, 4) ist ein Vektor senkrecht zur Ebene.
Der Vektor oder = (1, 3, -2) ist ein Direktorvektor der Linie.
Wenn die Linie parallel zur Ebene ist, dann n • v = 0.
(5, zu, 4)• •(1, 3, -2) = 5 +3zu -8 = 0 ⇒ zu= 1.
Verweise
- Fleming, W. & Varberg, D. E. (1989). Precalculus Mathematik. Prentice Hall PTR.
- Kolman, B. (2006). Lineare Algebra. Pearson Ausbildung.
- Leal, J. M. & Viloria, N. G. (2005). Flugzeuganalytische Geometrie. Mérida - Venezuela: Editorial Venezolana C. A..
- Navarro, Rocio. Vektoren. Wiederhergestellt von: books.google.co.ve.
- Pérez, C. D. (2006). Vorberechnung. Pearson Ausbildung.
- Prenowitz, W. 2012. Grundlegende Konzepte der Geometrie. Rowman & Littlefield.
- Sullivan, M. (1997). Vorberechnung. Pearson Ausbildung.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.