Flugbahn in physikalischen Eigenschaften, Typen, Beispielen und Übungen

Das Flugbahn in der Physik Es ist die Kurve, die ein Mobiltelefon beschreibt, wenn es während seiner Bewegung aufeinanderfolgende Punkte durchläuft. Da es eine unendliche Anzahl von Varianten annehmen kann, werden auch die Trajektorien, denen das Mobiltelefon folgen kann, verwendet.

Um von einem Ort zum anderen zu gelangen, kann eine Person verschiedene Wege und Wege gehen: zu Fuß durch die Bürgersteige in Straßen und Alleen oder mit dem Auto oder Motorrad auf einer Autobahn. Während eines Waldspaziergangs kann der Wanderer einem komplizierten Pfad folgen, der Kurven umfasst, in der Ebene auf- oder absteigt und sogar mehrmals denselben Punkt passiert.

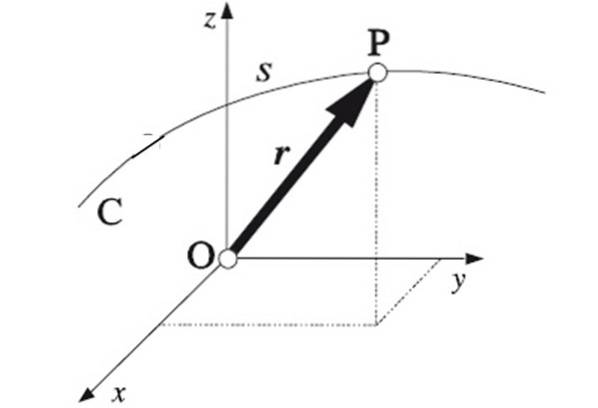
Wenn die Punkte, durch die das Mobiltelefon fährt, einer geraden Linie folgen, ist die Flugbahn geradlinig. Dies ist der einfachste Weg, da er eindimensional ist. Die Angabe der Position erfordert eine einzelne Koordinate.

Das Mobiltelefon kann jedoch einem krummlinigen Pfad folgen und geschlossen oder geöffnet werden. In diesen Fällen erfordert die Verfolgung der Position zwei oder drei Koordinaten. Dies sind Bewegungen in der Ebene bzw. im Raum. Das hat damit zu tun Links: Materialbedingungen, die die Bewegung einschränken. Einige Beispiele sind:

- Die Umlaufbahnen, die die Planeten um die Sonne beschreiben, sind geschlossene ellipsenförmige Pfade. Obwohl sie in einigen Fällen wie im Fall der Erde einem Kreis angenähert werden können.

- Der Ball, den der Torhüter bei einem Abstoß tritt, folgt einer parabolischen Flugbahn.

- Ein Vogel im Flug beschreibt krummlinige Flugbahnen im Weltraum, da er sich nicht nur in einem Flugzeug bewegen kann, sondern auch nach Belieben in der Ebene nach oben oder unten gehen kann.

Die Flugbahn in der Physik kann mathematisch ausgedrückt werden, wenn die Position des Mobiltelefons zu jedem Zeitpunkt bekannt ist. Sein r der Positionsvektor, der wiederum Koordinaten hat x, Y. Y. z im allgemeinsten Fall einer Bewegung in drei Dimensionen. Die Funktion kennen r (t) Die Flugbahn wird vollständig bestimmt.

Artikelverzeichnis

• 1 Typen
  • 1.1 Bewegungen in einer, zwei und drei Dimensionen
• 2 Beispiele
  • 2.1 Pfad eines Mobiltelefons auf explizite, implizite und parametrische Weise
• 3 Gelöste Übungen
  • 3.1 Gelöste Übung 1
  • 3.2 Aufgabe gelöst 2
  • 3.3 Aufgabe gelöst 3
• 4 Referenzen

Typen

Im Allgemeinen kann die Trajektorie eine ziemlich komplizierte Kurve sein, insbesondere wenn Sie sie mathematisch ausdrücken möchten. Aus diesem Grund beginnt es mit den einfachsten Modellen, bei denen die Handys auf einer geraden Linie oder in einem Flugzeug fahren, bei dem es sich um den Boden oder ein anderes geeignetes Modell handeln kann:

Bewegungen in einer, zwei und drei Dimensionen

Die am besten untersuchten Flugbahnen sind:

- Geradlinig, wenn Sie auf einer geraden horizontalen, vertikalen oder geneigten Linie fahren. Ein Ball, der vertikal nach oben geworfen wird, folgt diesem Pfad, oder ein Objekt, das eine Steigung hinuntergleitet, folgt. Es sind eindimensionale Bewegungen, wobei eine einzige Koordinate ausreicht, um ihre Position vollständig zu bestimmen..

- Parabolisch, in dem das Handy einen Bogen einer Parabel beschreibt. Es ist häufig, da jedes Objekt, das unter der Einwirkung der Schwerkraft schräg geworfen wird (ein Projektil), dieser Flugbahn folgt. Um die Position des Mobiltelefons festzulegen, müssen Sie zwei Koordinaten angeben: x Y. Y..

- Kreisförmig, tritt auf, wenn das sich bewegende Teilchen einem Kreis folgt. Es ist auch in der Natur und in der täglichen Praxis üblich. Viele Alltagsgegenstände folgen einer Kreisbahn wie Reifen, Maschinenteile und umlaufende Satelliten, um nur einige zu nennen..

- Elliptisch, Das Objekt bewegt sich nach einer Ellipse. Wie eingangs gesagt, ist dies der Weg, dem die Planeten im Orbit um die Sonne folgen.

- Hyperbolisch, Astronomische Objekte, die unter der Wirkung einer zentralen Kraft (Schwerkraft) stehen, können elliptischen (geschlossenen) oder hyperbolischen (offenen) Trajektorien folgen, die weniger häufig sind als die ersteren.

- Helical, oder Spiralbewegung, wie die eines Vogels, der in einem thermischen Strom aufsteigt.

- Schaukel oder Pendel, Das Handy beschreibt einen Bogen in Hin- und Herbewegungen.

Beispiele

Die im vorherigen Abschnitt beschriebenen Trajektorien sind sehr nützlich, um schnell eine Vorstellung davon zu bekommen, wie sich ein Objekt bewegt. In jedem Fall muss klargestellt werden, dass die Flugbahn eines Mobiltelefons vom Standort des Beobachters abhängt. Dies bedeutet, dass dasselbe Ereignis auf unterschiedliche Weise gesehen werden kann, je nachdem, wo sich jede Person befindet..

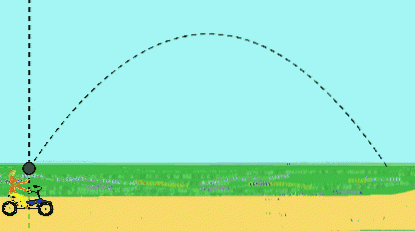
Zum Beispiel tritt ein Mädchen mit konstanter Geschwindigkeit in die Pedale und wirft einen Ball nach oben. Sie beobachtet, dass der Ball einen geradlinigen Weg beschreibt. 

Für einen Beobachter, der auf der Straße steht und sieht, wie sie vorbeigeht, hat der Ball jedoch eine parabolische Bewegung. Für ihn wurde der Ball zunächst mit einer geneigten Geschwindigkeit geworfen, was sich aus der Geschwindigkeit der Hand des Mädchens nach oben und der Geschwindigkeit des Fahrrads ergibt..

Pfad eines Mobiltelefons auf explizite, implizite und parametrische Weise

- Explizit, direkte Angabe der durch die Gleichung gegebenen Kurve oder des Ortes y (x)

- Implizit, in dem eine Kurve ausgedrückt wird als f (x, y, z) = 0

-Parametrisch, In dieser Form werden die x-, y- und z-Koordinaten als Funktion eines Parameters angegeben, der im Allgemeinen als Zeit gewählt wird t. In diesem Fall besteht die Flugbahn aus folgenden Funktionen: x (t), und T) Y. z (t).

Als nächstes werden zwei Trajektorien detailliert beschrieben, die in der Kinematik umfassend untersucht wurden: die parabolische Trajektorie und die kreisförmige Trajektorie..

Gekippter Start ins Vakuum

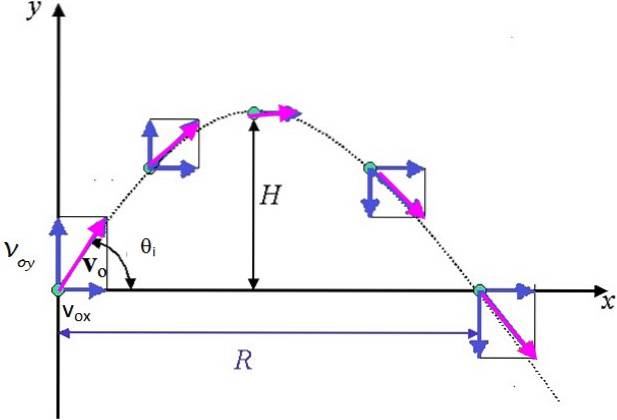
Ein Objekt (das Projektil) wird in einem Winkel a zur Horizontalen und mit Anfangsgeschwindigkeit geworfen v_oder wie das Bild zeigt. Luftwiderstand wird nicht berücksichtigt. Die Bewegung kann als zwei unabhängige und gleichzeitige Bewegungen behandelt werden: eine horizontale mit konstanter Geschwindigkeit und die andere vertikal unter Einwirkung der Schwerkraft..

x (t) = x_oder +v_Ochse.t

y (t) = y_oder +v_Hallo.t-½ g.t.^zwei

Diese Gleichungen sind parametrische Gleichungen Projektilstart. Wie oben erläutert, haben sie den Parameter t, Was ist Zeit.

Im rechten Dreieck der Abbildung ist Folgendes zu sehen:

v_Ochse = v_oder cos θ_ich

v_Hallo = v_oder sen θ_ich

Das Einsetzen dieser Gleichungen, die den Startwinkel enthalten, in die parametrischen Gleichungen führt zu folgenden Ergebnissen:

x (t) = x_oder +v_oder cos θ_ich.t

y (t) = y_oder +v_oder. sen θ_ich.t -½g.t^zwei

Gleichung des parabolischen Weges

Die explizite Gleichung des Pfades wird gefunden, indem t aus der Gleichung für x (t) gelöst und y (t) durch die Gleichung ersetzt wird. Um die algebraische Arbeit zu erleichtern, kann davon ausgegangen werden, dass sich der Ursprung (0,0) am Startpunkt befindet und somit x_oder = und_oder = 0.

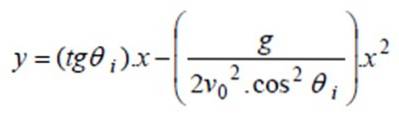
Dies ist die Gleichung des Pfades in expliziter Weg.

Kreisförmiger Pfad

Eine Kreisbahn ist gegeben durch:

(x - x_oder)^zwei + (und und_oder)^zwei = R.^zwei

Hier x_oder und und_oder stellen den Mittelpunkt des vom Mobiltelefon beschriebenen Kreises dar und R ist sein Radius. P (x, y) ist ein Punkt auf dem Pfad. Aus dem schattierten rechtwinkligen Dreieck (Abbildung 3) ist ersichtlich, dass:

x = R. cos θ

y = R. sin θ

Der Parameter ist in diesem Fall der Wobbelwinkel θ, der als Winkelverschiebung bezeichnet wird. In dem speziellen Fall, dass die Winkelgeschwindigkeit & ohgr; (Winkel, der pro Zeiteinheit gewobbelt wird) konstant ist, kann festgestellt werden, dass:

θ = θ_oder + ωt

Wo θ_oder ist die anfängliche Winkelposition des Partikels, die sich, wenn sie als 0 angenommen wird, auf Folgendes reduziert:

θ = ωt

In einem solchen Fall kehrt die Zeit zu parametrischen Gleichungen zurück wie:

x = R.cos ωt

y = R. sin ωt

Die Einheitsvektoren ich Y. j sind sehr praktisch zum Schreiben der Positionsfunktion eines Objekts r (t). Sie geben die Richtungen auf der Achse an x und auf der Achse Y. beziehungsweise. In seinen Begriffen ist die Position eines Teilchens, das eine gleichmäßige Kreisbewegung beschreibt ,:

r (t) = R.cos ωt ich + R. sen ωt j

Gelöste Übungen

Gelöste Übung 1

Eine Kanone kann eine Kugel mit einer Geschwindigkeit von 200 m / s und einem Winkel von 40 ° zur Horizontalen abfeuern. Wenn der Wurf auf ebenem Boden liegt und der Luftwiderstand vernachlässigt wird, finden Sie:

a) Die Gleichung des Pfades y (x) ...

b) Parametrische Gleichungen x (t) Y. und T).

c) Die horizontale Reichweite und die Zeit, die das Projektil in der Luft hält.

d) Die Höhe, in der sich das Projektil befindet, wenn x = 12.000 m

Lösung für)

a) Um die Flugbahn zu finden, werden die in der Gleichung y (x) des vorherigen Abschnitts angegebenen Werte ersetzt:

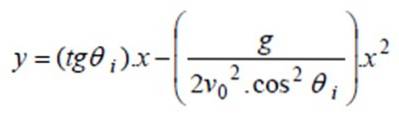
y (x) = tg 40º. x - 9,8 / (2 '400^zwei. cos^zwei40.) x^zwei ⇒  y (x) = 0,8391 x - 0,0000522x^zwei

Lösung b)

b) Der Startpunkt wird am Ursprung des Koordinatensystems (0,0) gewählt:

x (t) = x_oder +v_Ochse.t = 400cos 40º.t = 306,42. t.

y (t) = y_oder +v_Hallo.t-½ g.t.^zwei= 400 'sin 40º.t - 0.5 9.8't^zwei= 257,12 t - 4,9 t^zwei

Lösung c)

c) Um die Zeit zu ermitteln, die das Projektil in der Luft hält, tun Sie dies y (t) = 0, Der Start erfolgt auf ebenem Boden:

0 = 257.12.t - 4.9.t.^zwei

t = 257,12 / 4,9 s = 52,473 s

Die maximale horizontale Reichweite wird durch Einsetzen dieses Wertes in ermittelt x (t):

x_max = 306,4252,47 m = 16077,7 m

Ein anderer Weg, um x zu finden_max direkt ist, indem y = 0 in der Gleichung des Pfades gemacht wird:

0 = 0,8391 x_max - 0,0000522 x^zwei_max

x = 0,8391 / 0,0000522 m = 16078,5 m

Es gibt einen kleinen Unterschied aufgrund der Rundung der Dezimalstellen.

Lösung d)

d) Um die Höhe bei x = 12000 m zu ermitteln, wird dieser Wert direkt in die Pfadgleichung eingesetzt:

und (12000) = 0,8391'12000 - 0,0000522'12000^zwei m = 2552,4 m

Übung gelöst 2

Die Positionsfunktion eines Objekts ist gegeben durch:

r (t) = 3t ich + (4 - 5 t^zwei) j m

Finden:

a) Die Gleichung für den Pfad. Was für eine Kurve ist?

b) Die Ausgangsposition und die Position bei t = 2 s.

c) Die Verschiebung nach t = 2 s.

Lösung

a) Die Positionsfunktion wurde in Bezug auf die Einheitsvektoren angegeben ich Y. j, welche jeweils die Richtung auf den Achsen bestimmen x Y. Y., So:

x (t) = 3t

und T) = 4 -5t^zwei

Die Gleichung des Pfades y (x) klärt sich t von x (t) und ersetzen in y (t):

t = x / 3

y (x) = 4 & ndash; 5. (x / 3)^zwei = 4 - 5x^zwei/ 9 (Gleichnis)

b) Die Ausgangsposition ist: r (2) = 4 j m ;; die Position in t = 2 s es ist r (2) = 6 ich -16 j m

c) Verschiebung D.r ist die Subtraktion der beiden Positionsvektoren:

Δr = r (zwei) - r (2) = 6 ich -16 j- 4 j = 6 ich - zwanzig j m

Übung gelöst 3

Die Erde hat einen Radius R = 6300 km und es ist bekannt, dass die Rotationsperiode ihrer Bewegung um ihre Achse einen Tag beträgt. Finden:

a) Die Gleichung der Flugbahn eines Punktes auf der Erdoberfläche und seiner Positionsfunktion.

b) Die Geschwindigkeit und Beschleunigung dieses Punktes.

Lösung für)

a) Die Positionsfunktion für jeden Punkt in der Kreisbahn lautet:

r (t) = R.cos ωt ich + R.sen ωt j

Wir haben den Radius der Erde R, aber nicht die Winkelgeschwindigkeit ω, sie kann jedoch aus der Periode berechnet werden, da wir wissen, dass für Kreisbewegungen Folgendes gültig ist:

ω = 2π × Frequenz = 2π / Zeitraum

Die Bewegungsdauer beträgt: 1 Tag = 24 Stunden = 1440 Minuten = 86 400 Sekunden, daher:

ω =  2π / 86400 s = 0,000023148 ​​s^-1

Einsetzen in die Positionsfunktion:

r (t) = R.cos ωt ich + R. sen ωt j = 6300 (cos 0,000023148t ich + sen 0,000023148t j) Km

Der Pfad in parametrischer Form lautet:

x (t) = 6300. cos 0,000023148t

y (t) = 6300. sin 0,000023148t

Lösung b)

b) Für Kreisbewegungen die Größe der Lineargeschwindigkeit v eines Punktes hängt mit der Winkelgeschwindigkeit zusammen w durch:

v = ωR = 0,000023148 ​​s^-16300 km = 0,1458 km / s = 145,8 m / s

Sogar eine Bewegung mit konstanter Geschwindigkeit von 145,8 m / s, Es gibt eine Beschleunigung, die in Richtung der Mitte der Kreisbahn zeigt, um den Punkt in Rotation zu halten. Es ist die zentripetale Beschleunigung zu_c, gegeben durch:

zu_c = v^zwei / R = (145,8 m / s)^zwei / 6300 × 10³ m = 0,00337 m / s^zwei.

Verweise

1. Giancoli, D. Physics. (2006). Prinzipien mit Anwendungen. 6^th Prentice Hall. 22-25.
2. Kirkpatrick, L. 2007. Physik: Ein Blick auf die Welt. 6^ta Verkürzte Ausgabe. Lernen einbinden. 23 - 27.
3. Resnick, R. (1999). Körperlich. Band 1. Dritte Ausgabe in Spanisch. Mexiko. Compañía Editorial Continental S.A. de C.V. 21-22.
4. Rex, A. (2011). Grundlagen der Physik. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Universitätsphysik mit moderner Physik. 14^th. Ed. Volume1. 50 - 53.
6. Serway, R., Jewett, J. (2008). Physik für Wissenschaft und Technik. Band 1. 7^ma. Auflage. Mexiko. Cengage Learning Editors. 23-25.
7. Serway, R., Vulle, C. (2011). Grundlagen der Physik. 9^{n / A} Ed. Lernen einbinden. 43 - 55.
8. Wilson, J. (2011). Physik 10. Pearson Education. 133 - 149.