
Binomialsatz Beweis und Beispiele
Das Binomialsatz ist eine Gleichung, die uns sagt, wie man einen Ausdruck der Form (a + b) entwickelt.n für eine natürliche Zahl n. Ein Binom ist nichts anderes als die Summe zweier Elemente wie (a + b). Es erlaubt uns auch, einen Begriff zu kennen, der durch a gegeben istkbn-k Was ist der Koeffizient, der damit einhergeht?.
Dieser Satz wird allgemein dem englischen Erfinder, Physiker und Mathematiker Sir Isaac Newton zugeschrieben; Es wurden jedoch verschiedene Aufzeichnungen gefunden, die darauf hinweisen, dass seine Existenz bereits im Nahen Osten um das Jahr 1000 bekannt war.

Artikelverzeichnis
- 1 Kombinatorische Zahlen
- 2 Demo
- 3 Beispiele
- 3.1 Identität 1
- 3.2 Identität 2
- 4 Eine weitere Demonstration
- 4.1 Beweis durch Induktion
- 5 Kuriositäten
- 6 Referenzen
Kombinatorische Zahlen
Der Binomialsatz sagt uns mathematisch Folgendes:
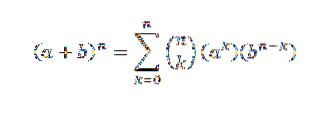
In diesem Ausdruck sind a und b reelle Zahlen und n ist eine natürliche Zahl.
Bevor wir die Demo geben, schauen wir uns einige grundlegende Konzepte an, die notwendig sind.
Die kombinatorische Zahl oder Kombinationen von n in k wird wie folgt ausgedrückt:
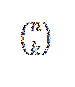
Diese Form drückt den Wert aus, wie viele Teilmengen mit k Elementen aus einer Menge von n Elementen ausgewählt werden können. Sein algebraischer Ausdruck ist gegeben durch:
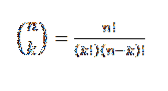
Schauen wir uns ein Beispiel an: Nehmen wir an, wir haben eine Gruppe von sieben Bällen, von denen zwei rot und der Rest blau sind..
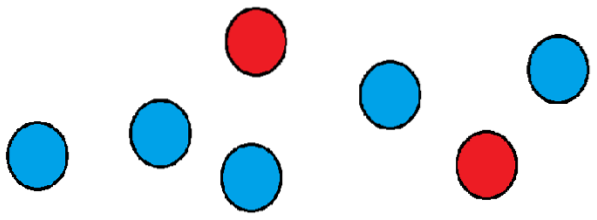
Wir möchten wissen, auf wie viele Arten wir sie hintereinander anordnen können. Eine Möglichkeit könnte darin bestehen, die beiden Rottöne an der ersten und zweiten Position und den Rest der Bälle an den verbleibenden Positionen zu platzieren..
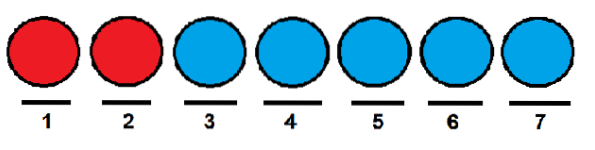
Ähnlich wie im vorherigen Fall könnten wir den roten Kugeln die erste bzw. letzte Position geben und die anderen mit blauen Kugeln besetzen.
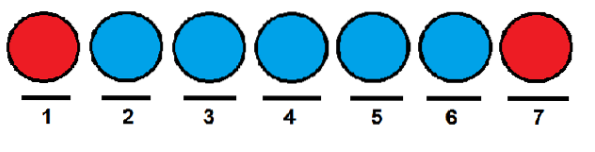
Eine effiziente Methode, um zu zählen, wie viele Arten wir die Kugeln in einer Reihe anordnen können, ist die Verwendung kombinatorischer Zahlen. Wir können jede Position als ein Element der folgenden Menge sehen:
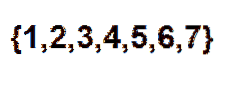
Dann bleibt nur noch eine Teilmenge von zwei Elementen zu wählen, wobei jedes dieser Elemente die Position darstellt, die die roten Kugeln einnehmen werden. Wir können diese Wahl gemäß der Beziehung treffen, die gegeben ist durch:
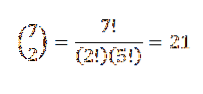
Auf diese Weise haben wir 21 Möglichkeiten, diese Bälle zu bestellen.
Die allgemeine Idee dieses Beispiels wird sehr nützlich sein, um den Binomialsatz zu beweisen. Schauen wir uns einen bestimmten Fall an: Wenn n = 4 ist, haben wir (a + b)4, Das ist nichts weiter als:
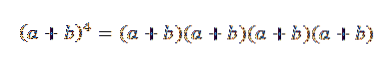
Wenn wir dieses Produkt entwickeln, bleibt uns die Summe der Terme übrig, die durch Multiplikation eines Elements von jedem der vier Faktoren (a + b) erhalten werden. Wir werden also Begriffe haben, die die Form haben:
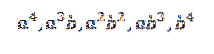
Wenn wir den Begriff aus dem Formular a erhalten wollten4, Multiplizieren Sie einfach wie folgt:
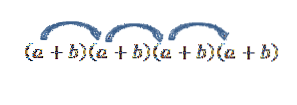
Beachten Sie, dass es nur einen Weg gibt, dieses Element zu erhalten. aber was passiert, wenn wir jetzt nach dem Begriff der Form a suchen?zweibzwei? Da "a" und "b" reelle Zahlen sind und daher das kommutative Gesetz gültig ist, besteht eine Möglichkeit, diesen Begriff zu erhalten, darin, mit den durch die Pfeile angegebenen Elementen zu multiplizieren.
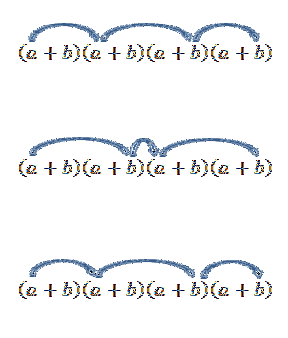
Das Ausführen all dieser Operationen ist normalerweise etwas mühsam, aber wenn wir den Begriff "a" als eine Kombination betrachten, bei der wir wissen möchten, auf wie viele Arten wir zwei "a" aus einer Reihe von vier Faktoren auswählen können, können wir die Idee aus dem verwenden vorheriges Beispiel. Wir haben also Folgendes:
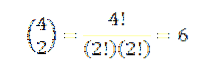
Somit wissen wir, dass in der endgültigen Erweiterung des Ausdrucks (a + b)4 wir werden genau 6a habenzweibzwei. Wenn Sie dieselbe Idee für die anderen Elemente verwenden, müssen Sie:
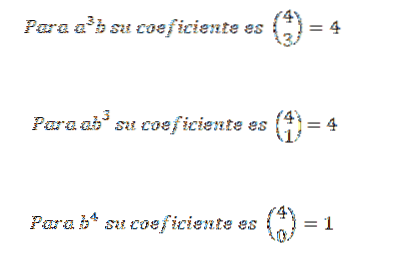
Dann fügen wir die zuvor erhaltenen Ausdrücke hinzu und wir haben das:
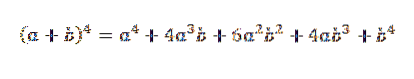
Es ist ein formaler Beweis für den allgemeinen Fall, in dem "n" eine natürliche Zahl ist.
Demonstration
Beachten Sie, dass die Begriffe, die bei der Entwicklung verbleiben (a + b)n Sie haben die Form akbn-k, wobei k = 0,1,…, n. Unter Verwendung der Idee des vorherigen Beispiels haben wir die Möglichkeit, "k" -Variablen "a" der "n" -Faktoren zu wählen:
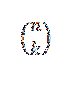
Auf diese Weise wählen wir automatisch n-k Variablen "b". Daraus folgt:
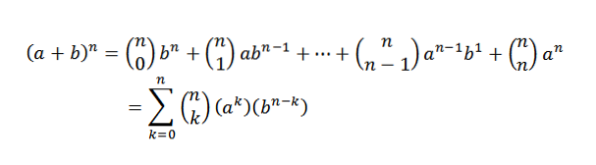
Beispiele
Betrachtet man (a + b)5, Was wäre Ihre Entwicklung??
Nach dem Binomialsatz haben wir:
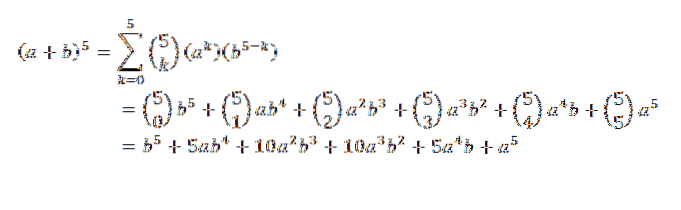
Der Binomialsatz ist sehr nützlich, wenn wir einen Ausdruck haben, in dem wir wissen wollen, wie hoch der Koeffizient eines bestimmten Terms ist, ohne die vollständige Erweiterung durchführen zu müssen. Als Beispiel können wir folgendes Unbekanntes nehmen: Was ist der Koeffizient von x?7Y.9 bei der Erweiterung von (x + y)16?
Nach dem Binomialsatz haben wir, dass der Koeffizient ist:
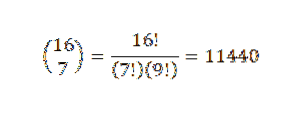
Ein anderes Beispiel wäre: Was ist der Koeffizient von x?5Y.8 in der Entwicklung von (3x-7y)13?
Zuerst schreiben wir den Ausdruck auf bequeme Weise um; das ist:
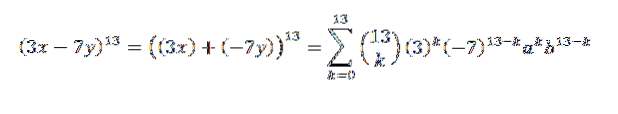
Dann haben wir unter Verwendung des Binomialsatzes, dass der gesuchte Koeffizient ist, wenn wir k = 5 haben
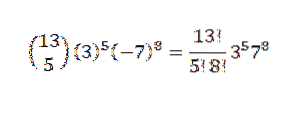
Ein weiteres Beispiel für die Verwendung dieses Theorems ist der Beweis einiger gemeinsamer Identitäten, wie die, die wir unten erwähnen werden.
Identität 1
Wenn "n" eine natürliche Zahl ist, haben wir:
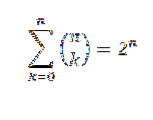
Für den Beweis verwenden wir den Binomialsatz, wobei sowohl "a" als auch "b" den Wert 1 annehmen. Dann haben wir:
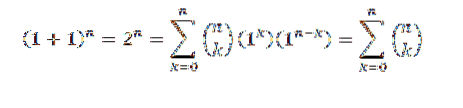
Auf diese Weise haben wir die erste Identität bewiesen.
Identität 2
Wenn "n" eine natürliche Zahl ist, dann
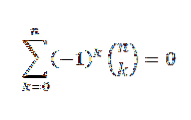
Nach dem Binomialsatz haben wir:
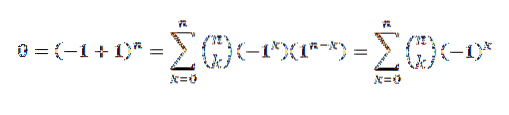
Eine weitere Demonstration
Wir können einen anderen Beweis für den Binomialsatz unter Verwendung der induktiven Methode und der Identität von Pascal liefern, der uns sagt, dass wenn „n“ und „k“ positive ganze Zahlen sind, die n ≥ k erfüllen, dann:
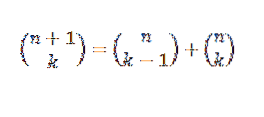
Induktionssicher
Lassen Sie uns zuerst sehen, dass die induktive Basis gilt. Wenn n = 1 ist, haben wir:
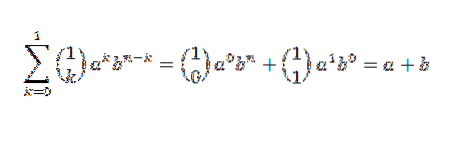
In der Tat sehen wir, dass es erfüllt ist. Nun sei n = j so, dass:
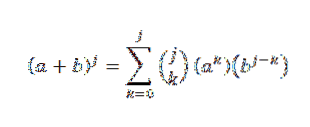
Wir wollen sehen, dass für n = j + 1 wahr ist, dass:
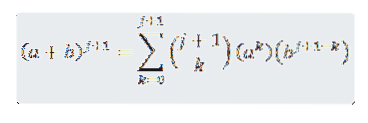
Also müssen wir:
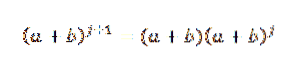
Durch die Hypothese wissen wir, dass:
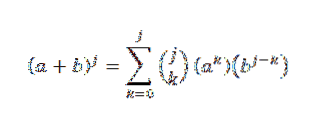
Verwenden Sie dann die Verteilungseigenschaft:
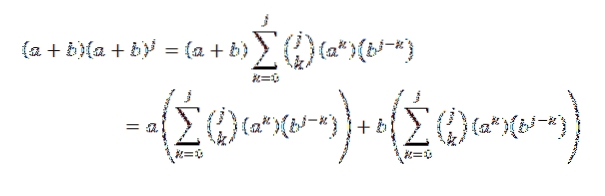
Anschließend haben wir bei der Entwicklung jeder der Summierungen:
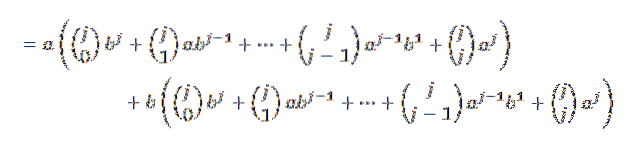
Wenn wir auf bequeme Weise gruppieren, haben wir Folgendes:
Mit der Identität von Pascal haben wir:
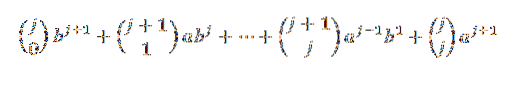
Beachten Sie abschließend Folgendes:
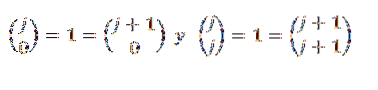
Wir sehen also, dass der Binomialsatz für alle "n" gilt, die zu den natürlichen Zahlen gehören, und damit endet der Beweis.
Kuriositäten
Die kombinatorische Zahl (nk) wird auch als Binomialkoeffizient bezeichnet, da genau der Koeffizient bei der Entwicklung des Binomials (a + b) auftritt.n.
Isaac Newton gab eine Verallgemeinerung dieses Theorems für den Fall, in dem der Exponent eine reelle Zahl ist; Dieser Satz ist als Newtons Binomialsatz bekannt.
Bereits in der Antike war dieses Ergebnis für den besonderen Fall bekannt, in dem n = 2 ist. Dieser Fall wird in der Elemente von Euklid.
Verweise
- Johnsonbaugh Richard. Diskrete Mathematik. PHH
- Kenneth.H. Rosen. Diskrete Mathematik und ihre Anwendungen. S. A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Seymour Lipschutz Ph.D & Marc Lipson. Diskrete Mathematik. McGRAW-HILL.
- Ralph P. Grimaldi. Diskrete Mathematik und Kombinatorik. Addison-Wesley Iberoamericana
- Verde Star Luis… Diskrete und kombinatorische Mathematik.Anthropos



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.