
Satz von Bozen Erklärung, Anwendungen und Übungen
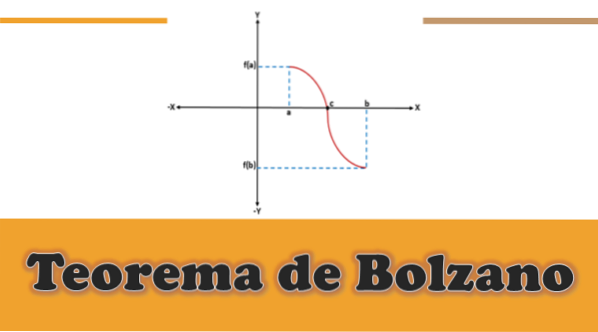
Das Satz von Bozen stellt fest, dass, wenn eine Funktion an allen Punkten eines geschlossenen Intervalls [a, b] stetig ist und das Bild von „a“ und „b“ (unter der Funktion) entgegengesetzte Vorzeichen hat, es mindestens eines gibt Punkt "C" im offenen Intervall (a, b), so dass die in "c" ausgewertete Funktion gleich 0 ist.
Dieser Satz wurde 1850 vom Philosophen, Theologen und Mathematiker Bernard Bozen formuliert. Der in der heutigen Tschechischen Republik geborene Wissenschaftler war einer der ersten Mathematiker in der Geschichte, der einen formalen Beweis für die Eigenschaften kontinuierlicher Funktionen erbrachte..
Artikelverzeichnis
- 1 Erklärung
- 2 Demo
- 3 Wofür ist es??
- 4 Gelöste Übungen
- 4.1 Übung 1
- 4.2 Übung 2
- 5 Referenzen
Erläuterung
Der Satz von Bozen ist auch als Zwischenwertsatz bekannt, der bei der Bestimmung bestimmter Werte, insbesondere Nullen, bestimmter reeller Funktionen einer reellen Variablen hilft.
In einer gegebenen Funktion setzt sich f (x) fort - das heißt, dass f (a) und f (b) durch eine Kurve verbunden sind -, wobei f (a) unterhalb der x-Achse liegt (es ist negativ) und f ( b) Über der x-Achse (es ist positiv) oder umgekehrt gibt es grafisch einen Grenzpunkt auf der x-Achse, der einen Zwischenwert "c" darstellt, der zwischen "a" und "a" liegt "B" und der Wert von f (c) ist gleich 0.
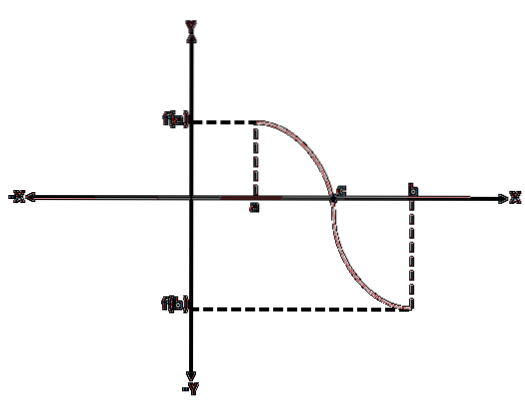
Durch grafische Analyse des Bozenschen Theorems kann gesehen werden, dass für jede stetige Funktion f in einem Intervall [a, b] definiert ist, wobei f (a)* *Wenn f (b) kleiner als 0 ist, gibt es innerhalb des Intervalls (a, b) mindestens eine Wurzel "c" dieser Funktion..
Dieser Satz legt nicht die Anzahl der Punkte in diesem offenen Intervall fest, sondern besagt nur, dass es mindestens 1 Punkt gibt.
Demonstration
Um den Satz von Bozen zu beweisen, wird ohne Verlust der Allgemeinheit angenommen, dass f (a) < 0 y f(b) > 0; Somit kann es viele Werte zwischen "a" und "b" geben, für die f (x) = 0 ist, aber es muss nur gezeigt werden, dass es einen gibt.
Wir beginnen mit der Auswertung von f im Mittelpunkt (a + b) / 2. Wenn f ((a + b) / 2) = 0 ist, endet der Beweis hier; andernfalls ist f ((a + b) / 2) positiv oder negativ.
Eine der Hälften des Intervalls [a, b] wird so gewählt, dass die Vorzeichen der an den Extremen bewerteten Funktion unterschiedlich sind. Dieses neue Intervall ist [a1, b1].
Wenn nun f, das im Mittelpunkt von [a1, b1] ausgewertet wird, nicht Null ist, wird dieselbe Operation wie zuvor ausgeführt; Das heißt, es wird eine Hälfte dieses Intervalls gewählt, die die Bedingung der Zeichen erfüllt. Dieses neue Intervall sei [a2, b2].
Wenn Sie mit diesem Vorgang fortfahren, haben Sie zwei Sequenzen an und bn, so dass:
an nimmt zu und bn nimmt ab:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Wenn die Länge jedes Intervalls [ai, bi] berechnet wird, haben wir:
b1-a1 = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Daher ist die Grenze, da n gegen unendlich von (bn-an) tendiert, gleich 0.
Wenn wir verwenden, dass an zunimmt und begrenzt wird und bn abnimmt und begrenzt wird, haben wir, dass es einen Wert "c" gibt, so dass:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Die Grenze von an ist "c" und die Grenze von bn ist auch "c". Daher gibt es bei jedem δ> 0 immer ein "n", so dass das Intervall [an, bn] innerhalb des Intervalls (c-δ, c + δ) enthalten ist..
Nun muss gezeigt werden, dass f (c) = 0 ist.
Wenn f (c)> 0 ist, existiert, da f stetig ist, ein & epsi;> 0, so dass f über das gesamte Intervall positiv ist (c - & epsi;, c + & epsi;). Wie oben erwähnt, gibt es jedoch einen Wert "n", so dass f das Vorzeichen in [an, bn] ändert und außerdem [an, bn] in (c-ε, c + ε) enthalten ist, was a ist Widerspruch.
Wenn f (c) < 0, entonces como f es continua, existe un ε >0, so dass f während des gesamten Intervalls negativ ist (c - & epsi;, c + & epsi;); aber es gibt einen Wert "n", so dass f das Vorzeichen in [an, bn] ändert. Es stellt sich heraus, dass [an, bn] in (c-ε, c + ε) enthalten ist, was ebenfalls ein Widerspruch ist.
Daher ist f (c) = 0 und das wollten wir zeigen.
Wofür ist das?
Aus seiner grafischen Interpretation wird der Satz von Bozen verwendet, um Wurzeln oder Nullen in einer stetigen Funktion durch Halbierung (Approximation) zu finden, eine inkrementelle Suchmethode, bei der die Intervalle immer durch 2 geteilt werden.
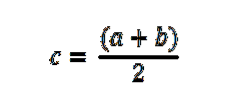
Dann wird ein Intervall [a, c] oder [c, b] genommen, in dem der Vorzeichenwechsel auftritt, und der Vorgang wird wiederholt, bis das Intervall immer kleiner wird, um näher an den gewünschten Wert heranzukommen; das heißt, auf den Wert, den die Funktion 0 macht.
Zusammenfassend werden die folgenden Schritte ausgeführt, um den Satz von Bozen anzuwenden und damit die Wurzeln zu finden, die Nullen einer Funktion zu begrenzen oder eine Lösung für eine Gleichung zu geben:
- Es wird überprüft, ob f eine stetige Funktion des Intervalls [a, b] ist..
- Wenn das Intervall nicht angegeben ist, muss man dort finden, wo die Funktion stetig ist.
- Es wird überprüft, ob die Extreme des Intervalls bei Auswertung bei f entgegengesetzte Vorzeichen ergeben.
- Wenn keine entgegengesetzten Vorzeichen erhalten werden, muss das Intervall unter Verwendung des Mittelpunkts in zwei Teilintervalle unterteilt werden.
- Bewerten Sie die Funktion im Mittelpunkt und stellen Sie sicher, dass die Bozen-Hypothese erfüllt ist, wobei f (a) * * f (b) < 0.
- Abhängig vom Vorzeichen (positiv oder negativ) des gefundenen Werts wird der Vorgang mit einem neuen Teilintervall wiederholt, bis die oben genannte Hypothese erfüllt ist..
Gelöste Übungen
Übung 1
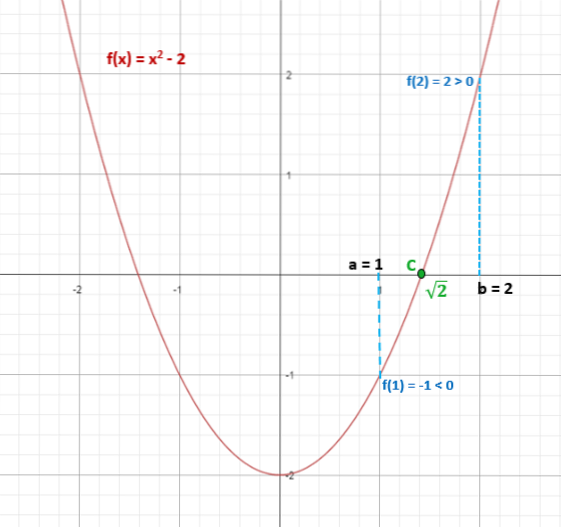
Bestimmen Sie, ob die Funktion f (x) = x istzwei - 2, hat mindestens eine echte Lösung im Intervall [1,2].
Lösung
Wir haben die Funktion f (x) = xzwei - 2. Da es ein Polynom ist, bedeutet es, dass es in jedem Intervall stetig ist.
Es wird gefragt, ob es im Intervall eine echte Lösung gibt [1, 2], daher ist es jetzt nur noch erforderlich, die Extreme des Intervalls in der Funktion zu ersetzen, um das Vorzeichen dieser zu kennen und um zu wissen, ob sie die Bedingung erfüllen anders zu sein:
f (x) = xzwei - zwei
f (1) = 1zwei - 2 = -1 (negativ)
f (2) = 2zwei - 2 = 2 (positiv)
Daher ist das Vorzeichen von f (1) ≠ das Vorzeichen von f (2).
Dies stellt sicher, dass es mindestens einen Punkt "c" gibt, der zu dem Intervall [1,2] gehört, in dem f (c) = 0 ist.
In diesem Fall kann der Wert von "c" leicht wie folgt berechnet werden:
xzwei - 2 = 0
x = ± √2.
Somit gehört √2 ≈ 1,4 zum Intervall [1,2] und erfüllt f (√2) = 0.
Übung 2
Zeigen Sie, dass die Gleichung x5 + x + 1 = 0 hat mindestens eine echte Lösung.
Lösung
Beachten wir zunächst, dass f (x) = x ist5 + x + 1 ist eine Polynomfunktion, was bedeutet, dass sie auf allen reellen Zahlen stetig ist.
In diesem Fall wird kein Intervall angegeben, daher müssen Werte intuitiv ausgewählt werden, vorzugsweise nahe 0, um die Funktion zu bewerten und die Vorzeichenänderungen zu finden:
Wenn Sie das Intervall [0, 1] verwenden, müssen Sie:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Da es keinen Vorzeichenwechsel gibt, wird der Vorgang mit einem weiteren Intervall wiederholt.
Wenn Sie das Intervall [-1, 0] verwenden, müssen Sie:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
In diesem Intervall gibt es einen Vorzeichenwechsel: Vorzeichen von f (-1) ≠ Vorzeichen von f (0), was bedeutet, dass die Funktion f (x) = x ist5 + x + 1 hat mindestens eine reelle Wurzel "c" im Intervall [-1, 0], so dass f (c) = 0. Mit anderen Worten, es ist wahr, dass x5 + x + 1 = 0 hat eine echte Lösung im Intervall [-1,0].
Verweise
- Bronshtein I, S. K. (1988). Mathematikhandbuch für Ingenieure und Studenten… Editorial MIR.
- George, A. (1994). Mathematik und Geist. Oxford University Press.
- Ilín V, P. E. (1991). Mathematische Analyse. In drei Bänden ...
- Jesús Gómez, F. G. (2003). Sekundarschullehrer. Band II. WÜTEND.
- Mateos, M. L. (2013). Grundlegende Eigenschaften der Analyse in R. Editores, 20. Dezember.
- Piskunov, N. (1980). Differential- und Integralrechnung ...
- Sydsaeter K, H. P. (2005). Mathematik für die Wirtschaftsanalyse. Felix Varela.
- William H. Barker, R. H. (s.f.). Kontinuierliche Symmetrie: Von Euklid zu Klein. American Mathematical Soc.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.