
Erklärung des Bayes-Theorems, Anwendungen, Übungen
Das Bayes-Theorem ist eine Prozedur, die es uns ermöglicht, die bedingte Wahrscheinlichkeit eines zufälligen Ereignisses A bei gegebenem B in Form der Wahrscheinlichkeitsverteilung von Ereignis B bei gegebenem A und der Wahrscheinlichkeitsverteilung von nur A auszudrücken.
Dieser Satz ist sehr nützlich, da wir dank ihm die Wahrscheinlichkeit, dass ein Ereignis A auftritt, in dem Wissen, dass B aufgetreten ist, mit der Wahrscheinlichkeit in Beziehung setzen können, dass das Gegenteil eintritt, dh dass B bei A auftritt.
Der Satz von Bayes war ein Silbersatz von Reverend Thomas Bayes, einem englischen Theologen des 18. Jahrhunderts, der auch Mathematiker war. Er war Autor mehrerer theologischer Werke, ist aber derzeit für einige mathematische Abhandlungen bekannt, von denen das bereits erwähnte Bayes-Theorem als Hauptergebnis hervorsticht.
Bayes beschäftigte sich mit diesem Theorem in einer 1763 veröffentlichten Arbeit mit dem Titel "Ein Essay zur Lösung eines Problems in der Doctrine of Chances", zu der eine große Anzahl entwickelt wurde. Studien mit Anwendungen in verschiedenen Wissensgebieten.
Artikelverzeichnis
- 1 Erklärung
- 2 Anwendungen des Bayes-Theorems
- 2.1 Gelöste Übungen
- 3 Referenzen
Erläuterung
Zum besseren Verständnis dieses Theorems sind zunächst einige Grundbegriffe der Wahrscheinlichkeitstheorie erforderlich, insbesondere der Multiplikationssatz für die bedingte Wahrscheinlichkeit, der dies besagt
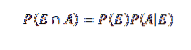
Für E und A beliebige Ereignisse eines Probenraums S..
Und die Definition von Partitionen, die uns sagt, dass wenn wir A haben1 ,ZUzwei,…, TOn Ereignisse eines Probenraums S bilden diese eine Partition von S, wenn das A.ich schließen sich gegenseitig aus und ihre Vereinigung ist S..
Vor diesem Hintergrund sei B ein weiteres Ereignis. Wir können also B als sehen
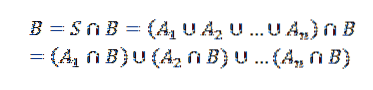
Wo die A.ich mit B geschnitten sind sich gegenseitig ausschließende Ereignisse.
Und in der Folge,
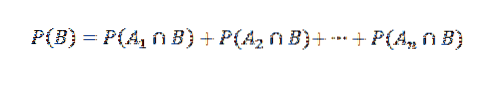
Dann wird der Multiplikationssatz angewendet
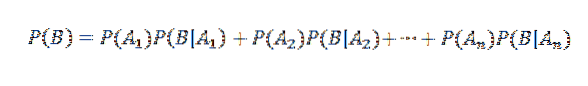
Andererseits ist die bedingte Wahrscheinlichkeit von Ai bei gegebenem B definiert durch
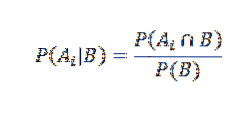
Wenn wir es angemessen ersetzen, haben wir das für jedes i
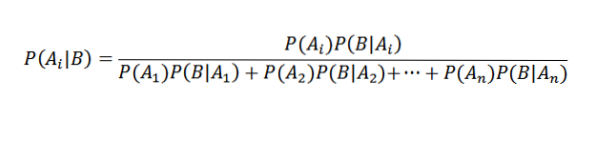
Anwendungen des Bayes'schen Theorems
Dank dieses Ergebnisses ist es Forschungsgruppen und verschiedenen Unternehmen gelungen, wissensbasierte Systeme zu verbessern..
Zum Beispiel kann bei der Untersuchung von Krankheiten das Bayes-Theorem helfen, die Wahrscheinlichkeit zu erkennen, dass eine Krankheit bei einer Gruppe von Menschen mit einem bestimmten Merkmal gefunden wird, wobei die globalen Krankheitsraten und das Vorherrschen dieser Merkmale in beiden als Daten herangezogen werden gesunde und kranke Menschen.
Andererseits hat es in der Welt der Hochtechnologien große Unternehmen beeinflusst, die dank dieses Ergebnisses "wissensbasierte" Software entwickelt haben.
Als tägliches Beispiel haben wir den Microsoft Office-Assistenten. Das Bayes-Theorem hilft der Software, die vom Benutzer präsentierten Probleme zu bewerten und zu bestimmen, welche Ratschläge zu geben sind, und somit in der Lage zu sein, einen besseren Service gemäß den Gewohnheiten des Benutzers anzubieten.
Es sollte beachtet werden, dass diese Formel bis vor kurzem ignoriert wurde, was hauptsächlich darauf zurückzuführen ist, dass dieses Ergebnis, als es vor 200 Jahren entwickelt wurde, für sie wenig praktischen Nutzen hatte. In unserer Zeit haben Wissenschaftler dank des großen technologischen Fortschritts Wege gefunden, dieses Ergebnis in die Praxis umzusetzen.
Gelöste Übungen
Übung 1
Eine Handyfirma hat zwei Maschinen A und B. 54% der produzierten Handys werden von Maschine A und der Rest von Maschine B hergestellt. Nicht alle produzierten Handys sind in gutem Zustand.
Der Anteil der von A hergestellten defekten Mobiltelefone beträgt 0,2 und von B 0,5. Wie hoch ist die Wahrscheinlichkeit, dass ein Handy aus dieser Fabrik defekt ist? Wie groß ist die Wahrscheinlichkeit, dass ein Mobiltelefon, wenn es weiß, dass es defekt ist, von Maschine A stammt??
Lösung
Hier haben Sie ein Experiment, das in zwei Teilen durchgeführt wird; Im ersten Teil treten die Ereignisse auf:
A: Zelle hergestellt von Maschine A..
B: Zelle hergestellt von Maschine B..
Da Maschine A 54% der Mobiltelefone produziert und der Rest von Maschine B produziert wird, folgt, dass Maschine B 46% der Handys produziert. Die Wahrscheinlichkeiten dieser Ereignisse sind angegeben, nämlich:
P (A) = 0,54.
P (B) = 0,46.
Die Ereignisse des zweiten Teils des Experiments sind:
D: Handy defekt.
E: nicht defektes Handy.
Wie in der Erklärung angegeben, hängen die Wahrscheinlichkeiten dieser Ereignisse vom im ersten Teil erzielten Ergebnis ab:
P (D | A) = 0,2.
P (D | B) = 0,5.
Mit diesen Werten können auch die Wahrscheinlichkeiten der Komplemente dieser Ereignisse bestimmt werden, dh:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Y.
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Jetzt kann Ereignis D wie folgt geschrieben werden:
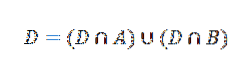
Verwenden des Multiplikationssatzes für bedingte Wahrscheinlichkeitsergebnisse:
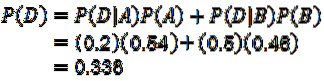
Womit die erste Frage beantwortet wird.
Jetzt müssen wir nur noch P (A | D) berechnen, für das der Bayes-Satz angewendet wird:
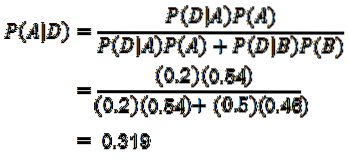
Dank des Bayes-Theorems kann festgestellt werden, dass die Wahrscheinlichkeit, dass ein Mobiltelefon von Maschine A hergestellt wurde, in dem Wissen, dass das Mobiltelefon defekt ist, 0,319 beträgt.
Übung 2
Drei Kisten enthalten schwarze und weiße Kugeln. Die Zusammensetzung von jedem von ihnen ist wie folgt: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
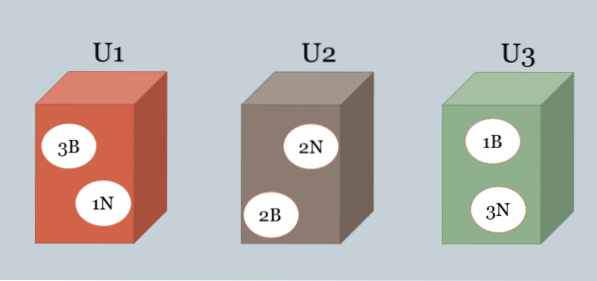
Eine der Boxen wird zufällig ausgewählt und eine Kugel wird zufällig gezogen, die sich als weiß herausstellt. Welche Box wurde am wahrscheinlichsten ausgewählt??
Lösung
Mit U1, U2 und U3 werden wir auch das ausgewählte Feld darstellen.
Diese Ereignisse stellen eine Partition von S dar und es wird verifiziert, dass P (U1) = P (U2) = P (U3) = 1/3 ist, da die Wahl der Box zufällig ist.
Wenn B = die gezogene Kugel ist weiß, haben wir P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Was wir erhalten möchten, ist die Wahrscheinlichkeit, dass der Ball aus der Schachtel Ui genommen wurde, in dem Wissen, dass der Ball weiß war, dh P (Ui | B), und zu sehen, welcher der drei Werte der höchste zu wissende war von welcher Box war höchstwahrscheinlich die Extraktion der weißen Kugel.
Anwendung des Bayes-Theorems auf das erste der Kästchen:
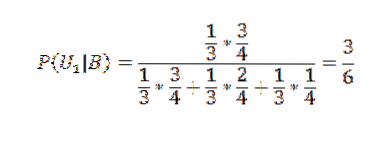
Und für die anderen beiden:
P (U2 | B) = 2/6 und P (U3 | B) = 1/6.
Dann ist die erste der Kisten diejenige mit der höchsten Wahrscheinlichkeit, für die Extraktion der weißen Kugel ausgewählt worden zu sein..
Verweise
- Kai Lai Chung. Elementare Proability-Theorie mit stochastischen Prozessen. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskrete Mathematik und ihre Anwendungen. S. A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Wahrscheinlichkeits- und statistische Anwendungen. S.A. MEXIKANISCHER ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Gelöste Probleme der diskreten Mathematik. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Theorie- und Wahrscheinlichkeitsprobleme. McGRAW-HILL.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.