
Volumenkörper der Umdrehung Volumen, Typen, gelöste Übungen
Das fest der Revolution Es ist die dreidimensionale Figur, die durch Drehen einer ebenen Fläche um die axiale Achse oder Rotationsachse erzeugt wird. Abbildung 1 zeigt eine Animation eines auf diese Weise erzeugten Rotationskörpers.
Ein weiteres sehr einfach zu visualisierendes Beispiel besteht darin, einen rechten Kreiszylinder zu erzeugen, der ein Rechteck mit der Höhe oder Länge h und dem Radius r um die positive x-Achse dreht (Abbildung 2). Um sein Volumen zu finden, gibt es eine bekannte Formel:
V = Grundfläche x Höhe
Andere Rotationskörper sind die Kugel, der rechte Kreiskegel und verschiedene Figuren, abhängig von der rotierten Oberfläche und natürlich der ausgewählten Achse..
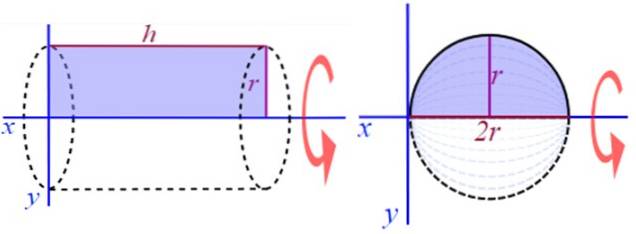
Zum Beispiel ergibt das Drehen des Halbkreises um eine Linie parallel zum Durchmesser einen Festkörper mit hohler Umdrehung.
Für den Zylinder, den Kegel, die Kugel, sowohl massiv als auch hohl, gibt es Formeln, um das Volumen zu finden, das vom Radius und der Höhe abhängt. Wenn sie jedoch von anderen Oberflächen erzeugt werden, wird das Volumen durch bestimmte Integrale berechnet.
Artikelverzeichnis
- 1 Arten von Rotationsfeststoffen
- 1.1 Kugel
- 1.2 Kegel
- 1.3 Zylinder
- 1.4 Toroid
- 2 Methoden zur Berechnung des Volumens eines Rotationskörpers
- 2.1 Scheiben- oder Unterlegscheibenmethode
- 2.2 Schichtmethode
- 3 Übung gelöst
- 4 Referenzen
Arten von Rotationsfeststoffen
Festkörper der Umdrehung können nach der Kurve klassifiziert werden, die sie erzeugt:
Kugel
Es reicht aus, einen Halbkreis um eine Achse zu drehen, die dem Durchmesser der Kugel mit dem Radius R entspricht. Das Volumen beträgt:
V.Kugel = (4/3) πR3
Kegel
Um einen Kegel mit der Höhe H und dem Radius R zu erhalten, ist die zu drehende Oberfläche ein rechtwinkliges Dreieck um die axiale Achse, die durch eines der Beine verläuft. Sein Volumen ist:
V.Kegel = (1/3) πHRzwei
Zylinder
Wenn wir ein Rechteck um eine axiale Achse drehen, die durch eine der Seiten verläuft, die die kurze oder die lange Seite sein kann, erhalten wir einen rechten Kreiszylinder mit dem Radius R und der Höhe H, dessen Volumen ist:
V.Zylinder = πRzweiH.
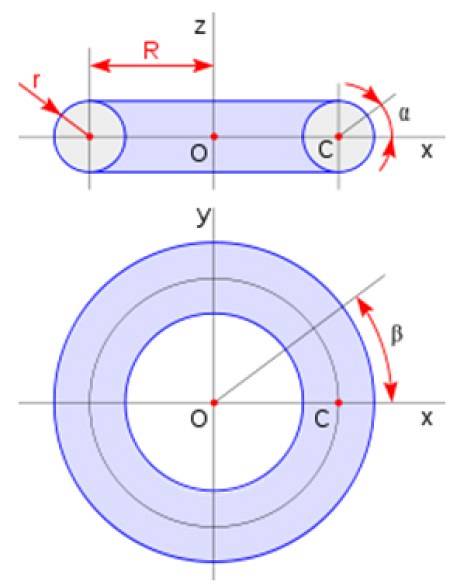
Toroid
Der Torus ist wie ein Donut geformt. Es wird erhalten, indem ein kreisförmiger Bereich um eine Linie in der Ebene gedreht wird, die den Kreis nicht schneidet. Sein Volumen ist gegeben durch:
V.Torus = 2πazweiR.
Wobei a der Radius des Querschnitts und R der Radius des Torus gemäß dem in der Abbildung dargestellten Schema ist:
Methoden zur Berechnung des Volumens eines Rotationskörpers
In der Integralrechnung sind diese beiden Methoden häufig:
-Scheiben und Unterlegscheiben
-Muscheln
Scheiben- oder Unterlegscheibenmethode
Beim Schneiden eines Rotationskörpers kann der Querschnitt eine Scheibe sein, wenn der Feststoff fest ist, oder eine Art Unterlegscheibe (eine Scheibe mit einem Loch in der Mitte), wenn es sich um einen hohlen Feststoff handelt..
Angenommen, ein planarer Bereich wird um die horizontale Achse gedreht. Aus diesem flachen Bereich nehmen wir ein kleines Rechteck mit der Breite Δx, das senkrecht um die axiale Achse gedreht wird.
Die Höhe des Rechtecks liegt zwischen der äußersten Kurve R (x) und der innersten Kurve r (x). Sie entsprechen dem Außenradius bzw. dem Innenradius..
Durch diese Drehung wird eine Unterlegscheibe mit dem Volumen ΔV erzeugt, gegeben durch:
ΔV = Vollvolumen - Lochvolumen (falls vorhanden)
Denken Sie daran, dass das Volumen eines rechten Kreiszylinders π beträgt. Radiozwei x Höhe haben wir:
ΔV = π [R.zwei(x) - rzwei(x)] Δx
Der Feststoff kann in eine Vielzahl von kleinen Volumenanteilen & Dgr; V unterteilt werden. Wenn wir sie alle hinzufügen, haben wir das volle Volumen.
Dazu lassen wir das Volumen ΔV gegen 0 tendieren, womit auch Δx sehr klein wird und ein Differential dx wird.
Wir haben also ein Integral:
V = ∫zub π [R.zwei(x) - rzwei(x)] dx
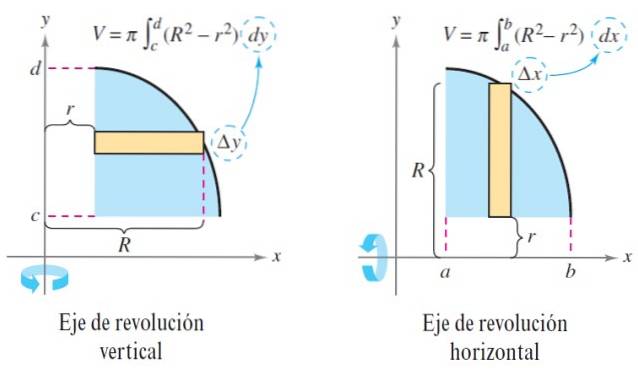
Wenn der Festkörper fest ist, dann ist die Funktion r (x) = 0, die Scheibe des Festkörpers, die erzeugt wird, ist eine Scheibe und das Volumen bleibt:
V = ∫zub πRzwei(x) dx
Wenn die Rotationsachse vertikal ist, haben die obigen Gleichungen die Form:
V = ∫zub π [R.zwei (y) - rzwei (y)] dy y V = ∫zub πRzwei(y) dy
Schichtmethode
Wie der Name schon sagt, besteht diese Methode darin, anzunehmen, dass der Festkörper aus Schichten unterschiedlicher Dicke besteht. Die Schicht ist ein dünnes Rohr, das aus der Drehung eines Rechtecks parallel zur Drehachse stammt.
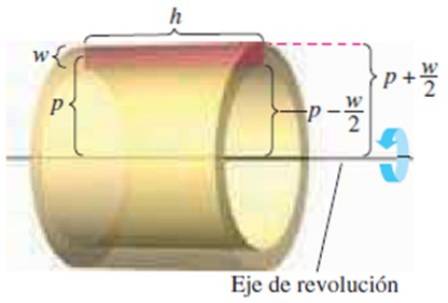
Wir haben folgende Abmessungen:
-Die Höhe des Rechtecks w
-Seine Länge h
-Der Abstand von der Mitte des Rechtecks zur Rotationsachse p
Wissen, dass das Volumen der Schicht ist Außenvolumen - Innenvolumen::
π (p + w / 2)zweih - π (p - w / 2)zweih
Durch die Entwicklung bemerkenswerter Produkte und die Vereinfachung erhalten Sie:
Schichtvolumen = 2π⋅p⋅w⋅h
Nehmen wir nun die Höhe w des Rechtecks Δy, wie in der folgenden Abbildung dargestellt:
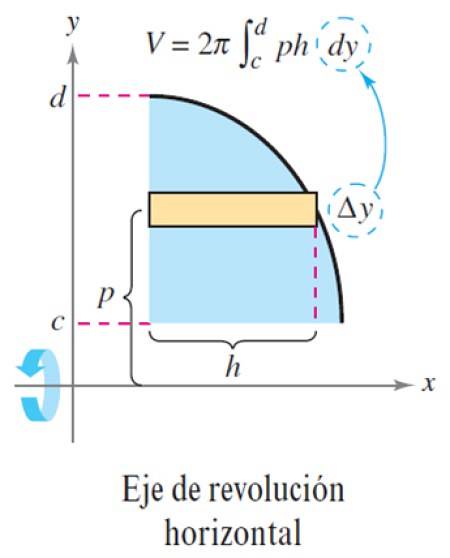
Damit ist das Volumen ΔV:
ΔV = 2π p x h x Δy
Und die Anzahl der Schichten machen n sehr groß ist, wird Δy zu einem Differential dy, bei dem das Gesamtvolumen das Integral ist:
V = ∫cd 2π p (y) h (y) dy
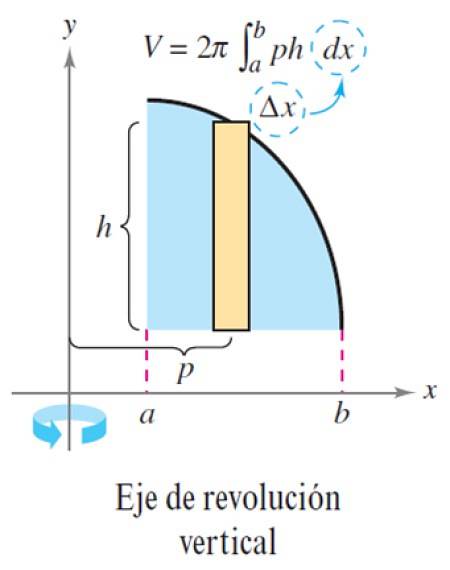
Das beschriebene Verfahren gilt ähnlich, wenn die Rotationsachse vertikal ist:
Übung gelöst
Finden Sie das Volumen, das durch die Drehung des ebenen Bereichs zwischen den Kurven erzeugt wird:
y = xzwei;; y = 0; x = 2
Um die y-Achse.
Lösung
-Als erstes müssen wir den Bereich grafisch darstellen, der den Rotationskörper erzeugt, und die Rotationsachse angeben. Wir haben es in der folgenden Grafik:
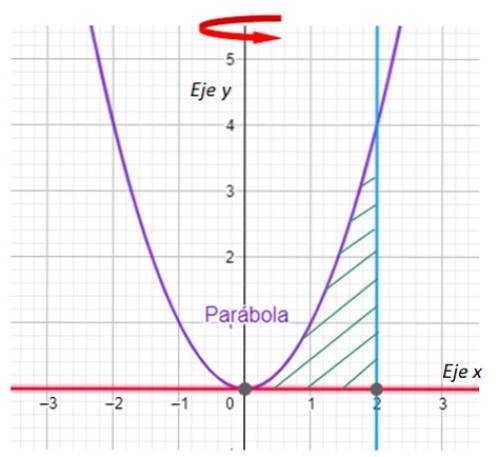
-Nun suchen wir nach den Schnittpunkten zwischen der Kurve y = xzwei und die Linie x = 2. Die Linie y = 0 ist ihrerseits nichts anderes als die x-Achse.
Aus dem Diagramm ist leicht ersichtlich, dass sich die Parabel und die Linie am Punkt (2,4) schneiden, was durch Einsetzen von x = 2 in y = x bestätigt wirdzwei.
-Dann wird eine der Methoden zur Berechnung des Volumens gewählt, beispielsweise die Schichtmethode mit vertikaler Rotationsachse:
V = ∫zub 2π p (x) h (x) dx
Schritt 1: Zeichnen Sie das Rechteck
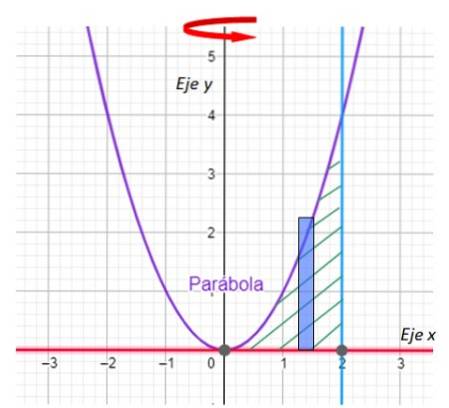
Wichtig: Bei der Schichtungsmethode verläuft die lange Seite des Rechtecks parallel zur Rotationsachse.
Schritt 2: Bestimmen Sie p (x)
Der Radius der Schicht ist x
Schritt 3: Bestimmen Sie h (x)
Die Höhe des Rechtecks wird durch die Parabel x bestimmtzwei.
Schritt 4: Legen Sie das Volumenintegral fest und lösen Sie es
Die Integrationsvariable ist x, die zwischen 0 und 2 variiert. Damit haben wir die Integrationsgrenzen. Ersetzen der Ausdrücke für p (x) und h (x)

Verweise
- Larson, R. 2010. Berechnung einer Variablen. 9 .. Auflage. Mcgraw Hügel.
- Purcell, E. 2007. Kalkül mit analytischer Geometrie. 9 .. Auflage. Pearson Ausbildung.
- Wikipedia. Fest der Revolution. Wiederhergestellt von: en.wikipedia.org.
- Wikipedia. Toroid Wiederhergestellt von: es.wikipedia.org.
- Wolfram MathWorld. Fest der Revolution. Wiederhergestellt von: mathworld.wolfram.com.

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.