
Magnetische Reluktanzeinheiten, Formeln, Berechnung, Beispiele
Das magnetische Reluktanz oder magnetischer Widerstand ist der Gegensatz, den ein Medium zum Durchgang des magnetischen Flusses darstellt: Je höher der Widerstand, desto schwieriger ist es, den magnetischen Fluss zu bestimmen. In einem Magnetkreis spielt der Widerstand die gleiche Rolle wie der elektrische Widerstand in einem Stromkreis.
Eine Spule, die von elektrischem Strom angetrieben wird, ist ein Beispiel für einen sehr einfachen Magnetkreis. Dank des Stroms wird ein magnetischer Fluss erzeugt, der von der geometrischen Anordnung der Spule und auch von der Intensität des durch sie fließenden Stroms abhängt..

Artikelverzeichnis
- 1 Formeln und Einheiten
- 2 Wie wird die magnetische Reluktanz berechnet??
- 3 Unterschied zum elektrischen Widerstand
- 4 Beispiele
- 4.1 Magnete
- 4.2 Auf einen rechteckigen Eisenkern gewickelte Spule
- 5 Übungen gelöst
- 5.1 - Übung 1
- 5.2 - Übung 2
- 6 Referenzen
Formeln und Einheiten
Bezeichnung des Magnetflusses als Φm, du hast:
Φm = N.i / (ℓc / μAc)
Wo:
-N ist die Anzahl der Windungen der Spule.
-Die Intensität des Stroms ist ich.
-ℓc repräsentiert die Länge der Schaltung.
-ZUc ist die Querschnittsfläche.
-μ ist die Permeabilität des Mediums.
Der Faktor im Nenner, der die Geometrie plus den Einfluss des Mediums kombiniert, ist genau die magnetische Reluktanz der Schaltung, eine skalare Größe, die mit dem Buchstaben ℜ bezeichnet wird, um sie vom elektrischen Widerstand zu unterscheiden. A) Ja:
ℜ = ℓc / μAc
Im Internationalen Einheitensystem (SI) wird ℜ als Umkehrung von Henry gemessen (multipliziert mit der Anzahl der Windungen N). Henry ist wiederum die Einheit für die magnetische Induktivität, was 1 Tesla (T) x Quadratmeter / Ampere entspricht. Deshalb:
1 STUNDE-1 = 1 A / T.zwei
Als 1 T.m.zwei = 1 Weber (Wb), Reluktanz wird auch in A / Wb ausgedrückt (Ampere / Weber oder häufiger Ampere-Turn / Weber).
Wie wird die magnetische Reluktanz berechnet??
Da die magnetische Reluktanz dieselbe Rolle spielt wie der elektrische Widerstand in einem Magnetkreis, ist es möglich, die Analogie für diese Schaltungen um ein Äquivalent des Ohmschen Gesetzes V = IR zu erweitern.
Obwohl es nicht richtig zirkuliert, ist der magnetische Fluss Φm tritt an die Stelle von Strom, während anstelle von Spannung V., definiert die magnetische Spannung oder magnetomotorische Kraft, analog zur elektromotorischen Kraft oder f.e.m. in Stromkreisen.
Die magnetomotorische Kraft ist für die Aufrechterhaltung des Magnetflusses verantwortlich. Abgekürzt f.m.m und wird als ℱ bezeichnet. Damit haben wir endlich eine Gleichung, die die drei Größen in Beziehung setzt:
ℱ = Φm . ℜ
Und mit der Gleichung vergleichen Φm = N.i / (ℓc / μAc), es wird geschlossen, dass::
ℱ = N.i.
Auf diese Weise kann die Reluktanz berechnet werden, indem die Geometrie des Schaltkreises und die Permeabilität des Mediums bekannt sind, oder auch der magnetische Fluss und die magnetische Spannung dank dieser letzten Gleichung, die genannt wird Hopkinsons Gesetz.
Unterschied zum elektrischen Widerstand
Die Gleichung für die magnetische Reluktanz ℜ = ℓc / μAc ist ähnlich wie R = L / σA für elektrischen Widerstand. In letzterem steht σ für die Leitfähigkeit des Materials, L für die Länge des Drahtes und A für seine Querschnittsfläche.
Diese drei Größen: σ, L und A sind konstant. Allerdings ist die Durchlässigkeit des Mediums μ, im allgemeinen ist es nicht konstant, so dass der magnetische Widerstand eines Stromkreises im Gegensatz zu seinem elektrischen Gleichnis auch nicht konstant ist.
Wenn sich das Medium ändert, beispielsweise beim Übergang von Luft zu Eisen oder umgekehrt, ändert sich die Permeabilität, was zu einer Änderung der Reluktanz führt. Und auch die magnetischen Materialien gehen durch Hysteresezyklen.
Dies bedeutet, dass das Anlegen eines externen Feldes bewirkt, dass das Material einen Teil des Magnetismus beibehält, selbst nachdem das Feld entfernt wurde..
Aus diesem Grund muss jedes Mal, wenn die magnetische Reluktanz berechnet wird, sorgfältig angegeben werden, an welchem Punkt im Zyklus sich das Material befindet, und somit seine Magnetisierung kennen..
Beispiele
Obwohl die Reluktanz stark von der Geometrie der Schaltung abhängt, hängt sie auch von der Permeabilität des Mediums ab. Je höher dieser Wert ist, desto geringer ist die Zurückhaltung. Dies ist der Fall bei ferromagnetischen Materialien. Luft hat andererseits eine geringe Permeabilität, daher ist ihre magnetische Reluktanz höher..
Magnete
Ein Magnet ist eine Wicklung mit einer Länge ℓ gemacht mit N Windungen, durch die ein elektrischer Strom I geleitet wird. Die Windungen sind im Allgemeinen kreisförmig gewickelt.
Innerhalb wird ein intensives und gleichmäßiges Magnetfeld erzeugt, während außerhalb des Feldes ungefähr Null wird..
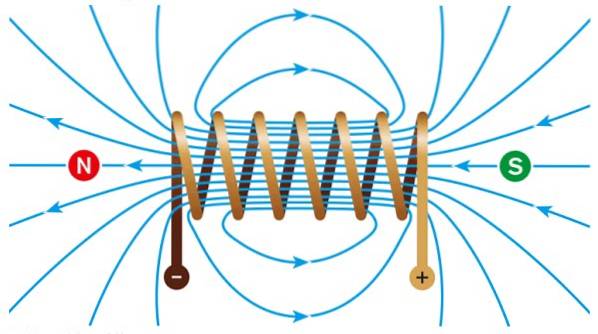
Wenn die Wicklung eine Kreisform hat, gibt es eine Torus. Im Inneren befindet sich möglicherweise Luft, aber wenn ein Eisenkern platziert wird, ist der Magnetfluss dank der hohen Permeabilität dieses Minerals viel höher.
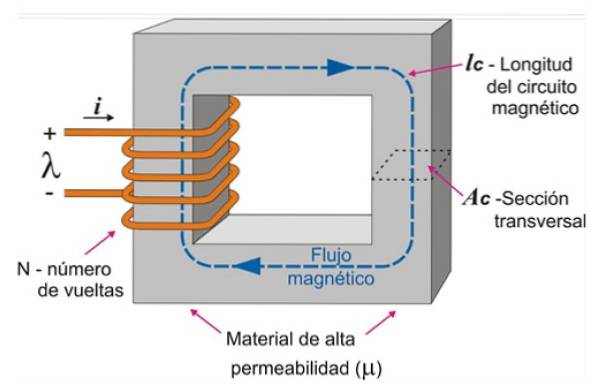
Spule auf einen rechteckigen Eisenkern gewickelt
Ein Magnetkreis kann aufgebaut werden, indem die Spule auf einen rechteckigen Eisenkern gewickelt wird. Auf diese Weise ist es möglich, einen intensiven Feldfluss innerhalb des Eisenkerns herzustellen, wenn ein Strom durch den Draht fließt, wie in Abbildung 3 gezeigt.
Die Reluktanz hängt von der Länge der Schaltung und der in der Figur angegebenen Querschnittsfläche ab. Die gezeigte Schaltung ist homogen, da der Kern aus einem einzigen Material besteht und der Querschnitt gleichmäßig bleibt..
Gelöste Übungen
- Übung 1
Ermitteln Sie die magnetische Reluktanz eines geradlinigen Solenoids mit 2000 Windungen und wissen Sie, dass bei einem Strom von 5 A ein magnetischer Fluss von 8 mWb erzeugt wird.
Lösung
Die Gleichung wird verwendet ℱ = N.i. zur Berechnung der magnetischen Spannung, da die Intensität des Stroms und die Anzahl der Windungen in der Spule zur Verfügung stehen. Es vervielfacht sich einfach:
ℱ = 2000 x 5 A = 10.000 Ampere-Umdrehung
Dann wird Gebrauch gemacht von ℱ = Φm . ℜ, Achten Sie darauf, den Magnetfluss in Weber auszudrücken (das Präfix "m" bedeutet "Milli", also wird es mit multipliziert 10 -3::
Φm = 8 x 10 -3 Wb
Jetzt wird die Zurückhaltung gelöscht und die Werte werden ersetzt:
ℜ = ℱ / Φm = 10.000 Ampere-Umdrehung / 8 x 10 -3 Wb = 1,25 · 106 Amp-Turn / Wb
- Übung 2
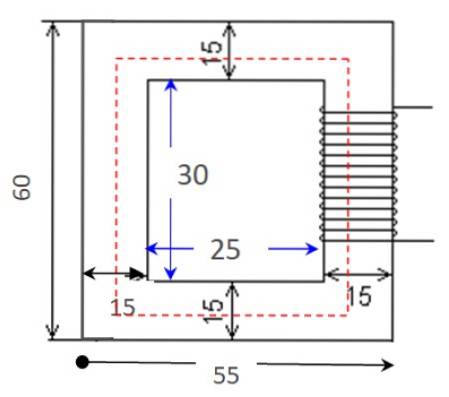
Berechnen Sie den magnetischen Widerstand der in der Abbildung gezeigten Schaltung mit den angegebenen Abmessungen in Zentimetern. Die Permeabilität des Kerns beträgt μ = 0,005655 Tm / A und die Querschnittsfläche ist konstant, 25 cmzwei.
Lösung
Wir werden die Formel anwenden:
ℜ = ℓc / μAc
Durchlässigkeit und Querschnittsfläche sind als Daten in der Erklärung verfügbar. Es bleibt die Länge der Schaltung zu ermitteln, die der Umfang des roten Rechtecks in der Abbildung ist.
Dazu wird die Länge einer horizontalen Seite gemittelt, wobei die größere Länge und die kürzere Länge addiert werden: (55 + 25 cm) / 2 = 40 cm. Gehen Sie dann für die vertikale Seite genauso vor: (60 + 30 cm) / 2 = 45 cm.
Schließlich werden die durchschnittlichen Längen der vier Seiten addiert:
ℓc = 2 x 40 cm + 2 x 45 cm = 170 cm
Subtrahieren Sie die Substitutionswerte in der Reluktanzformel, jedoch nicht bevor Sie die Länge und Fläche des Querschnitts - wie in der Anweisung angegeben - in SI-Einheiten ausgedrückt haben:
ℜ = 170 x 10 -zweim / (0,005655 Tm / A x 0,0025 mzwei) = 120.248 Ampere-Drehung / Wb
Verweise
- Alemán, M. Ferromagnetischer Kern. Wiederhergestellt von: youtube.com.
- Magnetkreis und Reluktanz. Wiederhergestellt von: mse.ndhu.edu.tw.
- Spinadel, E. 1982. Elektrische und magnetische Schaltkreise. Neue Bibliothek.
- Wikipedia. Magnetomotorische Kraft. Wiederhergestellt von: es.wikipedia.org.
- Wikipedia. Magnetische Reluktanz. Wiederhergestellt von: es.wikipedia.org.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.