
Konzept, Eigenschaften, Beispiele, Übungen von Bravais-Netzwerken
Das Bravais-Netze Sie sind die Menge von vierzehn dreidimensionalen Einheitszellen, in denen sich die Atome eines Kristalls befinden können. Diese Zellen bestehen aus einer dreidimensionalen Anordnung von Punkten, die eine Grundstruktur bilden, die sich periodisch in den drei Raumrichtungen wiederholt..
Der Ursprung dieser Bezeichnung für die kristallinen Grundstrukturen stammt aus dem Jahr 1850, als Auguste Bravais zeigte, dass es nur 14 mögliche dreidimensionale Grundeinheitszellen gibt.

Die Menge von 14 Bravais-Netzwerken ist entsprechend der Geometrie der Zellen in sieben Gruppen oder Strukturen unterteilt. Diese sieben Gruppen sind:
1- Kubisch
2- Tetragonal
3- Orthorhombisch
4- Trigonal-hexagonal
5- Monoklin
6- Triklinisch
7- Trigonal
Jede dieser Strukturen definiert eine Einheitszelle, wobei dies der kleinste Teil ist, der die geometrische Anordnung der Atome im Kristall beibehält..
Artikelverzeichnis
- 1 Eigenschaften von Bravais-Netzwerken
- 1.1 Kubische Netzwerke
- 2 Beispiele
- 2.1 - Eisen
- 2.2 - Kupfer
- 2.3 - Edelsteine
- 2.4 Topas
- 3 Gelöste Übungen
- 3.1 Übung 1
- 3.2 Übung 2
- 3.3 Übung 3
- 4 Referenzen
Eigenschaften von Bravais-Netzwerken
Die vierzehn Bravais-Netzwerke sind, wie oben erwähnt, in sieben Gruppen unterteilt. Aber jede dieser Gruppen hat ihre Einheitszellen mit ihren charakteristischen Parametern, die sind:
1- Der Netzwerkparameter (a, b, c)
2- Anzahl der Atome pro Zelle
3- Beziehung zwischen Netzwerkparameter und Atomradius
4- Koordinationsnummer
5- Verpackungsfaktor
6- Zwischenräume
7- Durch Translationen entlang der Vektoren a, b, c wird die Kristallstruktur wiederholt.
Kubische Netzwerke
Es besteht aus dem einfachen kubischen oder kubischen Netzwerk P, dem flächenzentrierten kubischen Netzwerk oder kubischen Netzwerk F und dem körperzentrierten kubischen Netzwerk oder kubischen Netzwerk I..
Alle kubischen Netzwerke haben alle drei Netzwerkparameter entsprechend den x-, y-, z-Richtungen des gleichen Wertes:
a = b = c
Kubisches Netzwerk P.
Es ist zu beachten, dass Atome durch Kugeln dargestellt werden, deren Zentren an den Eckpunkten der kubischen Einheitszelle P liegen.
Im Falle des kubischen Gitters P ist die Anzahl der Atome pro Zelle ist 1, weil sich an jedem Scheitelpunkt nur ein Achtel des Atoms innerhalb der Einheitszelle befindet, also 8 * ⅛ = 1.
Das Koordinationsnummer gibt die Anzahl der Atome an, die nahe Nachbarn im Kristallgitter sind. Im Fall des kubischen Gitters P beträgt die Koordinationszahl 6.
Kubisches Netzwerk I.
In dieser Art von Netzwerk befindet sich zusätzlich zu den Atomen an den Eckpunkten des Würfels ein Atom in der Mitte des Würfels. Also die Anzahl der Atome pro Zelle Einheit im kubischen Gitter P ist 2 Atome.

Kubisches Netzwerk F.
Es ist das kubische Gitter, das zusätzlich zu den Atomen in den Eckpunkten ein Atom in der Mitte der Fläche jedes Würfels hat. Das Anzahl der Atome pro Zelle ist 4, da jedes der sechs Atome des Gesichts die Hälfte in der Zelle hat, dh 6 * ½ = 3 plus 8 * ⅛ = 1 an den Eckpunkten.

Sechseckiges Netz
In diesem Fall ist die Einheitszelle ein gerades Prisma mit einer hexagonalen Basis. Hexagonale Netzwerke haben alle drei Netzwerkparameter entsprechend die folgende Beziehung erfüllen:
a = b ≠ c
Der Winkel zwischen Vektor a und b beträgt 120 °, wie in der Abbildung gezeigt. Während zwischen den Vektoren a und c sowie zwischen b und c rechte Winkel gebildet werden.

Das Anzahl der Atome pro Zelle wird wie folgt berechnet:
- In jeder der 2 Basen des hexagonalen Prismas befinden sich 6 Atome an den sechs Eckpunkten. Jedes dieser Atome nimmt ⅙ der Elementarzelle ein.
- In der Mitte jeder der 2 hexagonalen Basen befindet sich 1 Atom, das eine halbe Einheitszelle einnimmt.
- Auf den 6 Seitenflächen des hexagonalen Prismas befinden sich 3 Atome, die jeweils ⅔ der Einheitszelle einnehmen, und 3 Atome, die jeweils ⅓ des Einheitszellenvolumens einnehmen.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
Die Beziehung zwischen den Gitterparametern a und b mit dem Atomradius R unter der Annahme, dass alle Atome den gleichen Radius haben und in Kontakt stehen, ist:
a / R = b / R = 2
Beispiele
Metalle sind die Hauptbeispiele für kristalline Strukturen und auch die einfachsten, da sie im Allgemeinen nur aus einem Atomtyp bestehen. Es gibt aber auch andere nichtmetallische Verbindungen, die kristalline Strukturen bilden, wie Diamant, Quarz und viele andere..
- Das Bügeleisen
Eisen hat eine einzelne kubische Einheitszelle mit einem Gitter- oder Kantenparameter a = 0,297 nm. In 1 mm gibt es 3,48 x 10 ^ 6 Einheitszellen.
- Kupfer
Es hat eine flächenzentrierte kubische Kristallstruktur, die ausschließlich aus Kupferatomen besteht..
- Wertvolle Edelsteine
Edelsteine sind kristalline Strukturen aus im Wesentlichen derselben Verbindung, jedoch mit kleinen Anteilen an Verunreinigungen, die häufig für ihre Farbe verantwortlich sind..
Diamant
Es besteht ausschließlich aus Kohlenstoff und enthält keine Verunreinigungen, weshalb es farblos ist. Der Diamant hat kubische Kristallstruktur (isometrisch-hexoktaedrisch) und ist das härteste bekannte Material.
Quarz
Es besteht aus Siliciumdioxid, ist im Allgemeinen farblos oder weiß. Seine kristalline Struktur ist trigonal-trapezoedrisch.
Rubin
Es besteht aus Aluminiumoxid mit Chromverunreinigungen, die ihm seine charakteristische rote Farbe verleihen. Bilden Sie a hexagonales Kristallgitter.
Saphir
Es ist auch ein Kristall aus Aluminiumoxid, jedoch mit Verunreinigungen aus Titan und Eisen, die für seine blaue Farbe in verschiedenen Farbtönen verantwortlich sind. Wie der Rubin hat hexagonale Struktur.
Jade
Edelstein in der Regel grün gefärbt, hat monokline Struktur und besteht aus Eisen-Magnesium-Calcium-Silikat.
Topas
Es ist farblos mit einem orthorhombische Struktur Aluminiumfluorid-Hydroxid-Silikat.
Gelöste Übungen
Übung 1
Finden Sie die Beziehung zwischen dem Gitterparameter und dem Atomradius für ein kubisches Gitter F..
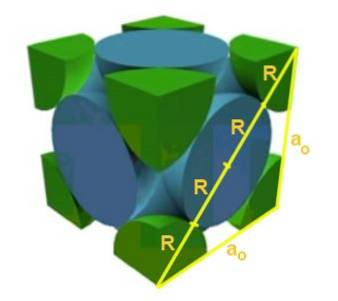
Lösung: Zunächst wird angenommen, dass die Atome als Kugeln mit dem gesamten Radius R in "Kontakt" miteinander dargestellt sind, wie in der Figur gezeigt. Es bildet sich ein rechtwinkliges Dreieck, in dem Folgendes zutrifft:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Daher lautet die Kanten-Radius-Beziehung:
a / R = 4 / √2
Übung 2
Finden Sie die Beziehung zwischen dem Gitterparameter und dem Atomradius für ein kubisches Gitter I (körperzentriert)..
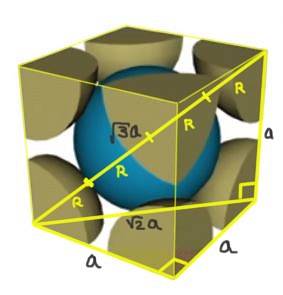
Lösung: Atome sollen als Kugeln mit dem gesamten Radius R in "Kontakt" miteinander dargestellt werden, wie in der Figur gezeigt.
Es werden zwei rechtwinklige Dreiecke gebildet, eines der Hypotenuse √2a und das andere der Hypotenuse √3a, wie mit dem Satz von Pythagoras bewiesen werden kann. Daraus folgt, dass die Beziehung zwischen dem Gitterparameter und dem Atomradius für ein kubisches Gitter I (im Körper zentriert) ist:
a / R = 4 / √3
Übung 3
Finden Sie den Packungsfaktor F für eine Einheitszelle einer kubischen Struktur F (flächenzentrierte Kubik), in der die Atome den Radius R haben und in "Kontakt" stehen..
Lösung: Der Packungsfaktor F ist definiert als der Quotient zwischen dem von den Atomen in der Einheitszelle eingenommenen Volumen und dem Volumen der Zelle:
F = V.Atome / V.Zelle
Wie oben gezeigt, beträgt die Anzahl der Atome pro Einheitszelle in einem flächenzentrierten kubischen Gitter 4, daher beträgt der Packungsfaktor:
F = 4 [4πR ^ 3/3] / [a ^ 3] =…
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Verweise
- Akademisches Ressourcenzentrum für Kristallstrukturen. [PDF]. Abgerufen am 24. Mai 2018 von: web.iit.edu
- Kristalle. Abgerufen am 26. Mai 2018 von :oughtco.com
- Pressebücher. 10.6 Gitterstrukturen in kristallinen Festkörpern. Abgerufen am 26. Mai 2018 von: opentextbc.ca
- Ming. (2015, 30. Juni). Typen Kristallstrukturen. Abgerufen am 26. Mai 2018 von: Crystalvisions-film.com
- Helmenstine, Anne Marie, Ph.D. (31. Januar 2018). Arten von
- Kittel Charles (2013) Festkörperphysik, Festkörperphysik (8. Auflage). Wiley.
- KHI. (2007). Kristalline Strukturen. Abgerufen am 26. Mai 2018 von: folk.ntnu.no
- Wikipedia. Bravais-Gitter. Wiederhergestellt von: en.wikipedia.com.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.