Das Schneidemodul beschreibt die Reaktion eines Materials auf das Aufbringen einer Scherspannung, die es verformt. Andere häufig verwendete Namen für den Schermodul sind der Schermodul, der Schermodul, die Querelastizität oder die Tangentialelastizität..
Wenn die Spannungen klein sind, sind die Verformungen gemäß dem Hookeschen Gesetz proportional zu ihnen, wobei der Schermodul die Proportionalitätskonstante ist. Deshalb:
Schubmodul = Schubspannung / Dehnung
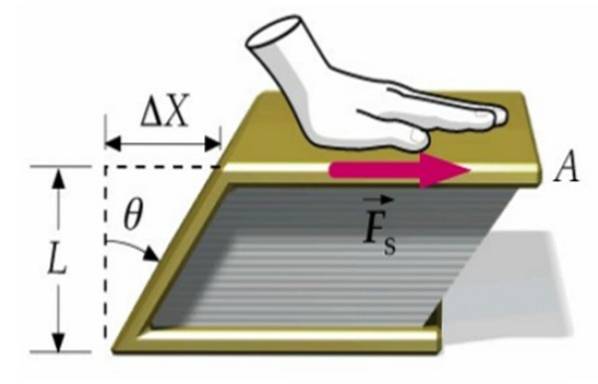
Angenommen, eine Kraft wird auf den Einband eines Buches ausgeübt, die andere auf der Oberfläche des Tisches. Auf diese Weise bewegt sich das Buch als Ganzes nicht, sondern verformt sich, wenn sich der obere Einband gegenüber dem unteren um den Betrag bewegt Δx.
Das Buch geht von einem rechteckigen Querschnitt zu einem parallelogrammförmigen Querschnitt über, wie wir im obigen Bild sehen.
Sein:
τ = F / A.
Die Scherspannung oder Spannung ist F. die Größe der ausgeübten Kraft und ZU der Bereich, auf den es wirkt.
Die verursachte Verformung ergibt sich aus dem Quotienten:
δ = Δx / L.
Daher ist der Schermodul, den wir als G bezeichnen werden:
Und da Δx / L keine Abmessungen hat, sind die Einheiten von G die gleichen wie die Scherspannung, die das Verhältnis von Kraft zu Fläche ist..
Im Internationalen Einheitensystem sind diese Einheiten Newton / Quadratmeter oder Pascal, abgekürzt Pa. In angelsächsischen Einheiten sind es Pfund / Quadratzoll, abgekürzt psi.
Artikelverzeichnis
Unter der Wirkung von Scherkräften wie den beschriebenen bieten die Objekte einen ähnlichen Widerstand wie das Buch, in dem die inneren Schichten gleiten. Diese Art der Verformung kann nur in festen Körpern auftreten, die eine ausreichende Steifigkeit aufweisen, um einer Verformung zu widerstehen..
Andererseits bieten Flüssigkeiten keinen solchen Widerstand, können jedoch Volumenverformungen erfahren.
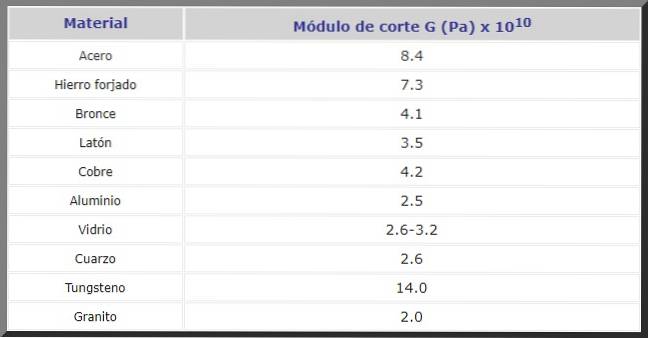
Nachfolgend finden Sie das Schneidmodul G in Pa für verschiedene Materialien, die häufig im Bauwesen und bei der Herstellung von Maschinen und Ersatzteilen aller Art verwendet werden:
Um den Wert des Schermoduls zu ermitteln, müssen Proben jedes Materials getestet und ihre Reaktion auf die Anwendung einer Scherspannung untersucht werden..
Die Probe ist ein Stab aus dem Material mit Radius R. und Länge L. bekannt, die an einem Ende befestigt ist, während das andere mit der Welle einer Riemenscheibe verbunden ist, die sich frei drehen kann.
Die Riemenscheibe ist mit einem Seil festgebunden, an dessen freiem Ende ein Gewicht aufgehängt ist, das eine Kraft ausübt F. auf der Stange durch das Seil. Und diese Kraft erzeugt wiederum einen Moment M. auf der Stange, die sich dann um einen kleinen Winkel θ dreht.
Ein Diagramm der Baugruppe ist in der folgenden Abbildung dargestellt:
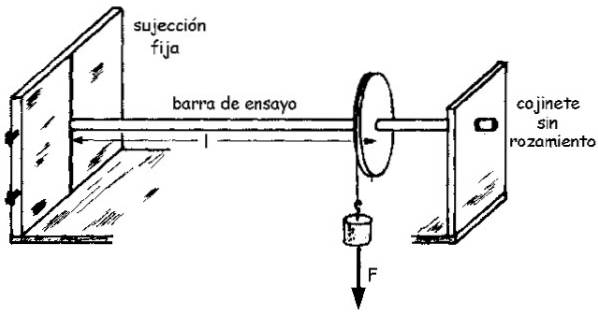
Die Größe des Augenblicks M., was wir als bezeichnen M. (nicht fett gedruckt) bezieht sich auf den Drehwinkel θ um den Schermodul G gemäß der folgenden Gleichung (abgeleitet durch ein einfaches Integral):
Da die Größe des Moments gleich dem Produkt des Moduls aus der Kraft F und dem Radius der Riemenscheibe R istp::
M = F.R.p
Und Stärke ist das Gewicht, das hängt W., dann:
M = W.R.p
Ersetzen der Größe des Augenblicks durch die Gleichung:
Es gibt die Beziehung zwischen Gewicht und Winkel:
Diese Beziehung zwischen den Variablen W. Y. θ ist linear, so dass die verschiedenen Winkel gemessen werden, die durch Aufhängen verschiedener Gewichte erzeugt werden.
Die Gewichts- und Winkelpaare werden auf Millimeterpapier aufgetragen, die beste Linie, die durch die Versuchspunkte verläuft, wird angepasst und die Steigung berechnet. m dieser Linie.
Eine Stange mit einer Länge von 2,5 Metern und einem Radius von 4,5 mm ist an einem Ende befestigt. Die andere ist mit einer Riemenscheibe mit einem Radius von 75 cm verbunden, die ein hängendes Gewicht W von 1,3 kg hat. Der Drehwinkel beträgt 9,5º.
Mit diesen Daten wird aufgefordert, den Schubmodul G des Stabes zu berechnen.
Aus der Gleichung:
G wird gelöscht:
Die in der Erklärung angegebenen Werte werden ersetzt, wobei darauf geachtet wird, dass alle Daten im Internationalen Einheitensystem SI ausgedrückt werden:
R = 4,5 mm = 4,5 × 10 -3 m
R.p = 75 cm = 0,075
Um von Kilogramm (die eigentlich Kilogramm sind - Kraft) zu Newton zu wechseln, multiplizieren Sie mit 9,8:
W = 1,3 kg Kraft = 1,3 · 9,8 N = 12,74 N.
Und schließlich müssen die Grade im Bogenmaß angegeben werden:
9,5 º = 9,5 x2π / 360 Radian = 0,1658 Radian.
Mit all dem haben Sie:
= 2,237 x 1010 Pa
Ein Würfel aus Gel hat eine Seite von 30 cm. Eine seiner Flächen ist fest, aber gleichzeitig wird eine parallele Kraft von 1 N auf die gegenüberliegende Fläche ausgeübt, die sich dank dieser 1 cm bewegt (siehe das Beispiel des Buches in Abbildung 1)..
Es wird gebeten, mit diesen Daten zu rechnen:
a) Die Größe der Scherspannung
b) Stamm δ
c) Der Wert des Schubmoduls
Die Größe der Scherspannung ist:
τ = F / A.
Mit:
A = Seitezwei = (30 x 10-zwei cm)zwei = 0,09 mzwei
Deshalb:
τ = 1 N / 0,09 mzwei = 11,1 Pa
Die Dehnung ist nichts anderes als der Wert von δ, gegeben durch:
δ = Δx / L.
Die Verschiebung des der Kraft unterworfenen Gesichts beträgt 1 cm, dann:
δ = 1/30 = 0,0333
Der Schubmodul ist der Quotient zwischen der Schubspannung und der Dehnung:
G = Scherspannung / Dehnung
Deshalb:
G = 11,1 Pa / 0,033 = 336,4 Pa
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.