Das assoziatives Eigentum der Summe repräsentiert den assoziativen Charakter der Summenoperation in verschiedenen mathematischen Mengen. Darin sind drei (oder mehr) Elemente dieser Mengen miteinander verbunden, die als a, b und c bezeichnet werden, so dass es immer wahr ist:
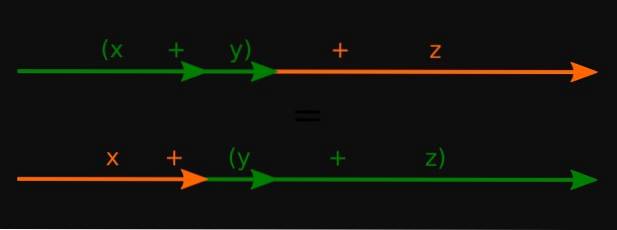
a + (b + c) = (a + b) + c
Auf diese Weise wird garantiert, dass unabhängig von der Art der Gruppierung zur Ausführung der Operation das gleiche Ergebnis erzielt wird.
Es ist jedoch zu beachten, dass die assoziative Eigenschaft nicht gleichbedeutend mit der kommutativen Eigenschaft ist. Das heißt, wir wissen, dass die Reihenfolge der Addenden die Summe nicht ändert oder dass die Reihenfolge der Faktoren das Produkt nicht verändert. Für die Summe kann es also so geschrieben werden: a + b = b + a.
In der assoziativen Eigenschaft ist dies jedoch anders, da die Reihenfolge der hinzuzufügenden Elemente beibehalten wird und sich die Operation ändert, die zuerst ausgeführt wird. Dies bedeutet, dass es nicht wichtig ist, zuerst (b + c) und zu diesem Ergebnis a hinzuzufügen, als a mit b hinzuzufügen und zum Ergebnis c hinzuzufügen.
Viele wichtige Operationen wie das Hinzufügen sind assoziativ, aber nicht alle. Zum Beispiel passiert bei der Subtraktion von reellen Zahlen Folgendes:
a - (b - c) ≠ (a - b) - c
Wenn a = 2, b = 3, c = 1, dann:
2- (3 - 1) ≠ (2 - 3) - 1
0 ≠ -2
Artikelverzeichnis
Wie für die Addition getan, besagt die assoziative Eigenschaft der Multiplikation, dass:
a ˟ (b ˟ c) = (a ˟ b) ˟ c
Bei reellen Zahlen kann leicht überprüft werden, ob dies immer der Fall ist. Zum Beispiel haben wir unter Verwendung der Werte a = 2, b = 3, c = 1:
zwei ˟ (3 ˟ 1) = (2 ˟ 3) ˟ 1 → 2 ˟ 3 = 6 ˟ 1
6 = 6
Reelle Zahlen erfüllen die assoziative Eigenschaft sowohl der Addition als auch der Multiplikation. Andererseits ist in einer anderen Menge, wie der von Vektoren, die Summe assoziativ, das Kreuzprodukt oder Vektorprodukt jedoch nicht..
Ein Vorteil von Operationen, bei denen die assoziative Eigenschaft erfüllt ist, besteht darin, dass sie auf die bequemste Weise gruppiert werden können. Dies erleichtert die Auflösung erheblich..
Angenommen, in einer kleinen Bibliothek gibt es 3 Regale mit jeweils 5 Regalen. In jedem Regal befinden sich 8 Bücher. Wie viele Bücher gibt es insgesamt??
Wir können den Vorgang folgendermaßen ausführen: Gesamtzahl der Bücher = (3 x 5) x 8 = 15 x 8 = 120 Bücher.
Oder so: 3 x (5 x 8) = 3 x 40 = 120 Bücher.
-In den Mengen natürlicher, ganzzahliger, rationaler, reeller und komplexer Zahlen ist die assoziative Eigenschaft der Addition und Multiplikation erfüllt.
-Für Polynome gilt auch bei diesen Operationen.
-Bei Operationen der Subtraktion, Division und Exponentiation ist die assoziative Eigenschaft weder in reellen Zahlen noch in Polynomen erfüllt.
-Im Fall von Matrizen gilt die assoziative Eigenschaft für Addition und Multiplikation, obwohl im letzteren Fall die Kommutativität nicht erfüllt ist. Dies bedeutet, dass angesichts der Matrizen A, B und C Folgendes zutrifft:
(A x B) x C = A x (B x C)
Aber ... A x B ≠ B x A.
Vektoren bilden eine andere Menge als reelle Zahlen oder komplexe Zahlen. Die für den Satz von Vektoren definierten Operationen sind etwas unterschiedlich: Es gibt Addition, Subtraktion und drei Arten von Produkten.
Die Summe der Vektoren erfüllt die assoziative Eigenschaft ebenso wie Zahlen, Polynome und Matrizen. Die Skalarprodukte, skalar nach Vektor und Kreuz, die zwischen Vektoren hergestellt werden, erfüllen diese nicht, aber das Skalarprodukt, bei dem es sich um eine andere Art von Operation zwischen Vektoren handelt, erfüllt sie unter Berücksichtigung der folgenden Punkte:
-Das Produkt aus einem Skalar und einem Vektor ergibt einen Vektor.
-Und wenn zwei Vektoren skalar multipliziert werden, ergibt sich ein Skalar.
Daher gegeben die Vektoren v, oder Y. w, und zusätzlich ein Skalar λ kann geschrieben werden:
-Summe der Vektoren: v +((oder + w ) = (v + oder) + w
-Skalarprodukt: λ (v • • oder ) = (λv) • oder
Letzteres ist dank möglich v • • oder ergibt einen Skalar und λv Es ist ein Vektor.
Jedoch:
v × ((oder × w ) ≠ (v × oder)×w
Diese Anwendung ist sehr interessant, da die assoziative Eigenschaft, wie bereits erwähnt, zur Lösung bestimmter Probleme beiträgt. Die Summe der Monome ist assoziativ und kann verwendet werden, um zu faktorisieren, wenn ein offensichtlicher gemeinsamer Faktor auf den ersten Blick nicht auftritt.
Angenommen, Sie fragen nach dem Faktor: x3 + zweixzwei + 3x +6. Dieses Polynom hat keinen gemeinsamen Faktor, aber lassen Sie uns sehen, was passiert, wenn es wie folgt gruppiert wird:
x3 + 2xzwei + 3x +6 = (x3 + 2xzwei) + (3x +6)
Die erste Klammer hat einen gemeinsamen Faktor xzwei::
x3 + zweixzwei = xzwei (x + 2)
Im zweiten ist der gemeinsame Faktor 3:
3x +6 = 3 (x + 2)
Dann:
x3 + zweixzwei + 3x +6 = xzwei(x + 2) + 3 (x + 2)
Jetzt gibt es einen offensichtlichen gemeinsamen Faktor: x + 2::
xzwei(x + 2) + 3 (x + 2) = (x + 2) (xzwei+3)
Ein Schulgebäude hat 4 Etagen und jeweils 12 Klassenzimmer mit 30 Schreibtischen. Wie viele Schreibtische hat die Schule insgesamt??
Dieses Problem wird gelöst, indem die assoziative Eigenschaft der Multiplikation angewendet wird.
Gesamtzahl der Schreibtische = 4 Stockwerke x 12 Klassenzimmer / Stockwerk x 30 Schreibtische / Klassenzimmer = (4 x 12) x 30 Schreibtische = 48 x 30 = 1440 Schreibtische.
Oder wenn Sie es vorziehen: 4 x (12 x 30) = 4 x 360 = 1440 Schreibtische
Angesichts der Polynome:
A (x) = 5x3 + 2xzwei -7x + 1
B (x) = x4 +6x3 -5x
C (x) = -8xzwei +3x -7
Wenden Sie die assoziative Eigenschaft der Addition an, um A (x) + B (x) + C (x) zu finden..
Sie können die ersten beiden gruppieren und die dritte zum Ergebnis hinzufügen:
A (x) + B (x) = [5x3 + 2xzwei -7x + 1] + [x4 +6x3 -5x] = x4 + 11x3+ 2xzwei -12x +1
Sofort wird das Polynom C (x) hinzugefügt:
[x4 + 11x3+ 2xzwei -12x +1] + [-8xzwei +3x -7] = x4 + 11x3 - 6xzwei -9x -6
Der Leser kann überprüfen, ob das Ergebnis identisch ist, wenn es mit der Option A (x) + [B (x) + C (x)] gelöst wird..
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.