
Nichtlineare Programmiermethoden und Übungen
Das nichtlineare Programmierung ist der Prozess der Optimierung einer Funktion, der von mehreren unabhängigen Variablen abhängt, die wiederum Einschränkungen unterliegen.
Wenn eine oder mehrere der Einschränkungen oder die Funktion zum Maximieren oder Minimieren (aufgerufen) Zielfunktion) wird es nicht als lineare Kombination der Variablen ausgedrückt, daher haben wir ein nichtlineares Programmierproblem.
Daher können die Verfahren und Methoden der linearen Programmierung nicht verwendet werden.
Beispielsweise kann die bekannte Methode nicht verwendet werden Simplex, Dies gilt nur, wenn die Zielfunktion und die Einschränkungen alle eine lineare Kombination der Problemvariablen sind.
Artikelverzeichnis
- 1 Methoden der linearen Programmierung
- 1.1 Lösungsbeispiel mit grafischer Methode
- 2 Übungen
- 2.1 - Übung 1 (grafische Methode)
- 2.2 - Übung 2 (Analysemethode: Lagrange-Multiplikatoren)
- 2.3 - Übung 3 (Nullgradient)
- 3 Referenzen
Lineare Programmiermethoden
Bei nichtlinearen Programmierproblemen sind folgende Hauptmethoden zu verwenden:
1.- Grafische Methoden.
2. Lagrange-Multiplikatoren, um die Grenze des Lösungsbereichs zu erkunden.
3.- Berechnung des Gradienten zur Untersuchung von Extremen der Zielfunktion.
4.- Die Methode zum Absteigen von Schritten, um die Nullgradientenpunkte zu finden.
5.- Modifizierte Methode der Lagrange-Multiplikatoren (mit der Karush-Kuhn-Tucker-Bedingung).
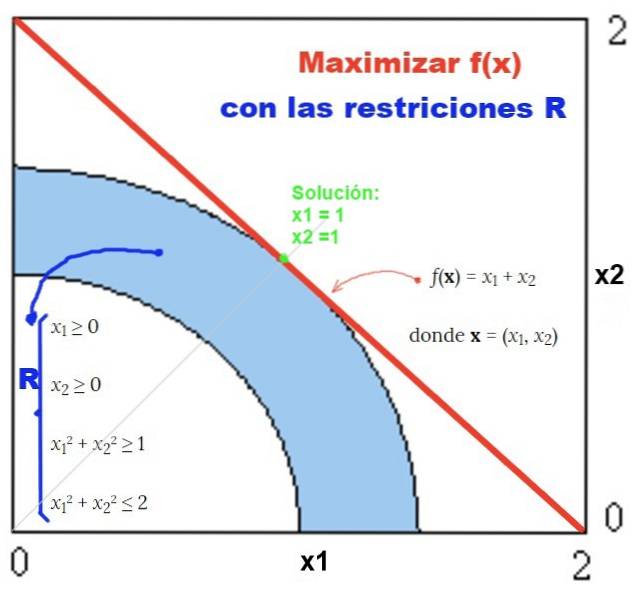
Lösungsbeispiel mit grafischer Methode
Ein Beispiel für eine Lösung mit der grafischen Methode ist die in Abbildung 2 gezeigte:
Ausbildung
- Übung 1 (Grafische Methode)
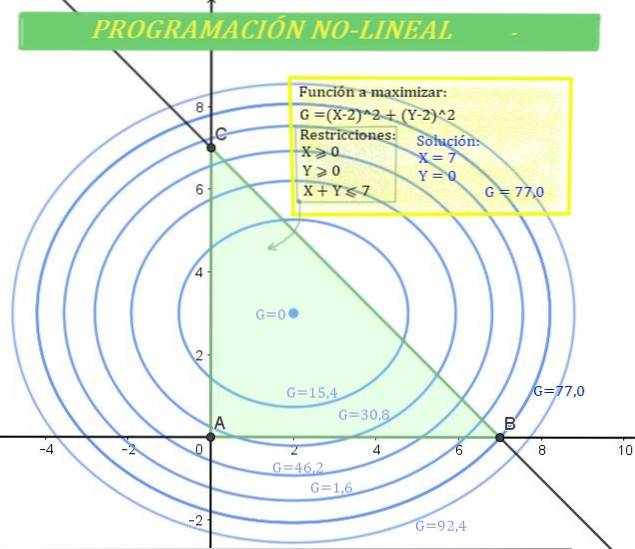
Der Gewinn G eines bestimmten Unternehmens hängt von der verkauften Menge des Produkts X und der verkauften Menge des Produkts Y ab. Außerdem wird der Gewinn durch die folgende Formel bestimmt:
G = 2 (X - 2)zwei + 3 (UND - 3)zwei
Es ist bekannt, dass die Beträge X und Y die folgenden Einschränkungen aufweisen:
X ≥ 0; Y ≥ 0 und X + Y ≤ 7
Bestimmen Sie die Werte von X und Y, die die maximale Verstärkung erzeugen.
Lösung
In diesem Problem ist die Zielfunktion nichtlinear, während die Ungleichungen, die die Einschränkungen definieren, sind. Es ist ein Problem von nichtlineare Programmierung.
Zur Lösung dieses Problems wird die grafische Methode gewählt.
Zunächst wird der Lösungsbereich bestimmt, der durch die Einschränkungen gegeben ist.
Als X ≥ 0; Y ≥ 0, die Lösung muss im ersten Quadranten der XY-Ebene gefunden werden, aber da es auch wahr sein muss, dass X + Y ≤ 7 ist, befindet sich die Lösung in der unteren Halbebene der Linie X + Y = 7.
Der Lösungsbereich ist der Schnittpunkt des ersten Quadranten mit der unteren Halbebene der Linie, wodurch ein dreieckiger Bereich entsteht, in dem sich die Lösung befindet. Es ist das gleiche wie in Abbildung 1 gezeigt.
Andererseits kann die Verstärkung G auch in der kartesischen Ebene dargestellt werden, da ihre Gleichung die einer Ellipse mit Zentrum (2,3) ist..
Die Ellipse ist in Abbildung 1 für verschiedene Werte von G dargestellt. Je höher der Wert von G ist, desto größer ist die Verstärkung..
Es gibt Lösungen, die zur Region gehören, aber nicht den maximalen G-Wert angeben, während andere, wie z. B. G = 92,4, außerhalb der grünen Zone, dh der Lösungszone, liegen.
Dann entspricht der Maximalwert von G, so dass X und Y zum Lösungsbereich gehören:
G = 77 (maximale Verstärkung), die für X = 7 und Y = 0 angegeben ist.
Interessanterweise tritt der maximale Gewinn auf, wenn die Verkaufsmenge von Produkt Y Null ist, während die Menge von Produkt X ihren höchstmöglichen Wert erreicht..
- Übung 2 (Analysemethode: Lagrange-Multiplikatoren)
Finden Sie die Lösung (x, y), die die Funktion f (x, y) = x machtzwei + 2 undzwei sei maximal im Bereich g (x, y) = xzwei + Y.zwei - 1 = 0.
Lösung
Es ist eindeutig ein nichtlineares Programmierproblem, da sowohl die Zielfunktion f (x, y) als auch die Beschränkung g (x, y) = 0 keine lineare Kombination der Variablen x und y sind.
Es wird die Lagrange-Multiplikatormethode verwendet, bei der zunächst die Lagrange-Funktion L (x, y, λ) definiert werden muss:
L (x, y, λ) = f (x, y) - λg (x, y) = xzwei + 2 undzwei - λ (xzwei + Y.zwei - 1)
Wobei λ ein Parameter mit dem Namen ist Lagrange-Multiplikator.
Um die Extremwerte der Zielfunktion f in dem durch die Restriktion g (x, y) = 0 gegebenen Lösungsbereich zu bestimmen, gehen Sie folgendermaßen vor:
-Finden Sie die partiellen Ableitungen der Lagrange-Funktion L in Bezug auf x, y, λ.
-Setzen Sie jede Ableitung auf Null.
Hier ist die Reihenfolge dieser Operationen:
- ∂L / ∂x = 2x - 2λx = 0
- ∂L / ∂y = 4y - 2λy = 0
- ∂L / ∂λ = - (xzwei + Y.zwei - 1) = 0
Mögliche Systemlösungen
Eine mögliche Lösung dieses Systems ist λ = 1, so dass die erste Gleichung erfüllt ist, in welchem Fall y = 0, so dass die zweite erfüllt ist.
Diese Lösung impliziert, dass x = 1 oder x = -1 ist, damit die dritte Gleichung erfüllt wird. Auf diese Weise wurden zwei Lösungen S1 und S2 erhalten:
S1: (x = 1, y = 0)
S2: (x = -1, y = 0).
Die andere Alternative ist, dass λ = 2 ist, so dass die zweite Gleichung unabhängig vom Wert y erfüllt ist.
In diesem Fall ist die einzige Möglichkeit, die erste Gleichung zu erfüllen, dass x = 0 ist. In Anbetracht der dritten Gleichung gibt es nur zwei mögliche Lösungen, die wir S3 und S4 nennen werden:
S3: (x = 0, y = 1)
S4: (x = 0, y = -1)
Um herauszufinden, welche oder welche dieser Lösungen die Zielfunktion maximieren, setzen wir f (x, y) ein:
S1: f (1, 0) = 1zwei + 2.0zwei = 1
S2: f (-1, 0) = (-1)zwei + 2.0zwei = 1
S3: f (0, 1) = 0zwei + 2.1zwei = 2
S4: f (0, -1) = 0zwei + einundzwanzig)zwei = 2
Wir schließen daraus, dass die Lösungen, die f maximieren, wenn x und y zum Umfang g (x, y) = 0 gehören, S3 und S4 sind.
Die Wertepaare (x = 0, y = 1) und (x = 0, y = -1) maximieren f (x, y) im Lösungsbereich g (x, y) = 0.
- Übung 3 (Nullgradient)
Finden Sie Lösungen (x, y) für die Zielfunktion:
f (x, y) = xzwei + 2 undzwei
Sei maximal im Bereich g (x, y) = xzwei + Y.zwei - 1 ≤ 0.
Lösung
Diese Übung ähnelt Übung 2, aber der Lösungs- (oder Restriktions-) Bereich erstreckt sich auf den inneren Bereich des Umfangs g (x, y) = 0, dh auf den Kreis g (x, y) ≤ 0. Dies schließt ein zum Umfang und seinem inneren Bereich.
Die Lösung an der Grenze wurde bereits in Übung 2 festgelegt, die innere Region muss jedoch noch untersucht werden.
Dazu muss der Gradient der Funktion f (x, y) berechnet und gleich Null gesetzt werden, um Extremwerte im Lösungsbereich zu finden. Dies entspricht der Berechnung der partiellen Ableitungen von f in Bezug auf x bzw. y und der Einstellung gleich Null:
∂f / ∂x = 2 x = 0
∂f / ∂y = 4 y = 0
Dieses Gleichungssystem hat als einzige Lösung (x = 0, y = 0), die zum Kreis g (x, y) ≤ 0 gehört.
Das Einsetzen dieses Wertes in die Funktion f führt zu:
f (0, 0) = 0
Zusammenfassend ist der Maximalwert, den die Funktion im Lösungsbereich annimmt, 2 und tritt an der Grenze des Lösungsbereichs für die Werte (x = 0, y = 1) und (x = 0, y = -1) auf ).
Verweise
- Avriel, M. 2003. Nichtlineare Programmierung. Dover Publishing.
- Bazaraa. 1979. Nichtlineare Programmierung. John Wiley & Sons.
- Bertsekas, D. 1999. Nichtlineare Programmierung: 2. Auflage. Athena Scientific.
- Nocedal, J. 1999. Numerical Optimization. Springer-Verlag.
- Wikipedia. Nichtlineare Programmierung. Wiederhergestellt von: es.wikipedia.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.