
Frequenzwahrscheinlichkeitskonzept, wie es berechnet wird und Beispiele
Das Frequenzwahrscheinlichkeit ist eine Unterdefinition innerhalb der Untersuchung der Wahrscheinlichkeit und ihrer Phänomene. Seine Untersuchungsmethode in Bezug auf Ereignisse und Attribute basiert auf einer großen Anzahl von Iterationen, wodurch der Trend jedes einzelnen langfristig oder sogar bei unendlichen Wiederholungen beobachtet wird..
Zum Beispiel enthält ein Umschlag mit Gummis 5 Radiergummis jeder Farbe: blau, rot, grün und gelb. Wir wollen die Wahrscheinlichkeit bestimmen, dass jede Farbe nach einer zufälligen Auswahl herauskommen muss.

Es ist mühsam, sich vorzustellen, wie man einen Gummi herausnimmt, registriert, zurückgibt, einen Gummi herausnimmt und dasselbe mehrere hundert oder mehrere tausend Mal wiederholt. Möglicherweise möchten Sie das Verhalten sogar nach mehreren Millionen Iterationen beobachten.
Im Gegenteil, es ist interessant festzustellen, dass nach einigen Wiederholungen die erwartete Wahrscheinlichkeit von 25% nicht vollständig erfüllt ist, zumindest nicht für alle Farben nach 100 Iterationen..
Unter dem Ansatz der Frequenzwahrscheinlichkeit erfolgt die Zuweisung der Werte nur durch das Studium vieler Iterationen. Auf diese Weise muss der Prozess vorzugsweise computergestützt oder emuliert ausgeführt und registriert werden.
Mehrere Ströme lehnen die Frequenzwahrscheinlichkeit ab, was auf einen Mangel an Empirismus und Zuverlässigkeit bei den Zufälligkeitskriterien hinweist.
Artikelverzeichnis
- 1 Wie berechnet sich die Frequenzwahrscheinlichkeit??
- 1.1 Gesetz der großen Zahlen
- 2 Andere Ansätze zur Wahrscheinlichkeit
- 2.1 Logische Theorie
- 2.2 Subjektive Theorie
- 3 Geschichte
- 3.1 Massenphänomene und sich wiederholende Ereignisse
- 3.2 Attribute
- 4 Beispiel
- 4.1 Referenzen
Wie berechnet sich die Frequenzwahrscheinlichkeit??
Durch Programmieren des Experiments in einer beliebigen Schnittstelle, die eine rein zufällige Iteration bieten kann, kann begonnen werden, die Frequenzwahrscheinlichkeit des Phänomens anhand einer Wertetabelle zu untersuchen.
Das vorige Beispiel ist aus dem Frequenzansatz ersichtlich:
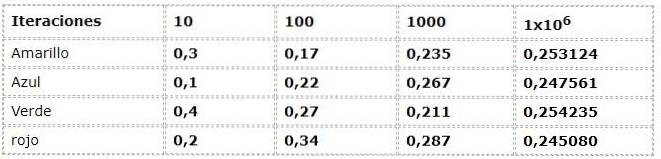
Die numerischen Daten entsprechen dem Ausdruck:
N (a) = Anzahl der Vorkommen / Anzahl der Iterationen
Wobei N (a) die relative Häufigkeit des Ereignisses "a" darstellt.
"A" gehört zu der Menge möglicher Ergebnisse oder des Probenraums Ω
Ω: rot, grün, blau, gelb
Eine beträchtliche Streuung wird in den ersten Iterationen geschätzt, wenn Frequenzen mit bis zu 30% Unterschieden zwischen ihnen beobachtet werden. Dies sind sehr hohe Daten für ein Experiment, das theoretisch Ereignisse mit der gleichen Möglichkeit aufweist (gleich wahrscheinlich)..
Mit zunehmenden Iterationen scheinen sich die Werte jedoch immer mehr an die Werte anzupassen, die durch den theoretischen und logischen Strom dargestellt werden.
Gesetz der großen Zahlen
Als unerwartete Übereinstimmung zwischen dem theoretischen und dem Frequenzansatz entsteht das Gesetz der großen Zahlen. Wo festgestellt wird, dass sich die Werte des Frequenzexperiments nach einer beträchtlichen Anzahl von Iterationen den theoretischen Werten nähern.
Im Beispiel können Sie sehen, wie sich die Werte 0,250 nähern, wenn die Iterationen zunehmen. Dieses Phänomen ist elementar in den Schlussfolgerungen vieler probabilistischer Arbeiten.

Andere Ansätze zur Wahrscheinlichkeit
Es gibt zwei weitere Theorien oder Ansätze zum Begriff der Wahrscheinlichkeit zusätzlich zu den Frequenzwahrscheinlichkeit.
Logische Theorie
Sein Ansatz orientiert sich an der deduktiven Logik von Phänomenen. Im vorherigen Beispiel beträgt die Wahrscheinlichkeit, jede Farbe auf geschlossene Weise zu erhalten, 25%. Das heißt, ihre Definitionen und Axiome berücksichtigen keine Verzögerungen außerhalb ihres Bereichs probabilistischer Daten..
Subjektive Theorie
Es basiert auf dem Wissen und den früheren Überzeugungen, die jeder Einzelne über die Phänomene und Eigenschaften hat. Aussagen wie „Es regnet immer zu Ostern " Sie sind auf ein Muster ähnlicher Ereignisse zurückzuführen, die zuvor aufgetreten sind.
Geschichte
Die Anfänge seiner Umsetzung reichen bis ins 19. Jahrhundert zurück, als Venn sie in mehreren seiner Werke in Cambridge, England, zitierte. Aber erst im 20. Jahrhundert entwickelten und formten zwei statistische Mathematiker die Frequenzwahrscheinlichkeit.
Einer von ihnen war Hans Reichenbach, der seine Arbeiten in Publikationen wie "The Theory of Probability" aus dem Jahr 1949 entwickelt.
Der andere war Richard Von Mises, der seine Arbeit durch mehrere Veröffentlichungen weiterentwickelte und vorschlug, die Wahrscheinlichkeit als mathematische Wissenschaft zu betrachten. Dieses Konzept war neu in der Mathematik und würde eine Ära des Wachstums im Studium der Mathematik einleiten. Frequenzwahrscheinlichkeit.
Tatsächlich ist diese Veranstaltung der einzige Unterschied zu den Beiträgen der Generation Venn, Cournot und Helm. Wo die Wahrscheinlichkeit zu Wissenschaften wie Geometrie und Mechanik homolog wird.
< La teoría de las probabilidades trata con massive Phänomene und sich wiederholende Ereignisse. Probleme, bei denen entweder dasselbe Ereignis immer wieder wiederholt wird oder eine große Anzahl einheitlicher Elemente gleichzeitig beteiligt sind> Richard Von Mises
Massive Phänomene und sich wiederholende Ereignisse
Drei Typen können klassifiziert werden:
- Physisch: Sie gehorchen Naturmustern jenseits eines Zufallszustands. Zum Beispiel das Verhalten der Moleküle eines Elements in einer Probe.
- Zufall - Ihre Hauptüberlegung ist die Zufälligkeit, z. B. das wiederholte Würfeln.
- Biologische Statistik: Auswahl der Testpersonen nach ihren Merkmalen und Eigenschaften.
Theoretisch spielt das Individuum, das misst, eine Rolle in den Wahrscheinlichkeitsdaten, weil es sein Wissen und seine Erfahrungen sind, die diesen Wert oder diese Vorhersage artikulieren..
In dem Frequenzwahrscheinlichkeit Die Ereignisse werden als zu behandelnde Sammlungen betrachtet, bei denen die Person bei der Schätzung keine Rolle spielt.
Attribute
In jedem Element tritt ein Attribut auf, das je nach Art variabel ist. Beispielsweise haben die Wassermoleküle bei der Art des physikalischen Phänomens unterschiedliche Geschwindigkeiten..
Im Würfelwurf kennen wir den Probenraum Ω, der die Attribute des Experiments darstellt.
Ω: 1, 2, 3, 4, 5, 6
Es gibt andere Attribute, wie z. B. gerade ΩP. oder ungerade Ω seinich
Ωp : 2, 4, 6
Ωich : 1, 3, 5
Welches kann als nicht-elementare Attribute definiert werden.
Beispiel
- Wir wollen die Häufigkeit jeder möglichen Summe beim Werfen von zwei Würfeln berechnen.
Zu diesem Zweck wird ein Experiment programmiert, bei dem in jeder Iteration zwei Quellen für Zufallswerte zwischen [1, 6] hinzugefügt werden.
Die Daten werden in einer Tabelle aufgezeichnet und Trends in großer Anzahl untersucht.
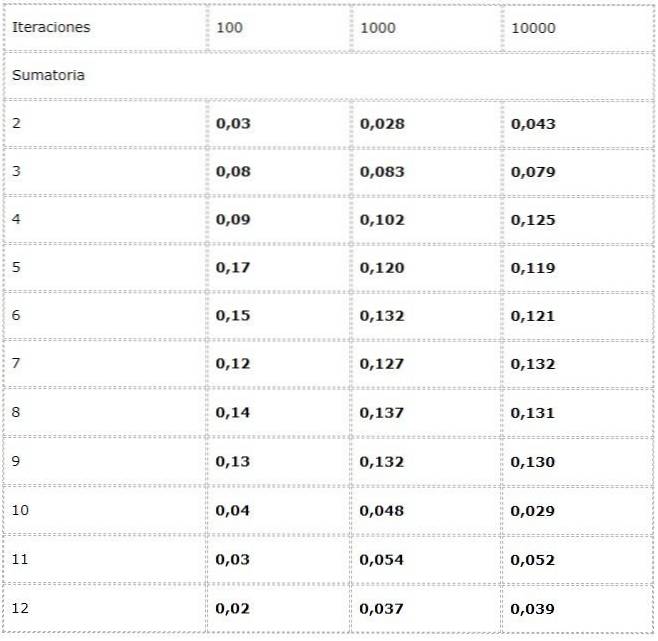
Es wird beobachtet, dass die Ergebnisse zwischen den Iterationen erheblich variieren können. Das Gesetz der großen Zahlen zeigt sich jedoch in der offensichtlichen Konvergenz, die in den letzten beiden Spalten dargestellt ist.
Verweise
- Statistik und Evidenzbewertung für Forensiker. Zweite Ausgabe. Colin G.G. Aitken. Schule der Mathematik. Die Universität von Edinburgh, UK
- Mathematik für die Informatik. Eric Lehman. Google Inc.
F Thomson Leighton Department für Mathematik und das Labor für Informatik und KI, Massachusetts Institute of Technology; Akamai Technologies - The Arithmetic Teacher, Band 29. Nationaler Rat der Lehrer für Mathematik, 1981. University of Michigan.
- Zahlentheorie lernen und lehren: Kognitions- und Unterrichtsforschung / herausgegeben von Stephen R. Campbell und Rina Zazkis. Ablex Publishing 88 Post Road West, Westport CT 06881
- Bernoulli, J. (1987). Ars Conjectandi- 4ème partie. Rouen: IREM.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.