
Regelmäßige Polygoneigenschaften, Elemente, Winkel, Beispiele
Das regelmäßige Polygone sind diejenigen, bei denen alle Seiten und Innenwinkel gleich sind. In der folgenden Abbildung gibt es eine Reihe verschiedener Polygone, bei denen es sich um ebene Figuren handelt, die durch eine geschlossene Kurve begrenzt sind, und nur diejenigen, die hervorgehoben sind, erfüllen die Bedingungen, um regelmäßig zu sein.
Zum Beispiel ist das gleichseitige Dreieck ein regelmäßiges Polygon, da seine drei Seiten das gleiche Maß haben sowie seine Innenwinkel, die jeweils 60 ° wert sind..
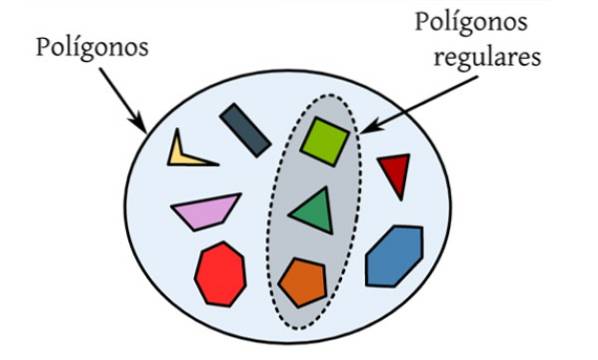
Das Quadrat ist ein Viereck mit vier gleich großen Seiten und einem Innenwinkel von 90 °. Es folgt das reguläre Fünfeck mit fünf gleich großen Seiten und fünf Innenwinkeln von jeweils 108 °..
Wenn ein Polygon regulär ist, wird dieses Wort zu seinem speziellen Namen hinzugefügt, sodass wir das reguläre Sechseck, das reguläre Siebeneck usw. haben.
Artikelverzeichnis
- 1 Eigenschaften regulärer Polygone
- 2 Elemente eines regulären Polygons
- 2.1 Scheitelpunkt
- 2.2 Seite
- 2.3 Diagonale
- 2.4 Zentrum
- 2.5 Radio
- 2.6 Apothem
- 2.7 Zentralwinkel
- 2,8 Sagita
- 3 Umfang und Fläche
- 3.1 Umfang
- 3.2 Fläche
- 4 Winkel
- 4.1 Zentralwinkel
- 4.2 Innenwinkel oder Innenwinkel
- 4.3 Außenwinkel
- 5 Beispiele für reguläre Polygone
- 5.1 - Regelmäßige Polygone im täglichen Leben und in der Natur
- 5.2 - Regelmäßige Sechsecke in der Natur
- 6 Übung gelöst
- 6.1 Lösung
- 7 Referenzen
Eigenschaften regulärer Polygone
Die wichtigsten Eigenschaften regulärer Polygone lassen sich wie folgt zusammenfassen:
-Die Seiten messen das gleiche, deshalb sind sie gleichseitig.
-Sie sind gleichwinklig, da alle seine Innenwinkel das gleiche Maß haben.
-Sie können immer in einem Umfang eingeschrieben werden, was bedeutet, dass sie perfekt in einen passen, der genannt wird umschriebener Umfang.
-Für ein reguläres Polygon mit n Seiten ist das Maß eines Innenwinkels α:
α = [180 (n-2)] / n
-Sie können n (n-3) / 2 Diagonalen aus den Eckpunkten eines Polygons zeichnen, unabhängig davon, ob es regulär ist oder nicht.
-Die Summe der Außenwinkel ist gleich 360º.

Elemente eines regulären Polygons
Als nächstes präsentieren wir die Hauptelemente eines regulären Polygons, die in der folgenden Abbildung dargestellt sind.

Scheitel
Gemeinsamer Punkt, den zwei aufeinanderfolgende Seiten haben, in der Figur als V bezeichnet.
Seite
Es ist das Segment, das zwei aufeinanderfolgende Eckpunkte des Polygons verbindet und als ℓ oder L bezeichnet wird.
Diagonale
Segment, das zwei nicht aufeinanderfolgende Eckpunkte des Polygons verbindet, wird in der Abbildung als bezeichnet d.
Center
Es ist das gemeinsame Zentrum des eingeschriebenen Kreises und des umschriebenen Kreises, bezeichnet mit dem Buchstaben O. Es kann auch als der einzige Punkt angesehen werden, der sowohl von den Eckpunkten als auch von den Mittelpunkten jeder Seite gleich weit entfernt ist..
Radio
Es ist das Radio r des umschriebenen Kreises und fällt mit dem Abstand zwischen O und einem Scheitelpunkt zusammen.
Apothema
Es wird genannt Apothema auf den Radius des im Polygon eingeschriebenen Umfangs, der in der Figur mit einem Buchstaben dargestellt ist zu. Das Apothem steht senkrecht zu einer Seite und verbindet es mit dem Zentrum O (rotes Segment in Abbildung 3)..
Bei Kenntnis des Radius r und der Länge der Seite wird das Apothem berechnet durch:
Da das Apothem tatsächlich eines der Beine eines rechtwinkligen Dreiecks ist (siehe Abbildung 3), ist das andere Bein der Wert von ℓ / 2 (halbe Seite) und die Hypotenuse der Radius r des Polygons.
Wenn der Satz von Pythagoras auf das Dreieck angewendet wird, erhält man diese Gleichung, die nicht nur für das Sechseck, sondern für jedes reguläre Polygon gilt.
Zentralwinkel
Es ist der Winkel, dessen Scheitelpunkt mit dem Zentrum O zusammenfällt und dessen Seiten die Segmente sind, die das Zentrum mit zwei aufeinanderfolgenden Scheitelpunkten verbinden. Sein Maß in sexagesimalen Graden beträgt 360º / n, wobei n ist die Anzahl der Seiten des Polygons.
Sagita
Dies ist der Unterschied zwischen dem Radius des Polygons und dem Apothem (siehe Abbildung 3). Bezeichnet die Sagitta als S:
S = r - a
Umfang und Fläche
Umfang
Es kann leicht berechnet werden, indem die Längen der Seiten addiert werden. Da jede Seite die gleiche Länge L hat und es n Seiten gibt, wird der Umfang P ausgedrückt als:
P = n.L.
Bereich
In einem regulären Polygon ist die Fläche A durch das Produkt zwischen dem Halbumfang (der Hälfte des Umfangs) und der Länge des Apothems gegeben zu.
A = P.a / 2
Da der Umfang von der Anzahl der Seiten n abhängt, stellt sich heraus, dass:
A = (nL) .a / 2
Zwei reguläre Polygone können den gleichen Umfang haben, auch wenn sie nicht die gleiche Anzahl von Seiten haben, da dies dann von der Länge der Seiten abhängen würde.
In Buch V von ihm Sammlung, Der Mathematiker Pappus von Alexandria (290-350), der letzte der großen antiken griechischen Mathematiker, zeigte, dass unter allen regulären Polygonen mit demselben Umfang dasjenige mit der größten Fläche das mit der größten Anzahl von Seiten ist.
Winkel
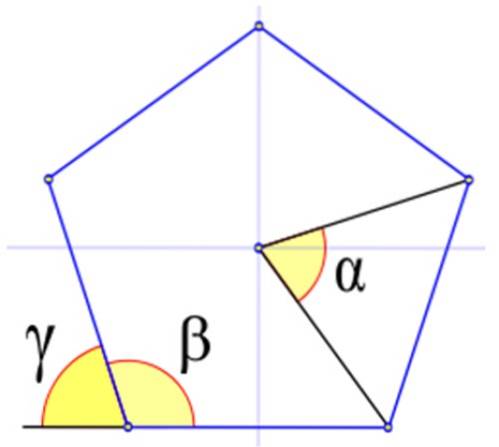
Abbildung 4 zeigt die relevanten Winkel in einem regulären Polygon, die mit den griechischen Buchstaben α, β und γ bezeichnet sind.
Zentralwinkel
Zuvor haben wir den zentralen Winkel zwischen den Elementen des regulären Polygons erwähnt. Dies ist der Winkel, dessen Scheitelpunkt in der Mitte des Polygons liegt, und die Seiten sind die Segmente, die die Mitte mit zwei aufeinanderfolgenden Scheitelpunkten verbinden.
Um das Maß des Mittelwinkels α zu berechnen, teilen Sie 360º durch n, die Anzahl der Seiten. Oder 2π Radiant zwischen n:
α = 360º / n
Entspricht im Bogenmaß:
α = 2π / n
Innenwinkel oder Innenwinkel
In Fig. 4 ist der Innenwinkel β derjenige, dessen Scheitelpunkt mit einem der Figuren zusammenfällt und dessen Seiten ebenfalls Seiten der Figur sind. Es wird in sexagesimalen Graden berechnet durch:
β = [180 (n-2)] / n
Oder im Bogenmaß mit:
β = [π (n-2)] / n
Außenwinkel
Sie werden mit dem griechischen Buchstaben γ bezeichnet. Die Figur zeigt, dass γ + β = 180º ist. Deshalb:
γ = 180º - β
Die Summe aller Außenwinkel zu einem regulären Polygon beträgt 360º.

Beispiele für reguläre Polygone
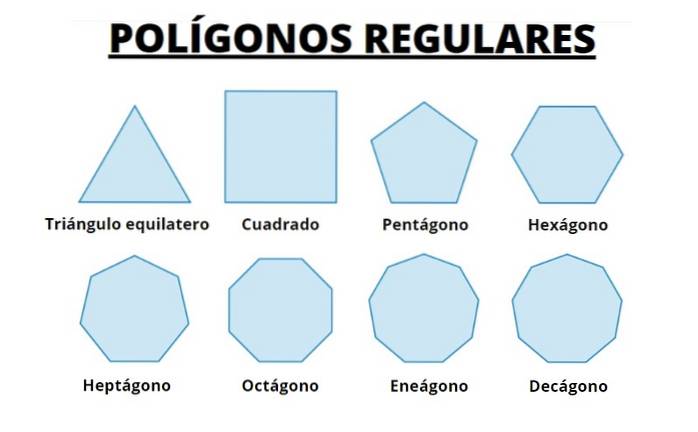
Als nächstes haben wir die ersten 8 regulären Polygone. Wir beobachten, dass das Polygon mit zunehmender Anzahl von Seiten zunehmend dem Umfang ähnelt, in den sie eingeschrieben sind.
Wir können uns vorstellen, dass wir den Umfang erhalten, indem wir die Länge der Seiten immer kleiner machen und deren Anzahl erhöhen.
- Regelmäßige Polygone im täglichen Leben und in der Natur
Regelmäßige Polygone finden sich überall im Alltag und sogar in der Natur. Schauen wir uns einige Beispiele an:
Ampeln
Regelmäßige Polygone wie gleichseitige Dreiecke, Quadrate und Rauten sind in der Beschilderung, die wir auf Autobahnen und Straßen sehen, reichlich vorhanden. In Abbildung 6 sehen wir ein Stoppschild mit einer achteckigen Form.

Möbel
Unzählige Möbelstücke haben zum Beispiel das Quadrat als charakteristische geometrische Figur, ebenso wie viele Tische, Stühle und Bänke quadratisch sind. Ein Parallelepiped ist im Allgemeinen eine Box mit Seiten in Form eines Rechtecks (das kein reguläres Polygon ist), aber sie können auch quadratisch gemacht werden..
Architektur und Bau
Die Fliesen an Böden und Wänden, sowohl in Häusern als auch auf der Straße, sind oft wie normale Polygone geformt..
Tessellationen sind Oberflächen, die vollständig mit Fliesen bedeckt sind, die unterschiedliche geometrische Formen haben. Mit dem Dreieck, dem Quadrat und dem Sechseck können Sie regelmäßige Tessellationen erstellen, die nur einen einzigen Figurentyp verwenden, um perfekt abzudecken, ohne Leerzeichen zu lassen (siehe Abbildung 6)..
Ebenso verwenden Gebäude regelmäßige Polygone in Elementen wie Fenstern und Dekoration..

- Regelmäßige Sechsecke in der Natur
Überraschenderweise ist das reguläre Sechseck ein Polygon, das in der Natur häufig vorkommt..
Die Kämme, die Bienen zur Speicherung von Honig herstellen, sind sehr nahe an einem regelmäßigen Sechseck geformt. Wie Pappus von Alexandria feststellte, optimieren die Bienen auf diese Weise den Raum, um so viel Honig wie möglich zu speichern..
Und es gibt auch regelmäßige Sechsecke in der Schale der Schildkröten und der Schneeflocken, die auch verschiedene sehr schöne geometrische Formen annehmen..
Übung gelöst
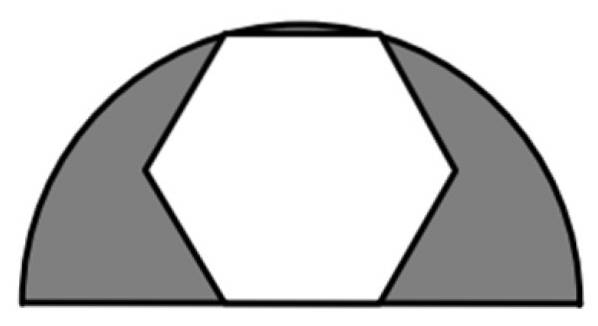
Ein regelmäßiges Sechseck ist in einem Halbkreis mit einem Radius von 6 cm eingeschrieben, wie in der Abbildung gezeigt. Was ist der Wert des schattierten Bereichs??
Lösung
Die schattierte Fläche ist die Differenz zwischen der Fläche des Halbkreises mit dem Radius R = 6 cm und der Fläche des gesamten Sechsecks, einem regelmäßigen 6-seitigen Polygon. Wir brauchen also Formeln für den Bereich jeder dieser Figuren.
Halbkreisbereich
ZU1 = π R.zwei / 2 = π (6 cm)zwei / 2 = 18 & pgr; cmzwei
Regelmäßiger Sechseckbereich
Die Formel zur Berechnung der Fläche eines regulären Polygons lautet:
A = P.a / 2
Wo P. ist der Umfang und zu ist das Apothem. Da der Umfang die Summe der Seiten ist, benötigen wir den Wert dieser. Für das reguläre Sechseck:
P = 6ℓ
Deshalb:
A = 6ℓa / 2
Um den Wert der Seite find zu ermitteln, müssen Hilfsfiguren konstruiert werden, die wir nachfolgend erläutern werden:
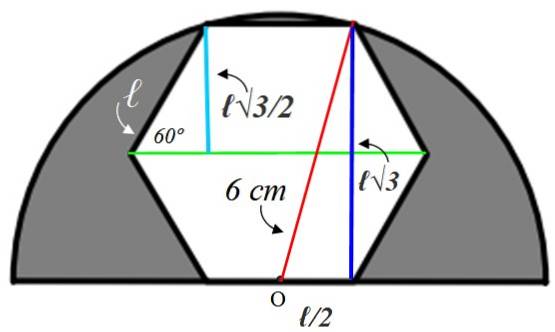
Beginnen wir mit dem kleinen rechten Dreieck links, dessen Hypotenuse ℓ ist. Ein Innenwinkel des Sechsecks ist gleich:
α = [180 (n-2)] / n = α = [180 (6-2)] / 6 = 120º
Der Radius, den wir grün gezeichnet haben, halbiert diesen Winkel, daher beträgt der spitze Winkel des kleinen Dreiecks 60º. Mit den bereitgestellten Informationen wird dieses Dreieck gelöst und die hellblaue Seite gefunden, die das gleiche wie das Apothem misst:
Gegenüberliegendes Bein = a = ℓ x sin 60º = ℓ√3 / 2 cm
Dieser Wert Es ist das Doppelte vom dunkelblauen Bein des großen Dreiecks rechts, aber aus diesem Dreieck wissen wir, dass die Hypotenuse 6 cm misst, weil es der Radius des Halbkreises ist. Das verbleibende Bein (unten) ist gleich ℓ / 2, da sich Punkt O in der Mitte der Seite befindet.
Da Innenwinkel dieses Dreiecks nicht bekannt sind, können wir den Satz von Pythagoras dafür angeben:
36 = 3 ℓzwei + ℓzwei / 4
(13/4) ℓzwei = 36 → ℓ = √ (4 x 36) / 13 cm = 12 / √ 13 cm
Mit diesem Wert wird das Apothem berechnet:
a = 3√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm
Lass uns anrufenzwei zum Bereich des regulären Sechsecks:

= 28,8 cmzwei
Schattierter Figurenbereich
ZU1 - ZUzwei = 18 & pgr; cmzwei - 28,8 cmzwei = 27,7 cmzwei
Verweise
- Baldor, A. 1973. Geometrie und Trigonometrie. Zentralamerikanischer Kulturverlag.
- Viel Spaß mit Mathe. Tessellationen. Wiederhergestellt von: gustolasmatematicas.com.
- E. A. 2003. Elemente der Geometrie: mit Übungen und Kompassgeometrie. Universität von Medellin.
- Sechsecke in der Natur. Wiederhergestellt von: malvargamath.wordpress.com.
- Jiménez, R. 2010. Mathematik II. Geometrie und Trigonometrie. Zweite Ausgabe. Prentice Halle.
- Regelmäßige Polygone. Wiederhergestellt von: mate.ingenieria.usac.edu.gt.
- Wikipedia. Apothema. Wiederhergestellt von: es.wikipedia.org.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.