Transzendente Zahlen, was sind sie, Formeln, Beispiele, Übungen

Das transzendente Zahlen sind solche, die aufgrund einer Polynomgleichung nicht erhalten werden können. Das Gegenteil einer transzendenten Zahl ist a algebraische Zahl, Welches sind Lösungen einer Polynomgleichung vom Typ:

zu_n xⁿ + zu_n-1 x^n-1 +… + A._zwei x^zwei + zu₁ x + a₀ = 0

Wo die Koeffizienten a_n, zu_n-1,… Zu_zwei, zu₁, zu₀ sind rationale Zahlen, die als Koeffizienten des Polynoms. Wenn eine Zahl x eine Lösung für die vorherige Gleichung ist, ist diese Zahl nicht transzendent.

Wir werden einige Zahlen analysieren und sehen, ob sie transzendent sind oder nicht:

a) 3 ist nicht transzendent, weil es eine Lösung von x - 3 = 0 ist.

b) -2 kann nicht transzendent sein, da es sich um eine Lösung von x + 2 = 0 handelt.

c) ⅓ ist eine Lösung von 3x - 1 = 0

d) Eine Lösung der Gleichung x^zwei - 2x + 1 = 0 ist √2 -1, so dass die Zahl per Definition nicht transzendent ist.

e) Weder ist √2, weil es das Ergebnis der Gleichung x ist^zwei - 2 = 0. Quadrieren √2 ergibt das Ergebnis 2, das von 2 subtrahiert wird, ist gleich Null. √2 ist also eine irrationale Zahl, aber sie ist nicht transzendent.

Artikelverzeichnis

• 1 Was sind transzendente Zahlen??
  • 1.1 Die Zahl π
  • 1.2 Die Nummer e
• 2 Formeln, in denen die transzendente Zahl π erscheint
  • 2.1 Der Umfang des Umfangs
  • 2.2 Fläche eines Kreises
  • 2.3 Oberfläche einer Kugel
  • 2.4 Volumen der Kugel
• 3 Übungen
  • 3.1 - Übung 1
  • 3.2 - Übung 2
• 4 Referenzen

Was sind transzendente Zahlen??

Das Problem ist, dass es keine allgemeine Regel gibt, um sie zu erhalten (später werden wir einen Weg sagen), aber einige der bekanntesten sind die Zahlen Pi und der Neper Nummer, bezeichnet jeweils mit: π Y. und.

Die Zahl π

Die Nummer π Es erscheint natürlich, wenn man beobachtet, dass der mathematische Quotient zwischen dem Umfang P eines Kreises und seinem Durchmesser D, unabhängig davon, ob es sich um einen kleinen oder einen großen Kreis handelt, immer die gleiche Zahl ergibt, die genannt wird Pi::

π = P / D ≈ 3,14159…

Dies bedeutet, dass, wenn der Durchmesser des Umfangs als Maßeinheit genommen wird, für alle, ob groß oder klein, der Umfang immer P = 3,14… = ist π, wie in der Animation von Abbildung 2 zu sehen ist.

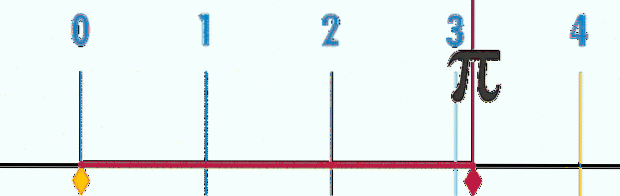
Um mehr Dezimalstellen zu bestimmen, ist es notwendig, P und D genauer zu messen und dann den Quotienten zu berechnen, was mathematisch durchgeführt wurde. Die Quintessenz ist, dass die Dezimalstellen des Quotienten kein Ende haben und sich nie wiederholen, also die Zahl π es ist nicht nur transzendent, sondern auch transzendent irrational.

Eine irrationale Zahl ist eine Zahl, die nicht als Division zweier ganzer Zahlen ausgedrückt werden kann. 

Es ist bekannt, dass jede transzendente Zahl irrational ist, aber es ist nicht wahr, dass alle irrationalen Zahlen transzendent sind. Zum Beispiel ist √2 irrational, aber nicht transzendent.

Die Nummer e

Die transzendente Zahl e ist die Basis natürlicher Logarithmen und ihre dezimale Approximation lautet:

e ≈ 2.718281828459045235360… .

Wenn Sie die Nummer schreiben wollten und genau, es wäre notwendig, unendliche Dezimalstellen zu schreiben, weil jede transzendente Zahl, wie bereits gesagt, irrational ist.

Die ersten zehn Ziffern von und sind leicht zu merken:

2,7 1828 1828 und obwohl es einem sich wiederholenden Muster zu folgen scheint, wird dies nicht in Dezimalstellen von mehr als neun erreicht.

Eine formellere Definition von und ist der nächste:

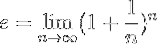
Was bedeutet, dass der genaue Wert von und wird erreicht, indem die in dieser Formel angegebene Operation ausgeführt wird, wenn die natürliche Zahl n neigt zur Unendlichkeit.

Dies erklärt, warum wir nur Annäherungen von erhalten können und, da egal wie groß die Zahl n ist, wird es immer möglich sein, a zu finden n höher.

Lassen Sie uns selbst nach Annäherungen suchen:

-Wenn n = 100, dann (1 + 1/100)¹⁰⁰ = 2.70481, was in der ersten Dezimalstelle kaum mit dem „wahren“ Wert von e übereinstimmt.

-Wenn Sie n = 10.000 wählen, haben Sie (1 + 1 / 10.000)^10.000 = 2.71815, was dem „exakten“ Wert von e in den ersten drei Dezimalstellen entspricht.

Dieser Prozess müsste unendlich verfolgt werden, um den "wahren" Wert von e zu erhalten. Ich glaube nicht, dass wir Zeit dafür haben, aber versuchen wir es noch einmal:

Verwenden wir n = 100.000:

(1 + 1 / 100.000)^100.000 = 2,7182682372

Das hat nur vier Dezimalstellen, die dem exakten Wert entsprechen.

Wichtig ist zu verstehen, dass je höher der Wert von n ist, der zur Berechnung von e gewählt wurde_n, Je näher es dem wahren Wert ist. Dieser wahre Wert wird jedoch nur dann erreicht, wenn n unendlich ist.

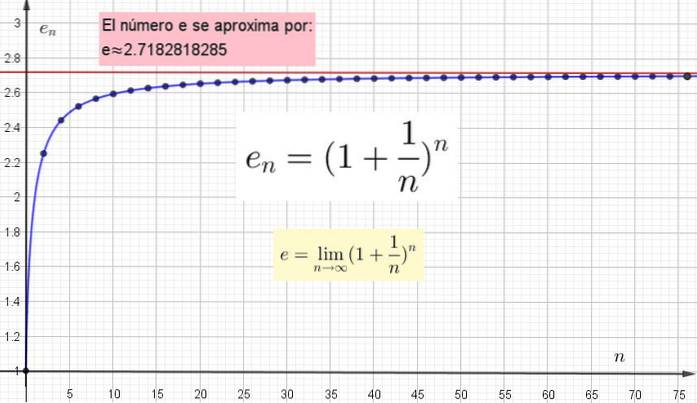
Andere wichtige Zahlen

Neben diesen berühmten Zahlen gibt es noch andere transzendente Zahlen, zum Beispiel:

- zwei^√2

Jede andere algebraische Zahl als 0 oder 1, die zu einem irrationalen Exponenten erhoben wird, ist eine transzendente Zahl.

-Die Champernowne-Nummer in Basis 10: 

C_10 = 0,123456789101112131415161718192021… .

-Die Champernowne-Nummer in Basis 2:

C_2 = 0.1101110010110111… .

-Die Gammazahl γ oder die Euler-Mascheroni-Konstante:

γ ≤ 0,577 215 664 901 532 860 606

Was durch die folgende Berechnung erhalten wird:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)

Wann n sei sehr sehr groß. Um den genauen Wert der Gammazahl zu erhalten, müssten Sie die Berechnung mit durchführen n unendlich. Ähnliches wie oben.

Und es gibt viel mehr transzendente Zahlen. Der große Mathematiker Georg Cantor, geboren in Russland und zwischen 1845 und 1918 lebend, zeigte, dass die Menge der transzendenten Zahlen viel größer ist als die Menge der algebraischen Zahlen.

Formeln, in denen die transzendente Zahl π erscheint

Der Umfang des Umfangs

P = π D = 2 π R, wobei P der Umfang, D der Durchmesser und R der Radius des Umfangs ist. Es sollte daran erinnert werden, dass:

-Der Durchmesser des Umfangs ist das längste Segment, das zwei Punkte desselben verbindet und das immer durch seine Mitte verläuft,

-Der Radius ist der halbe Durchmesser und das Segment, das von der Mitte zur Kante verläuft.

Fläche eines Kreises

A = π R.^zwei = ¼ π D.^zwei

Oberfläche einer Kugel

S = 4 π R.^zwei.

Ja. Obwohl es nicht so scheint, ist die Oberfläche einer Kugel dieselbe wie die von vier Kreisen mit demselben Radius wie die Kugel..

Volumen der Kugel

V = 4/3 π R.³

Ausbildung

- Übung 1

Die Pizzeria „EXÓTICA“ verkauft Pizzen mit drei Durchmessern: kleine 30 cm, mittlere 37 cm und große 45 cm. Ein Kind ist sehr hungrig und stellte fest, dass zwei kleine Pizzen genauso viel kosten wie eine große. Was ist besser für ihn, kaufen Sie zwei kleine oder eine große Pizza?

Lösung

Je größer die Fläche, desto größer die Menge an Pizza. Aus diesem Grund wird die Fläche einer großen Pizza berechnet und mit der von zwei kleinen Pizzen verglichen:

Großer Pizzabereich = ¼ π D.^zwei = ¼ ⋅ 3,1416⋅45^zwei = 1590,44 cm^zwei

Kleiner Pizzabereich = ¼ π d^zwei = ¼ ⋅ 3,1416⋅30^zwei = 706,86 cm^zwei

Daher haben zwei kleine Pizzen eine Fläche von 

2 x 706,86 = 1413,72 cm^zwei .

Es ist klar: Sie werden mehr Pizza haben, wenn Sie eine große als zwei kleine kaufen.

- Übung 2

Die Pizzeria „EXÓTICA“ verkauft auch eine halbkugelförmige Pizza mit einem Radius von 30 cm zum gleichen Preis wie eine rechteckige Pizza mit einer Seite von 30 x 40 cm. Welches würdest du nehmen?

Lösung

Wie im vorherigen Abschnitt erwähnt, ist die Oberfläche einer Kugel viermal so groß wie die eines Kreises mit demselben Durchmesser, sodass eine Halbkugel mit einem Durchmesser von 30 cm Folgendes aufweist:

12 '' halbkugelförmige Pizza: 1413,72 cm^zwei (zweimal ein Kreis mit dem gleichen Durchmesser)

Rechteckige Pizza: (30 cm) x (40 cm) = 1200 cm^zwei .

Die halbkugelförmige Pizza hat eine größere Fläche.

Verweise

1. Fernández J. Die Nummer e. Herkunft und Kuriositäten. Wiederhergestellt von: soymatematicas.com
2. Viel Spaß mit Mathe. Eulers Nummer. Wiederhergestellt von: gustolasmatematicas.com.
3. Figuera, J. 2000. Mathematik 1 .. Diversifiziert. CO-BO-Ausgaben.
4. García, M. Die Zahl e in der Elementarrechnung. Wiederhergestellt von: matematica.ciens.ucv.ve.
5. Wikipedia. PI-Nummer. Wiederhergestellt von: wikipedia.com
6. Wikipedia. Transzendente Zahlen. Wiederhergestellt von: wikipedia.com