
Eigenschaften, Beispiele, Übungen für zusammengesetzte Zahlen
Das zusammengesetzte Zahlen sind jene ganzen Zahlen, die mehr als zwei Teiler haben. Wenn wir genau hinschauen, sind alle Zahlen zumindest genau durch sich selbst und durch 1 teilbar. Diejenigen, die nur diese beiden Teiler haben, werden Primzahlen genannt, und diejenigen, die mehr haben, sind Verbindungen..
Schauen wir uns die Zahl 2 an, die nur zwischen 1 und 2 geteilt werden kann. Die Zahl 3 hat auch zwei Teiler: 1 und 3. Daher sind beide Primzahlen. Schauen wir uns nun die Zahl 12 an, die wir genau durch 2, 3, 4, 6 und 12 teilen können. Durch 5 Teiler ist 12 eine zusammengesetzte Zahl.
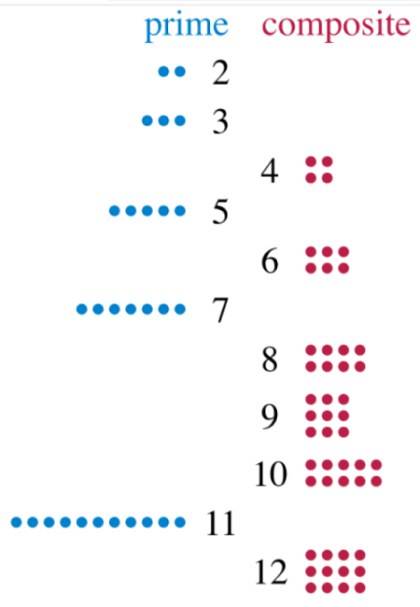
Und was passiert mit der Nummer 1, die alle anderen trennt? Nun, es ist keine Primzahl, weil es keine zwei Teiler hat und nicht zusammengesetzt ist, daher fällt 1 nicht in eine dieser beiden Kategorien. Aber es gibt noch viel mehr Zahlen..
Zusammengesetzte Zahlen können als Produkt von Primzahlen ausgedrückt werden, und dieses Produkt ist mit Ausnahme der Reihenfolge der Faktoren für jede Zahl eindeutig. Dies wird durch den Grundsatz der Arithmetik sichergestellt, den der griechische Mathematiker Euklid (325-365 v. Chr.) Bewiesen hat..
Kehren wir zu Nummer 12 zurück, die wir auf verschiedene Arten ausdrücken können. Probieren wir einige aus:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2zwei x 3 = 3 x 2zwei = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
Die fett hervorgehobenen Formen sind Produkte mit Primzahlen, und das einzige, was sich ändert, ist die Reihenfolge der Faktoren, von denen wir wissen, dass sie das Produkt nicht verändern. Die anderen Formen, obwohl gültig, um 12 auszudrücken, bestehen nicht nur aus Primzahlen.
Beispiele für zusammengesetzte Zahlen
Wenn wir eine zusammengesetzte Zahl in ihre Primfaktoren zerlegen wollen, müssen wir sie so zwischen Primzahlen aufteilen, dass die Division genau ist, dh dass der Rest 0 ist.
Diese Prozedur wird aufgerufen Primfaktorisierung oder kanonische Zerlegung. Primfaktoren können zu positiven Exponenten erhoben werden.
Wir werden die Zahl 570 zerlegen und dabei feststellen, dass sie gerade und daher durch 2 teilbar ist, was eine Primzahl ist.
Wir werden einen Schrägstrich verwenden, um die Zahl links von den Teilern rechts zu trennen. Die jeweiligen Quotienten werden unter die Zahl gestellt, sobald sie erhalten werden. Die Zerlegung ist abgeschlossen, wenn die letzte Zahl in der linken Spalte 1 ist:
570 │2
285 │
Wenn durch 2 geteilt wird, ist der Quotient 285, der durch 5 teilbar ist, eine weitere Primzahl, die mit 5 endet.
570 │2
285 5
57 │
57 ist teilbar durch 3, ebenfalls eine Primzahl, da die Summe seiner Ziffern 5 + 7 = 12 ein Vielfaches von 3 ist.
570 │2
285 5
57 3
19 │
Schließlich erhalten wir 19, eine Primzahl, deren Teiler 19 und 1 sind:
570 │2
285 5
57 3
19-19
1 │
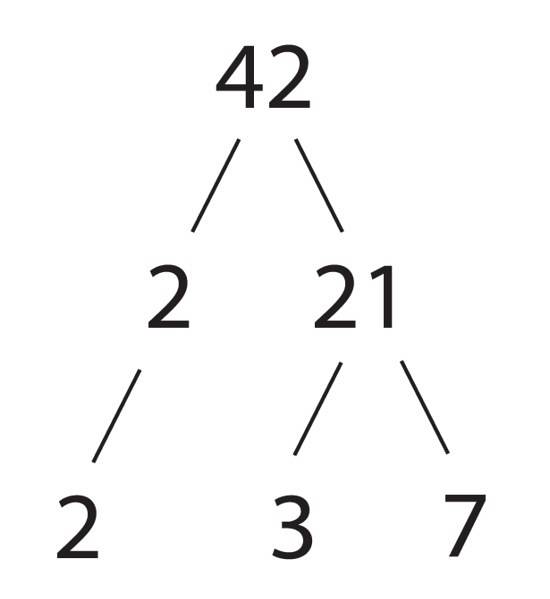
Wenn wir 1 erhalten, können wir bereits 570 folgendermaßen ausdrücken:
570 = 2 x 5 x 3 x 19
Und wir sehen, dass es tatsächlich das Produkt von 4 Primzahlen ist.
In diesem Beispiel beginnen wir mit der Division durch 2, aber die gleichen Faktoren (in einer anderen Reihenfolge) wären erhalten worden, wenn wir beispielsweise mit der Division durch 5 begonnen hätten.
Teilbarkeitskriterien
Um eine zusammengesetzte Zahl in ihre Primfaktoren zu zerlegen, muss sie genau geteilt werden. Die Kriterien für die Teilbarkeit zwischen Primzahlen sind Regeln, die es ermöglichen, zu wissen, wann eine Zahl durch eine andere genau teilbar ist, ohne es versuchen oder beweisen zu müssen.
-Teilbarkeit durch 2
Alle geraden Zahlen, die mit 0 oder einer geraden Zahl enden, sind durch 2 teilbar.
-Teilbarkeit durch 3
Wenn die Summe der Ziffern einer Zahl ein Vielfaches von 3 ist, ist die Zahl auch durch 3 teilbar.
-Teilbarkeit durch 5
Zahlen, die mit 0 oder 5 enden, sind durch 5 teilbar.
-Teilbarkeit durch 7
Eine Zahl ist durch 7 teilbar, wenn beim Trennen der letzten Ziffer, Multiplizieren mit 2 und Subtrahieren der verbleibenden Zahl der resultierende Wert ein Vielfaches von 7 ist.
Diese Regel scheint etwas komplizierter zu sein als die vorherigen, aber in Wirklichkeit ist es nicht so viel. Schauen wir uns also ein Beispiel an: wird 98 durch 7 teilbar sein?
Folgen wir den Anweisungen: Wir trennen die letzte Zahl, die 8 ist, multiplizieren sie mit 2, was 16 ergibt. Die Zahl, die beim Trennen der 8 verbleibt, ist 9. Wir subtrahieren 16 - 9 = 7. Und da 7 ein Vielfaches von sich selbst ist , 98 ist teilbar zwischen 7.
-Teilbarkeit durch 11
Wenn die Summe der Zahlen in gerader Position (2, 4, 6…) von der Summe der Zahlen in ungerader Position (1, 3, 5, 7…) subtrahiert wird und 0 oder ein Vielfaches von 11 erhalten wird, ergibt sich die Zahl ist teilbar durch 11.
Die ersten Vielfachen von 11 sind leicht zu identifizieren: Sie sind 11, 22, 33, 44… 99. Aber seien Sie vorsichtig, 111 ist nicht, stattdessen ist 110.
Lassen Sie uns als Beispiel sehen, ob 143 ein Vielfaches von 11 ist.
Diese Zahl hat 3 Ziffern, die einzige gerade Ziffer ist 4 (die zweite), die beiden ungeraden Ziffern sind 1 und 3 (erste und dritte) und ihre Summe ist 4.
Beide Summen werden subtrahiert: 4 - 4 = 0 und da 0 erhalten wird, stellt sich heraus, dass 143 ein Vielfaches von 11 ist.
-Teilbarkeit durch 13
Die Zahl ohne die Einerstelle muss vom 9-fachen dieser Ziffer abgezogen werden. Wenn die Zählung 0 oder ein Vielfaches von 13 zurückgibt, ist die Zahl ein Vielfaches von 13.
Als Beispiel werden wir überprüfen, ob 156 ein Vielfaches von 13 ist. Die Einerstelle ist 6 und die Zahl, die ohne sie bleibt, ist 15. Wir multiplizieren 6 x 9 = 54 und subtrahieren jetzt 54 - 15 = 39.
Aber 39 ist 3 x 13, also ist 56 ein Vielfaches von 13.
Primzahlen zueinander
Zwei oder mehr Primzahlen oder zusammengesetzte Zahlen können Primzahlen oder Co-Primzahlen sein. Dies bedeutet, dass der einzige gemeinsame Teiler, den sie haben, 1 ist.
Bei Koprimes sind zwei wichtige Eigenschaften zu beachten:
-Zwei, drei und mehr aufeinanderfolgende Zahlen sind immer Primzahlen zueinander.
-Das Gleiche gilt für zwei, drei oder mehr aufeinanderfolgende ungerade Zahlen.
Zum Beispiel sind 15, 16 und 17 Primzahlen zueinander, ebenso wie 15, 17 und 19.
Wie man weiß, wie viele Teiler eine zusammengesetzte Zahl hat
Eine Primzahl hat zwei Teiler, die gleiche Zahl und 1. Und wie viele Teiler hat eine zusammengesetzte Zahl? Dies können Cousins oder Verbindungen sein.
Sei N eine zusammengesetzte Zahl, ausgedrückt als kanonische Zerlegung wie folgt:
N = an . bm. cp... rk
Wobei a, b, c… r die Primfaktoren und n, m, p… k die jeweiligen Exponenten sind. Nun, die Anzahl der Teiler C, die N hat, ist gegeben durch:
C = (n + 1) (m + 1) (p + 1)… (k + 1)
Mit C = Primteiler + zusammengesetzte Teiler + 1
Zum Beispiel 570, was folgendermaßen ausgedrückt wird:
570 = 2 x 5 x 3 x 19
Alle Primfaktoren werden auf 1 erhöht, daher hat 570:
C = (1 + 1) (1 + 1) (1+ 1) (1 + 1) = 16 Teiler
Von diesen 10 Teilern kennen wir bereits: 1, 2, 3, 5, 19 und 570. Es fehlen 10 weitere Teiler, die zusammengesetzte Zahlen sind: 6, 10, 15, 30, 38, 57, 95, 114, 190 und 285. Sie werden gefunden, indem man die Zerlegung in Primfaktoren beobachtet und auch Kombinationen dieser Faktoren miteinander multipliziert..
Gelöste Übungen
- Übung 1
Zerlegen Sie die folgenden Zahlen in Primfaktoren:
a) 98
b) 143
c) 540
d) 3705
Lösung für
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
Lösung b
143 11
13-13
1 │
143 = 11 x 13
Lösung c
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2zwei x 33
Lösung d
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
- Übung 2
Finden Sie heraus, ob die folgenden Zahlen zueinander stehen:
6, 14, 9
Lösung
-Die Teiler von 6 sind: 1, 2, 3, 6
-Die 14 ist teilbar durch: 1, 2, 7, 14
-Schließlich hat 9 als Teiler: 1, 3, 9
Der einzige Teiler, den sie gemeinsam haben, ist 1, daher sind sie aufeinander abgestimmt.
Verweise
- Baldor, A. 1986. Arithmetik. Codex-Editionen und -Distributionen.
- Byjus. Primzahlen und zusammengesetzte Zahlen. Wiederhergestellt von: byjus.com.
- Primzahlen und zusammengesetzte Zahlen. Wiederhergestellt von: profeyennyvivaslapresentacion.files.wordpress.com
- Smartick. Teilbarkeitskriterien. Wiederhergestellt von: smartick.es.
- Wikipedia. Zusammengesetzte Zahlen. Wiederhergestellt von: en.wikipedia.org.

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.