
Froude Zahl, wie es berechnet wird und Beispiele
Das Froude Nummer In der Hydraulik gibt es die Beziehung an, die zwischen den Trägheitskräften und den Gravitationskräften für ein Fluid besteht. Daher ist es eine Möglichkeit, den folgenden Quotienten zu bezeichnen:

WoF. ist die Notation für die Froude-Nummer, eine dimensionslose Größe, die diesen Namen trägt, um den bemerkenswerten britischen Marinearchitekten und Wasserbauingenieur William Froude (1810-1879) zu ehren. Froude und sein Sohn experimentierten, indem sie flache Laken durch das Wasser zogen, um den Widerstand von Booten gegen Wellen abzuschätzen.

Bei der Einwirkung der Wellen, die ein Boot beim Segeln verursacht, oder der Strömung auf der Säule einer Brücke sind die Trägheits- und Schwerkraftkräfte vorhanden.
Die Froude-Zahl ist besonders wichtig für die Charakterisierung des Flüssigkeitsflusses in einem offenen Kanal. Ein offenes Rohr oder ein offener Kanal ist eine Leitung, deren Oberseite zur Atmosphäre hin offen ist. Beispiele gibt es in der Natur in Form von Flüssen und Bächen.
Und in künstlichen Konstruktionen haben wir:
-Dachrinnen und Abflüsse in Straßen und Gebäuden, um Regenwasser zu leiten.
-Gräben zur Bewässerung.
-Deponien und Abflüsse.
-Kühlkanäle für Industriemaschinen.
All dies sind Beispiele für Rohre, die zur Atmosphäre hin offen sind und bei denen die Froude-Zahl bei der Charakterisierung des Durchflusses immer berücksichtigt werden muss..
Artikelverzeichnis
- 1 Berechnung der Froude-Zahl
- 1.1 Froude-Nummer für ein offenes Rohr
- 2 Arten des Durchflusses gemäß der Froude-Nummer
- 2.1 Froude-Nummer und Reynolds-Nummer
- 3 Arbeitsbeispiel
- 3.1 Lösung
- 4 Referenzen
Berechnung der Froude-Zahl
Der zu Beginn angegebene Quotient zwischen den Trägheitskräften und denen der Schwerkraft nimmt in Abhängigkeit von den Parametern der Flüssigkeit folgende Form an:
Die vorherige Gleichung oder ihre Quadratwurzel ist die Froude-Zahl:

Froude-Nummer für ein offenes Rohr
Wie eingangs erläutert, ist der Wasserfluss durch Kanäle, die zur Atmosphäre hin offen sind, sehr häufig. In diesen Fällen erfolgt die Berechnung der Froude-Zahl nach folgender Formel:

N.F. = v / (gyh) ½
Wo Y.h ist die hydraulische Tiefe, v ist die mittlere Strömungsgeschwindigkeit und G ist der Wert der Erdbeschleunigung. Die hydraulische Tiefe wird wiederum wie folgt berechnet:
Y.h = A / T.
In dieser Formel stellt A die Nettoquerschnittsfläche dar und T ist die Breite der freien Oberfläche des Fluids, die der Atmosphäre ausgesetzt ist, am oberen Ende des Kanals oder Rohrs. Es gilt für einen rechteckigen Kanal oder einen Kanal, der breit genug und mit konstanter Tiefe ist.
Es ist wichtig hervorzuheben, dass das Produkt, da NF dimensionslos ist, das Produkt ist gyh es muss das Quadrat einer Geschwindigkeit sein. In der Tat kann gezeigt werden, dass:
coderzwei = gyh
Mit coder als Ausbreitungsgeschwindigkeit einer Oberflächenwelle, analog zur Schallgeschwindigkeit in einer Flüssigkeit. Daher ist die Froude-Zahl auch analog zur Mach-Zahl, die häufig verwendet wird, um die Geschwindigkeit von Flugzeugen mit der von Schall zu vergleichen..
Flusstypen gemäß der Froude-Nummer
Der Flüssigkeitsstrom in einem offenen Kanal wird gemäß dem Wert von N in drei Bereiche eingeteiltF.::
-Wenn nF. < 1, se tiene un movimiento en régimen lento o unterkritisch.
-OhneF. = 1 Der Fluss wird benannt kritischer Fluss.
-Schließlich, wenn Sie N habenF. > 1 Die Bewegung erfolgt schnell oder überkritisch.
Froude-Nummer und Reynolds-Nummer
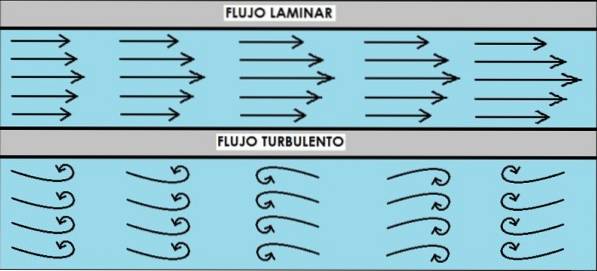
Reynolds Nummer N.R. ist eine weitere dimensionslose Größe, die für die Analyse des Flüssigkeitsflusses sehr wichtig ist und anhand derer bekannt ist, wann sich die Flüssigkeit verhält laminieren und wann ist es turbulent. Diese Konzepte gelten sowohl für geschlossene als auch für offene Kanalströme..
Eine Strömung ist laminar, wenn sich die Flüssigkeit in Schichten, die sich nicht vermischen, gleichmäßig und geordnet bewegt. Andererseits ist die turbulente Strömung dadurch gekennzeichnet, dass sie chaotisch und ungeordnet ist.
Eine Möglichkeit, herauszufinden, ob ein Wasserfluss laminar oder turbulent ist, besteht darin, einen Tintenstrom einzuspritzen. Wenn die Strömung laminar ist, fließt der Tintenstrom getrennt von der des Wassers. Wenn es sich jedoch um eine turbulente Strömung handelt, mischt sich die Tinte und löst sich schnell im Wasser auf.

In diesem Sinne haben wir, wenn wir die Effekte der Froude-Zahl mit denen der Reynolds-Zahl kombinieren:
-Unterkritisch laminar: N.R. < 500 y NF. < 1
-Turbulent unterkritisch: N.R. > 2000 und N.F. < 1
-Überkritisches Laminar: N.R. < 500 y NF. > 1
-Überkritisch turbulent: N.R. > 2000 und N.F. > 1
Wenn die Strömungen in den Übergangsbereichen auftreten, ist es aufgrund ihrer Instabilität schwieriger, sie zu charakterisieren.
Gearbeitetes Beispiel
Ein 4 m breiter und 1 m tiefer Fluss fließt 3 m3 / s. Stellen Sie fest, ob der Fluss unterkritisch oder überkritisch ist.
Lösung
Um den Wert von N zu findenF. Es ist erforderlich, die Geschwindigkeit der Flussströmung zu kennen. Die Aussage gibt uns den Durchfluss, auch Volumenstrom genannt, der von der Querschnittsfläche und der Geschwindigkeit v des Durchflusses abhängt. Es wird wie folgt berechnet:
Q = A.v.
Wo Q. ist der Fluss, ZU ist die Querschnittsfläche und v ist die Geschwindigkeit. Angenommen, eine rechteckige Querschnittsfläche:
A = Breite x Tiefe = 4 m x 1 m = 4 mzwei
Dann ist die Geschwindigkeit v:
v = Q / A = 3 m3 / s / 4 mzwei= 0,75 m / s
Die hydraulische Tiefe im Fall des Rohrs mit rechteckigem Querschnitt stimmt mit der Tiefe überein, weshalb N durch Werte in der Gleichung ersetzt wirdF., mit Y.h = 1 m Y. g = 9,8 m / szwei du hast:
N.F. = v / (gyh) ½ = 0,75 m / s / (9,8 m / szwei x 1 m) ½ = 0,24
Da N.F. kleiner als 1 ist, hat der Fluss ein unterkritisches Verhalten, dh langsam.
Verweise
- Cimbala, C. 2006. Strömungsmechanik, Grundlagen und Anwendungen. Mc. Graw Hill.
- Franzini, J. 1999. Strömungsmechanik mit Anwendung ist in Engineering. Mc. Graw Hill.
- Mott, R. 2006. Fluid Mechanics. 4 .. Auflage. Pearson Ausbildung.
- White, F. 2004. Fluid Mechanics. 5. Auflage. Mc Graw Hill.
- Wikipedia. Froude Nummer. Wiederhergestellt von: es.wikipedia.org.

Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.