
Winkel in den Umfangstypen, Eigenschaften, gelösten Übungen
Namens Umfangswinkel diejenigen, in denen sich einige seiner Elemente an einem bestimmten Umfang befinden oder schneiden. Unter ihnen sind die folgenden:
1.- Die zentraler Winkel, dessen Scheitelpunkt in der Mitte des Umfangs liegt und dessen Seiten ihm gegenüber sekant sind, wie wir im folgenden Bild sehen:

2.- Die Beschriftungswinkel, deren Scheitelpunkt am Umfang liegt und dessen Seiten am Umfang sekant oder tangential sind.
3.- Außenwinkel, deren Scheitelpunkt außerhalb des Umfangs liegt, dessen Seiten jedoch am Umfang sekant oder tangential sind.
4.- Die Innenwinkel, mit dem Scheitelpunkt innerhalb des Umfangs und seinen daran befestigten Seiten.
Alle diese Winkel haben bestimmte Beziehungen zueinander und dies führt uns zu wichtigen Eigenschaften zwischen den Winkeln, die zu einem bestimmten Kreis gehören.
Artikelverzeichnis
- 1 Eigenschaften
- 1.1 - Zentralwinkel
- 1.2 - Beschriftungswinkel
- 1.3 - Außenwinkel
- 1.4 - Innenwinkel
- 2 Gelöste Übungen
- 2.1 - Übung 1
- 2.2 - Übung 2
- 3 Referenzen
Eigenschaften
- Zentralwinkel
Der zentrale Winkel ist definiert als derjenige, dessen Scheitelpunkt in der Mitte des Umfangs liegt und dessen Seiten den Umfang schneiden.
Das Maß im Bogenmaß eines zentralen Winkels ist der Quotient zwischen dem Teilbogen, dh dem Umfangsbogen zwischen den Seiten des Winkels, und dem Radius des Umfangs.
Wenn der Umfang einheitlich ist, dh den Radius 1 hat, ist das Maß für den zentralen Winkel die Länge des Bogens, die der Anzahl der Bogenmaß entspricht.
Wenn Sie das Maß des Zentralwinkels in Grad wünschen, multiplizieren Sie das Maß im Bogenmaß mit dem Faktor 180º / π.
Winkelmessgeräte wie der Winkelmesser und das Goniometer verwenden immer einen zentralen Winkel und die Länge des Nebenbogens.
Sie sind in sexagesimalen Graden kalibriert, was bedeutet, dass bei jeder Messung eines Winkels im Hintergrund die Länge des Bogens gemessen wird, der vom zentralen Winkel begrenzt wird.
Eigentum
Das Maß für einen zentralen Winkel im Bogenmaß ist gleich der Länge des Teil- oder Schnittbogens geteilt durch die Länge des Radius.
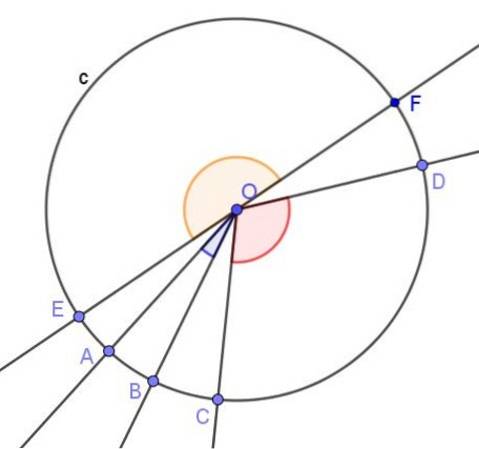
- Beschrifteter Winkel
Der Beschriftungswinkel eines Kreises ist einer, dessen Scheitelpunkt am Umfang liegt und dessen Strahlen sekant oder tangential zu ihm sind..
Seine Eigenschaften sind:
Eigenschaften
-Der Beschriftungswinkel ist konvex oder eben.
-Wenn ein beschrifteter Winkel denselben Bogen wie der zentrale Winkel schneidet, ist das Maß des ersten Winkels halb so groß wie das des zweiten..
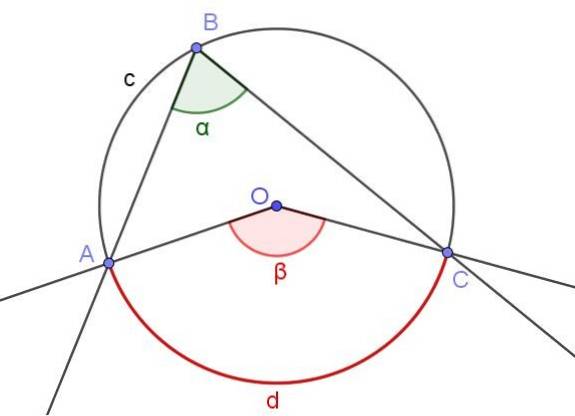
Abbildung 3 zeigt zwei Winkel ∠ABC und ∠AOC, die denselben Umfangsbogen A⌒C schneiden.
Wenn das Maß des Beschriftungswinkels α ist, ist das Maß β des Zentralwinkels doppelt so groß wie das Maß des Beschriftungswinkels (β = 2 α), da beide den gleichen Maßbogen d bilden.
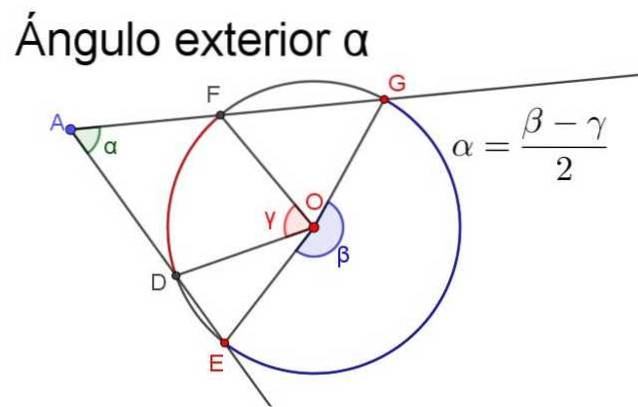
- Außenwinkel
Es ist der Winkel, dessen Scheitelpunkt außerhalb des Umfangs liegt und dessen Seiten den Umfang an einem oder mehreren Punkten schneiden.
Eigentum
-Sein Maß ist gleich der halben Differenz (oder Differenz geteilt durch 2) der zentralen Winkel, die dieselben Bögen abfangen.
Um sicherzustellen, dass die Messung positiv ist, muss die Halbdifferenz immer die des größten Mittelwinkels minus der Messung des kleinsten Mittelwinkels sein, wie in der folgenden Abbildung dargestellt.
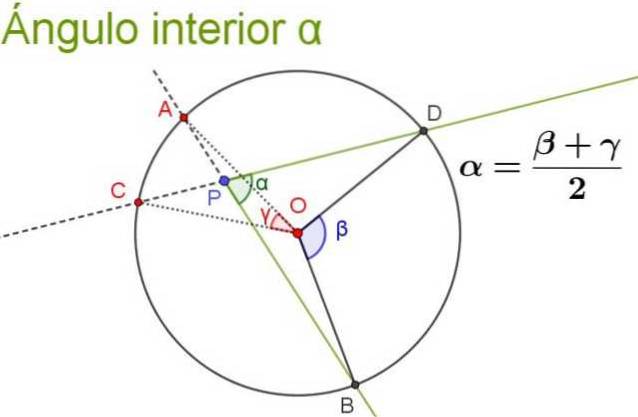
- Innenwinkel
Der Innenwinkel ist derjenige, dessen Scheitelpunkt innerhalb des Umfangs liegt und dessen Seiten den Umfang schneiden.
Eigentum
Sein Maß ist gleich der Halbwertsumme des Mittelwinkels, der denselben Bogen begrenzt, plus des Mittelwinkels, der denselben Bogen wie sein Ausdehnungswinkel begrenzt (dies ist der Innenwinkel, der durch die Strahlen gebildet wird, die zu denen des ursprünglichen Innenwinkels komplementär sind ).
Die folgende Abbildung veranschaulicht und verdeutlicht die Eigenschaft des Innenwinkels.
Gelöste Übungen
- Übung 1
Angenommen, ein Beschriftungswinkel, in dem eine seiner Seiten durch den Mittelpunkt des Kreises verläuft, wie in Abbildung 6 gezeigt. Der Radius des Kreises beträgt OA = 3 cm und der Bogen d hat eine Länge von π / 2 cm. Bestimmen Sie den Wert der Winkel α und β.
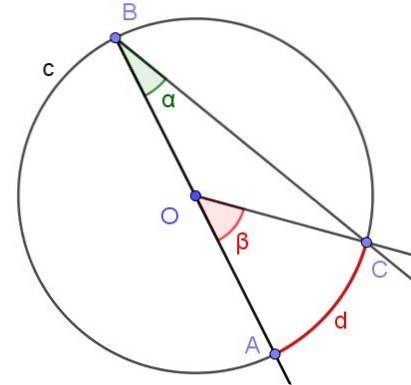
Lösung
In diesem Fall wird das gleichschenklige Dreieck COB gebildet, da [OC] = [OB]. In einem gleichschenkligen Dreieck sind die Winkel neben der Basis gleich, daher ist ∠BCO = ∠ABC = α. Andererseits ist ∠COB = 180º - β. Betrachtet man die Summe der Innenwinkel des Dreiecks COB, so ergibt sich:
α + α + (180º - β) = 180º
Daraus folgt, dass 2 & agr; = & bgr; oder was äquivalent ist & agr; = & bgr; / 2, womit die Eigenschaft (3) des vorherigen Abschnitts bestätigt wird, dass das Maß des Beschriftungswinkels die Hälfte des Mittelwinkels ist, wenn beide Winkel den gleichen Akkord einfügen [AC].
Nun fahren wir mit der Bestimmung der numerischen Werte fort: Der Winkel β ist zentral und sein Maß im Bogenmaß ist der Quotient zwischen dem Bogen d und dem Radius r = OA, also ist sein Maß:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.
Andererseits wurde bereits festgestellt, dass α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Übung 2
In Abbildung 7 sind die Winkel α1 und βzwei Sie haben das gleiche Maß. Weiterhin ist der Winkel β1 misst 60º. Bestimmen Sie die Winkel β und α.
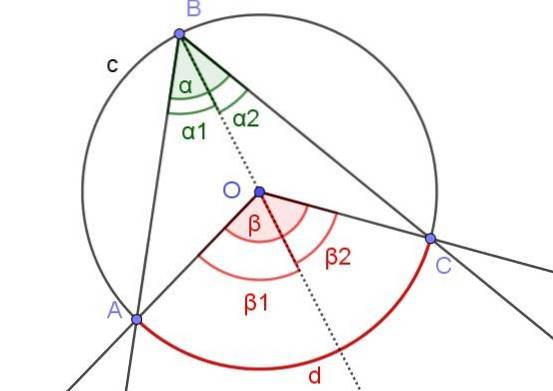
Lösung
In diesem Fall haben wir einen beschrifteten Winkel ∠ABC, in dem der Mittelpunkt O des Umfangs innerhalb des Winkels liegt.
Aufgrund der Eigenschaft (3) haben wir αzwei = βzwei / 2 und α1 = β1 /zwei. Was:
α = α1 + αzwei und β = β1 + βzwei
Daraus folgt:
α = α1 + αzwei = β1 / 2 + βzwei / 2 = (β1 + βzwei) / 2 = β / 2.
Das heißt, entsprechend den Eigenschaften:
α = β / 2
Da wird uns gesagt, dass β1 = 60º dann:
α1 = β1 / 2 = 60º / 2 = 30º.
Sie sagen uns auch, dass α1 = βzwei Daraus folgt:
βzwei = 30º.
Der Winkel β ergibt:
β1 + βzwei = 60º + 30º = 90º.
Und da α = β / 2 ist, dann:
α = 90º / 2 = 45º.
Abschließend:
β = 90º und α = 45º.
Verweise
- Baldor, A. 1973. Geometrie und Trigonometrie. Zentralamerikanischer Kulturverlag.
- E. A. 2003. Elemente der Geometrie: mit Übungen und Kompassgeometrie. Universität von Medellin.
- Geometrie 1. ESO. Winkel am Umfang. Wiederhergestellt von: edu.xunta.es.
- Alle Wissenschaft. Gelöste Winkelprobleme im Umfang gelöst. Wiederhergestellt von: francesphysics.blogspot.com
- Wikipedia. Beschrifteter Winkel. Wiederhergestellt von: es.wikipedia.com


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.