
Komplementäre Winkel, welche und wie sie berechnet werden, Beispiele, Übungen

Zwei oder mehr Winkel sind ergänzende Winkel wenn die Summe seiner Messungen der eines rechten Winkels entspricht. Bekanntlich beträgt das Maß für einen rechten Winkel in Grad 90º und im Bogenmaß π / 2.
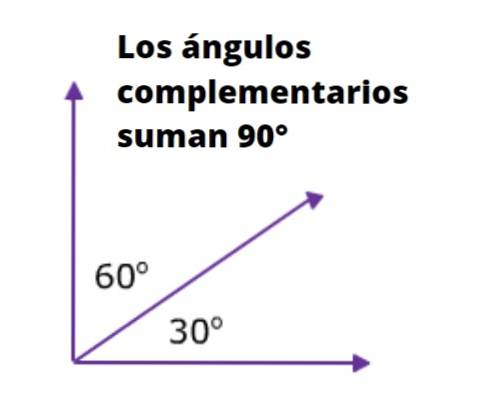
Zum Beispiel sind die beiden Winkel neben der Hypotenuse eines rechtwinkligen Dreiecks komplementär zueinander, da die Summe ihrer Maße 90º beträgt. Die folgende Abbildung ist in dieser Hinsicht sehr anschaulich:
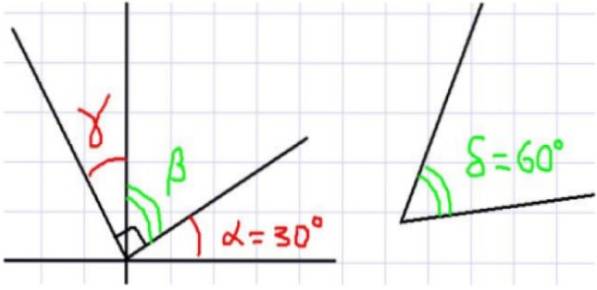
In Abbildung 1 sind insgesamt vier Winkel dargestellt. α und β sind komplementär, da sie es sind benachbart und ihre Summe vervollständigt einen rechten Winkel. In ähnlicher Weise ist β komplementär zu γ, woraus folgt, dass γ und α gleich groß sind.
Da nun die Summe von α und δ gleich 90 Grad ist, kann festgestellt werden, dass α und δ komplementär sind. Da außerdem β und δ das gleiche komplementäre α haben, kann festgestellt werden, dass β und δ das gleiche Maß haben.
Artikelverzeichnis
- 1 Beispiele für komplementäre Winkel
- 1.1 - Beispiele A, B und C.
- 1.2 - Beispiele D, E und F.
- 2 Übungen
- 2.1 - Übung 1
- 2.2 - Übung 2
- 2.3 - Übung 3
- 3 Winkel senkrechter Seiten
- 3.1 Allgemeine Regel für senkrechte Seitenwinkel
- 4 Referenzen
Beispiele für komplementäre Winkel
In den folgenden Beispielen wird darum gebeten, die unbekannten Winkel zu finden, die in Abbildung 2 mit Fragezeichen markiert sind.
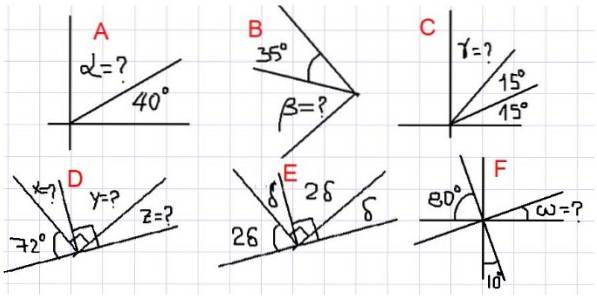
- Beispiele A, B und C.
Die folgenden Beispiele sind in der Reihenfolge ihrer Komplexität aufgeführt.
Beispiel A.
In der obigen Abbildung haben wir, dass sich die benachbarten Winkel α und 40º zu einem rechten Winkel addieren. Das heißt, α + 40º = 90º, daher α = 90º - 40º = 50º.
Beispiel B.
Da β zum Winkel von 35º komplementär ist, ist β = 90º - 35º = 55º.
Beispiel C.
Aus Abbildung 2C ergibt sich die Summe von γ + 15º + 15º = 90º. Mit anderen Worten ist γ komplementär zum Winkel 30º = 15º + 15º. So dass:
γ = 90º - 30º = 60º
- Beispiele D, E und F.
In diesen Beispielen sind mehr Winkel beteiligt. Um die Unbekannten zu finden, muss der Leser das Konzept des komplementären Winkels so oft wie nötig anwenden.
Beispiel D.
Da X zu 72º komplementär ist, folgt X = 90º - 72º = 18º. Außerdem ist Y komplementär zu X, also Y = 90º - 18º = 72º.
Schließlich ist Z komplementär zu Y. Aus all dem folgt, dass:
Z = 90º - 72º = 18º
Beispiel E.
Die Winkel δ und 2δ sind komplementär, daher ist δ + 2δ = 90º.
Das heißt, 3δ = 90º, was impliziert, dass δ = 90º / 3 = 30º ist.
Beispiel F.
Wenn wir den Winkel zwischen ω und 10º U nennen, dann ist U zu beiden ergänzend, weil beobachtet wird, dass ihre Summe einen rechten Winkel vervollständigt. Daraus folgt, dass U = 80º. Da U zu ω komplementär ist, ist ω = 10º.
Ausbildung
Im Folgenden werden drei Übungen vorgeschlagen. In allen muss der Wert der Winkel A und B in Grad gefunden werden, damit die in Abbildung 3 gezeigten Beziehungen erfüllt sind.
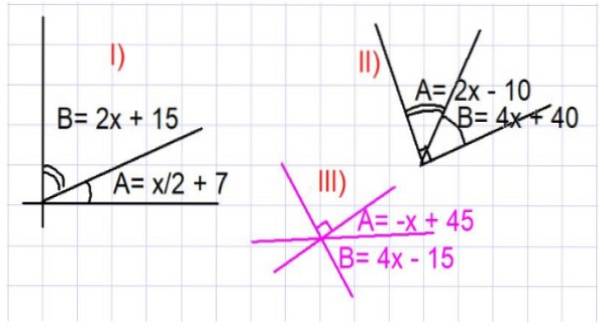
- Übung 1
Bestimmen Sie die Werte der Winkel A und B aus Teil I) von Abbildung 3.
Lösung
Aus der gezeigten Figur ist ersichtlich, dass A und B komplementär sind, daher A + B = 90º. Wir ersetzen den Ausdruck für A und B als Funktion von x in Teil I):
(x / 2 + 7) + (2x + 15) = 90
Dann werden die Terme entsprechend gruppiert und eine einfache lineare Gleichung wird erhalten:
(5x / 2) + 22 = 90
Wenn wir 22 in beiden Mitgliedern abziehen, haben wir:
5x / 2 = 90-22 = 68
Und schließlich wird der Wert von x gelöscht:
x = 2 * 68/5 = 136/5
Nun wird der Winkel A durch Ersetzen des Wertes von X gefunden:
A = (136/5) / 2 +7 = 103/5 = 20,6 º.
Während Winkel B ist:
B = 2 · 136/5 + 15 = 347/5º = 69,4º .
- Übung 2
Finden Sie die Werte der Winkel A und B von Bild II, Abbildung 3.
Lösung
Da A und B komplementäre Winkel sind, haben wir wieder: A + B = 90º. Wenn wir den Ausdruck für A und B als Funktion von x ersetzen, der in Teil II) von 3 angegeben ist, haben wir:
(2x - 10) + (4x +40) = 90
Gleiche Begriffe werden zusammengefasst, um die folgende Gleichung zu erhalten:
6 x + 30 = 90
Wenn Sie beide Mitglieder durch 6 teilen, erhalten Sie:
x + 5 = 15
Daraus folgt, dass x = 10º.
Deshalb:
A = 2 · 10 & supmin; ¹ & sup0; = 10º
B = 4 · 10 + 40 = 80º.
- Übung 3
Bestimmen Sie die Werte der Winkel A und B aus Teil III) von Abbildung 3.
Lösung
Wieder wird die Figur sorgfältig analysiert, um die komplementären Winkel zu finden. In diesem Fall haben wir A + B = 90 Grad. Wenn wir den in der Abbildung angegebenen Ausdruck für A und B als Funktion von x einsetzen, haben wir:
(-x +45) + (4x -15) = 90
3 x + 30 = 90
Das Teilen beider Mitglieder durch 3 ergibt Folgendes:
x + 10 = 30
Daraus folgt, dass x = 20º.
Mit anderen Worten ist der Winkel A = -20 +45 = 25º. Und seinerseits: B = 4 * 20 -15 = 65º.
Senkrechte Seitenwinkel
Zwei Winkel sollen sein senkrechte Seiten wenn jede Seite ihre entsprechende Senkrechte auf der anderen hat. Die folgende Abbildung verdeutlicht das Konzept:
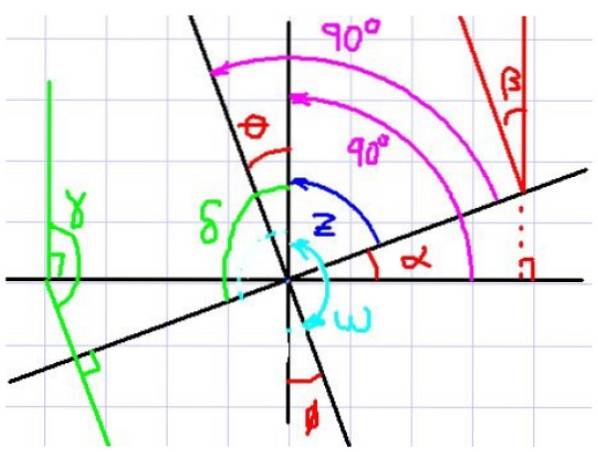
In 4 sind zum Beispiel die Winkel & agr; und & thgr; beobachtet. Beachten Sie nun, dass jeder Winkel seine entsprechende Senkrechte zum anderen Winkel hat.
Es ist auch zu sehen, dass α und θ den gleichen komplementären Winkel haben z, Daher kommt der Beobachter sofort zu dem Schluss, dass α und θ das gleiche Maß haben. Es scheint dann, dass wenn zwei Winkel Seiten senkrecht zueinander haben, sie gleich sind, aber schauen wir uns einen anderen Fall an.
Betrachten Sie nun die Winkel α und ω. Diese beiden Winkel haben ebenfalls entsprechende senkrechte Seiten, es kann jedoch nicht gesagt werden, dass sie gleich groß sind, da einer spitz und der andere stumpf ist..
Man beachte, dass ω + θ = 180º ist. Weiterhin ist θ = α. Wenn Sie diesen Ausdruck für z in der ersten Gleichung einsetzen, erhalten Sie:
δ + α = 180º, wobei δ und α zueinander senkrechte Seitenwinkel sind.
Faustregel für Winkel senkrechter Seiten
Aus dem Vorgenannten kann eine Regel aufgestellt werden, die erfüllt ist, solange die Winkel senkrechte Seiten haben:
Wenn zwei Winkel zueinander senkrechte Seiten haben, sind sie gleich, wenn beide spitz oder beide stumpf sind. Andernfalls, wenn einer akut und der andere stumpf ist, sind sie ergänzend, dh sie addieren sich zu 180º.
Wenn wir diese Regel anwenden und uns auf die Winkel in Abbildung 4 beziehen, können wir Folgendes bestätigen:
α = β = θ = φ
γ = δ
Mit dem Zusatzwinkel ω von α, β, θ und φ.
Verweise
- Baldor, J. A. 1973. Ebenen- und Raumgeometrie. Zentralamerikanisches Kultur.
- Mathematische Gesetze und Formeln. Winkelmesssysteme. Wiederhergestellt von: ingemecanica.com.
- Wentworth, G. Flugzeuggeometrie. Wiederhergestellt von: gutenberg.org.
- Wikipedia. Ergänzende Winkel. Wiederhergestellt von: es.wikipedia.com
- Wikipedia. Förderer. Wiederhergestellt von: es.wikipedia.com
- Zapata F. Goniómetro: Geschichte, Teile, Betrieb. Wiederhergestellt von: lifeder.com


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.