
Beispiele für Parallelogrammmethoden, gelöste Übungen
Das Parallelogrammmethode ist eine grafische Methode zum Hinzufügen von zwei Vektoren in der Ebene. Es wird häufig verwendet, um das Ergebnis von zwei auf einen Körper ausgeübten Kräften oder von zwei Geschwindigkeiten zu ermitteln, wie im Fall eines Schwimmers, der beabsichtigt, einen Fluss senkrecht zu überqueren und von der Strömung abgelenkt wird.
Um das Parallelogramm zu erstellen, müssen die Ursprünge der hinzuzufügenden, maßstabsgetreuen Vektoren an einem Punkt zusammenfallen.
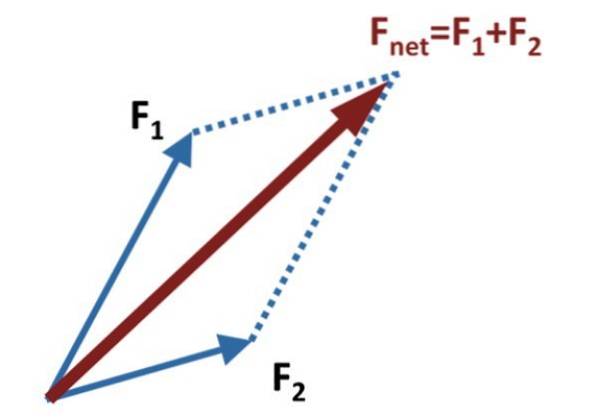
Dann werden Hilfslinien parallel zu jedem Vektor gezeichnet und erreichen das Ende des anderen, wie in der obigen Abbildung gezeigt.
Die Summe oder der resultierende Vektor, auch Nettokraft genannt, ist der Vektor F.Netz, Dies wird durch Zeichnen des Vektors erhalten, der vom gemeinsamen Ursprung von ausgeht F.1 Y. F.zwei, bis zu dem Punkt, an dem sich die parallelen Hilfslinien schneiden. Im Diagramm der Figur sind diese durch gepunktete Linien dargestellt.
Die Methode hat ihren Namen von der Figur, die mit den Addend-Vektoren und den Hilfslinien gebildet wird, was genau ein Parallelogramm ist. Die Hauptdiagonale des Parallelogramms ist der Summenvektor.
Es ist sehr wichtig zu beachten, dass die Reihenfolge, in der die Additionsvektoren platziert werden, die Summe überhaupt nicht ändert, da diese Operation zwischen Vektoren kommutativ ist.
Artikelverzeichnis
- 1 Beispiel für die Parallelogrammmethode Schritt für Schritt
- 1.1 Sonderfall: Summe der senkrechten Vektoren
- 2 Gelöste Übungen
- 2.1 - Übung 1
- 2.2 - Übung 2
- 3 Referenzen
Beispiel für die Parallelogrammmethode Schritt für Schritt
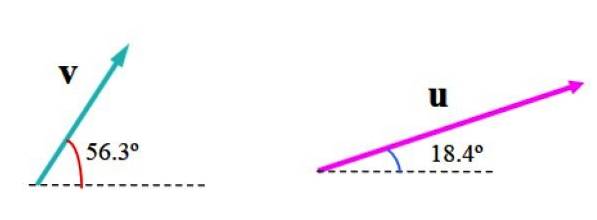
Das folgende Bild zeigt die Vektoren v Y. oder in beliebigen Einheiten. Der Vektor v misst 3,61 Einheiten und bildet mit der Horizontalen einen Winkel von 56,3º, während oder misst 6,32 Einheiten und einen Winkel von 18,4º in Bezug auf die Referenzlinie.
Wir werden seine Vektorsumme mit der Parallelogrammmethode ermitteln.
Wählen Sie einen geeigneten Maßstab, wie den in der folgenden Abbildung gezeigten, in dem die Ebene durch ein Raster geteilt wurde. Die Breite des Quadrats entspricht einer (1) Einheit.
Da die Vektoren bei der Übersetzung nicht verändert werden, werden sie so positioniert, dass ihre Ursprünge mit dem Ursprung des Koordinatensystems übereinstimmen (Bild links)..
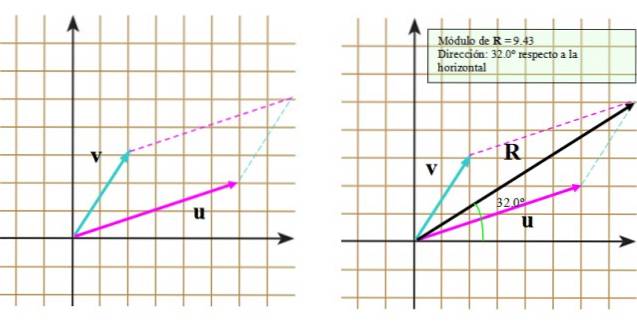
Befolgen wir nun diese Schritte:
- Zeichnen Sie bis zum Ende des Vektors v eine segmentierte Linie, die parallel zum Vektor ist oder.
- Wiederholen Sie den Vorgang, diesmal jedoch mit dem Ende des Vektors oder.
- Zeichnen Sie die Hauptdiagonale vom gemeinsamen Ursprung bis zum Schnittpunkt der segmentierten Linien.
Das Ergebnis ist im rechten Bild zu sehen, in dem der resultierende Vektor erscheint R..
Wenn wir die Größe von wissen wollen R., Wir können seine Länge messen und ihn mit der Skala vergleichen, die wir haben. In Bezug auf die Richtung kann beispielsweise die horizontale oder die vertikale Achse als Referenz verwendet werden.
Bei Verwendung der horizontalen Achse oder der x-Achse der Winkel, der R. Die Form mit dieser Achse wird mit dem Winkelmesser gemessen und auf diese Weise kennen wir die Richtung von R..
Ebenso die Größe und Richtung von R. kann unter Verwendung der Kosinus- und Sinussätze berechnet werden, da das gebildete Parallelogramm in zwei kongruente Dreiecke unterteilt werden kann, deren Seiten die Module der Vektoren sind oder, v Y. R.. Siehe Arbeitsbeispiel 1.
Sonderfall: Summe der senkrechten Vektoren
Wenn die Vektoren senkrecht zueinander stehen, ist die gebildete Figur ein Rechteck. Der Modul des resultierenden Vektors entspricht der Länge der Diagonale, die mit dem Satz von Pythagoras leicht berechnet werden kann.
Gelöste Übungen
- Übung 1
Wir haben den Vektor v, Das misst 3,61 Einheiten und bildet mit der Horizontalen und dem Vektor einen Winkel von 56,3º oder, Das Maß beträgt 6,32 Einheiten und bildet einen Winkel von 18,4 ° (Abbildung 2). Bestimmen Sie den Modul des resultierenden Vektors R. = oder + v und die Richtung, die der Vektor mit der horizontalen Achse bildet.
Lösung
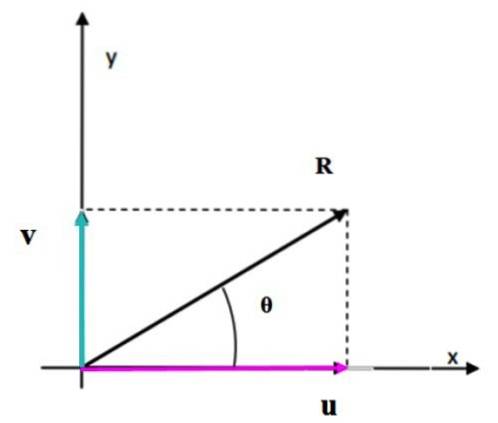
Das Parallelogrammverfahren wird gemäß den oben beschriebenen Schritten angewendet, um den Vektor zu erhalten R.. Wie zuvor gesagt, wenn die Vektoren sorgfältig gezeichnet werden, indem man der Skala folgt und das Lineal und den Winkelmesser verwendet, die Größe und Richtung von R. werden direkt auf der Zeichnung gemessen.
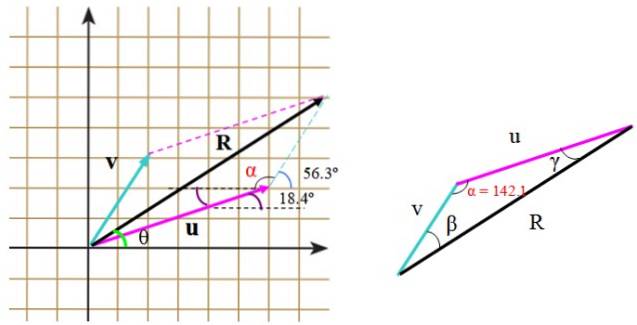
Sie können auch direkt mit Hilfe der Trigonometrie und der Eigenschaften von Winkeln berechnet werden. Wenn das gebildete Dreieck nicht richtig ist, wie in diesem Fall, wird der Kosinussatz angewendet, um die fehlende Seite zu finden.
Im Dreieck rechts messen die Seiten u, v und R. Um den Kosinussatz anzuwenden, muss der Winkel zwischen bekannt sein v Y. oder, dass wir mit Hilfe des Gitters finden können, die Winkel, die durch die Aussage bereitgestellt werden, angemessen zu positionieren.
Dieser Winkel ist α und setzt sich zusammen aus:
α = (90-56,3º) + 90º + 18,4º = 142,1º
Nach dem Kosinussatz:
R.zwei = vzwei + oderzwei - 2u⋅v⋅cos α = 3,61zwei + 6.32zwei - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 Einheiten.
Schließlich ist der Winkel zwischen R. und die horizontale Achse ist θ = 18,4 º + γ. Der Winkel γ kann mit dem Sinussatz ermittelt werden:
sin α / R = sin γ / u
Deshalb:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6º
θ = 18,4º + 13,6º = 32º
- Übung 2
Ein Schwimmer ist dabei, einen senkrecht zur Strömung schwimmenden Fluss mit einer konstanten Geschwindigkeit von 2,0 m / s zu überqueren. Der Schwimmer startet von A, endet jedoch aufgrund des Stroms, der ihn umgeleitet hat, bei B, einem Punkt stromabwärts.
Wenn die Geschwindigkeit der Strömung 0,8 m / s beträgt und alle Geschwindigkeiten als konstant angenommen werden, ermitteln Sie die Geschwindigkeit des Schwimmers, wie sie von einem am Ufer stehenden Beobachter gesehen wird.
Lösung
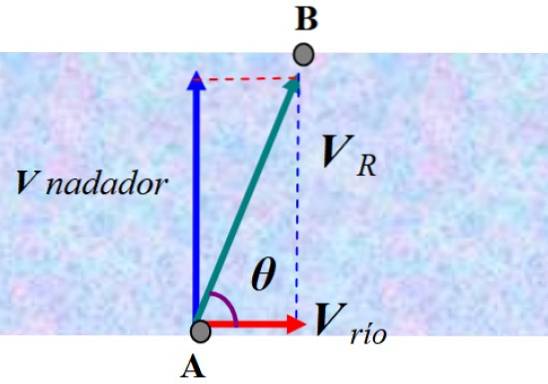
Ein Beobachter, der am Ufer steht, würde sehen, wie der Schwimmer entsprechend der resultierenden Geschwindigkeit abgelenkt wird V.R.. Um die Antwort zu finden, müssen wir die Geschwindigkeit des Schwimmers in Bezug auf das Wasser und die Geschwindigkeit der Strömung, die wir nennen, vektoriell addieren V. Fluss::
V. R. = V. Schwimmer + V. Fluss
In der Figur, die nicht maßstabsgetreu ist, wurden die Vektoren addiert, um zu erhalten V. R.. In diesem Fall kann der Satz von Pythagoras angewendet werden, um seine Größe zu erhalten:
V.R.zwei = 2,0zwei + 0,8zwei = 4,64
V.R. = 2,15 m / s
Die Richtung, in der der Schwimmer von der senkrechten Richtung abweicht, lässt sich leicht berechnen, wobei Folgendes zu beachten ist:
θ = arctg (2 / 0,8) = 68,2º
Dann weicht der Schwimmer um 90º - 68,2º = 27,2º von seiner ursprünglichen Richtung ab.
Verweise
- Bauer, W. 2011. Physik für Ingenieurwissenschaften. Band 1. Mc Graw Hill.
- Bedford, 2000. A. Technische Mechanik: Statik. Addison Wesley.
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 1. Kinematik. Herausgegeben von Douglas Figueroa (USB).
- Giambattista, A. 2010. Physik. 2 .. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitätsphysik mit moderner Physik. 14 .. Ed. Band 1.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.