
Pendelbewegung
Was ist die Pendelbewegung??
Das Pendelbewegung Es ist eine Hin- und Herbewegung, die von einem mehr oder weniger schweren Gegenstand ausgeführt wird, der als Pendel bezeichnet wird und an einem Seil oder einer leichten Stange aufgehängt ist und an seinem anderen Ende befestigt ist.
Das Pendel erhält einen Anfangsimpuls und darf schwingen, so beschreibt das Objekt Bögen hin und her. Dies ist das Prinzip, wie Pendeluhren, Schaukeln, Schaukelstühle und Metronome Pendel, verwendet, um die Zeiten in der Musik zu markieren.
Es wird gesagt, dass Galileo Galilei um 1581 die Schwingung einer Lampe in der Kathedrale von Pisa beobachtete und beobachtete, dass, obwohl die Schwingungsamplitude des Kandelabers aufgrund der Reibung mit der Luft abnahm, nicht die Dauer des Lampenzyklus.
Dies erregte die Aufmerksamkeit von Galileo, der sich entschied, mit der Studie fortzufahren und feststellte, dass die Periode des Pendels nicht von der Masse abhängt, sondern von der Quadratwurzel der Länge des Akkords, wie später zu sehen sein wird..
Pendelbewegungseigenschaften
Ein Pendel ist sehr einfach zu bauen, da es ausreicht, wenn eine Lotschnur an einem Baumwollfaden hängt und mit den Fingern am anderen Ende gehalten oder wie ein Nagel an einer Stütze befestigt wird..
Nach dem kleinen Anfangsimpuls ist das Gewicht dafür verantwortlich, das Pendel in Schwingung zu halten, obwohl die Reibung die Amplitude der Bewegung verringert, bis es schließlich vollständig aufhört..
Das Hauptmerkmal der Pendelbewegung ist die Wiederholung, da es sich um eine Hin- und Herbewegung handelt. Um das Studium zu erleichtern, ist es nun zweckmäßig, einige Vereinfachungen vorzunehmen, um sich auf ein einfacheres Modell zu konzentrieren, das als das bezeichnet wird einfaches Pendel.
Das einfache Pendel

Es ist ein ideales System, das aus einer Lotlinie besteht, die als Punktmasse betrachtet wird m, befestigt an einem leichten, nicht dehnbaren Seil der Länge L.. Die Eigenschaften dieses Systems sind:
- Haben Sie eine sich wiederholende und periodische Bewegung, die darin besteht, einen Umfangsbogen mit einem Radius von L hin und her zu bewegen.
- Berücksichtigt keine Reibung.
- Der Bewegungsbereich ist klein (< 5º).
- Die Periode ist unabhängig von der Masse m, und hängt ausschließlich von der Länge ab L. Pendel.
Formeln und Gleichungen
Das Folgende ist ein Diagramm des einfachen Pendels, auf das zwei Kräfte wirken: das Gewicht P. der Größe mg, die vertikal nach unten gerichtet ist und die Spannung T. Am Seil. Reibung wird nicht berücksichtigt.
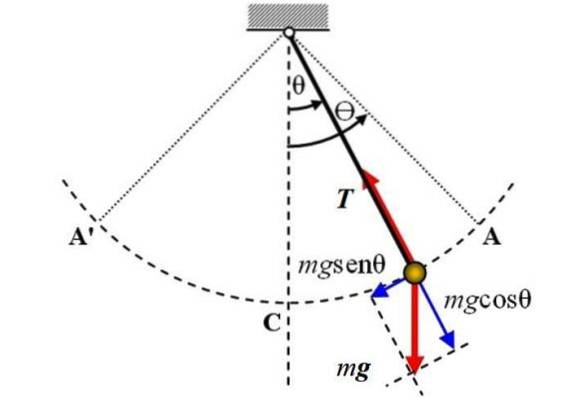
Die Referenzachse ist die vertikale Achse und fällt mit der Position θ = 0 zusammen. Von dort wird die Winkelverschiebung θ entweder in die eine oder andere Richtung gemessen. Das + -Zeichen kann der rechten Verschiebung in der Abbildung zugeordnet werden.
Um die Bewegung des Pendels zu untersuchen, wird ein Koordinatensystem mit dem Ursprung am Pendel selbst gewählt. Dieses System hat eine Tangentialkoordinate zum vom Pendel beschriebenen Umfangsbogen A'CA sowie eine Radialkoordinate, die auf die Mitte der Flugbahn gerichtet ist..
In dem in der Abbildung gezeigten Moment bewegt sich das Pendel nach rechts, aber die tangentiale Schwerkraftkomponente, die als F bezeichnet wirdt, ist dafür verantwortlich, dass er zurückkommt. Aus der Figur ist ersichtlich, dass diese Komponente der Bewegungsrichtung entgegengesetzt ist.
In Bezug auf die Spannung im Seil wird es mit der Komponente des Gewichts mgcosθ ausgeglichen.

Winkelverschiebung
Wir müssen die Gleichung in Form einer einzelnen Variablen ausdrücken und uns daran erinnern, dass die Winkelverschiebung θ und der zurückgelegte Bogen durch die folgende Gleichung zusammenhängen:
s = L.θ
Die Masse hebt sich auf beiden Seiten auf und wenn die Amplitude klein ist, auch der Winkel θ, so dass die folgende Annäherung gültig ist:
sen θ ≈ θ
Damit wird die folgende Differentialgleichung für die Variable θ (t) erhalten:


Diese Gleichung ist sehr einfach zu lösen, da ihre Lösung eine Funktion ist, deren zweite Ableitung die Funktion selbst ist. Es gibt drei Alternativen: einen Cosinus, einen Sinus oder einen Exponentialwert. Die Kosinusfunktion wird für die Winkelverschiebung θ (t) gewählt, da es sich um eine bekannte und einfach zu handhabende Funktion handelt.
Der Leser kann durch zweimaliges Differenzieren überprüfen, ob die folgende Funktion die Differentialgleichung erfüllt:
θ (t) = θm cos (ωt + φ)
Wo θm ist der maximale Winkel, um den sich das Pendel in Bezug auf die Vertikale bewegt, und die Winkelfrequenz ω ist:

Gleichung der Periode
Die Periode T der Bewegung ist die Zeit, die zum Ausführen eines Zyklus benötigt wird, und ist definiert als:

Einsetzen von ω:

Wie oben erwähnt, hängt die Periode nicht von der Masse des Pendels ab, sondern nur von seiner Länge..
Beispiele für Pendelbewegungen
Herzfrequenzmessung
Galileo hatte die Idee, die Herzfrequenz von Menschen zu messen und die Länge des Pendels so anzupassen, dass die Periode mit den Herzschlägen einer Person übereinstimmt.
Die Pendeluhr
Dies ist zweifellos eines der bekanntesten Beispiele für Pendelbewegungen. Bei der Herstellung von Pendeluhren geht es sowohl um Wissenschaft als auch um Kunst. Der niederländische Physiker Christian Huygens (1629-1695) entwickelte 1656 die erste Pendeluhr, basierend auf der vor Jahren von Galileo durchgeführten Studie.
Foucaults Pendel

Es ist ein etwas anderes Pendel als das oben beschriebene, da es sich in jeder vertikalen Ebene drehen kann. Es wurde vom französischen Physiker Léon Foucault (1819-1868) geschaffen und dient zur Visualisierung der Erdrotation.
Übung gelöst
Ein einfaches Pendel fährt alle 0,5 s durch die Gleichgewichtsposition. Wie lang ist der Faden??
Lösung
Da die Periode die Zeit ist, die benötigt wird, um einen vollständigen Zyklus abzuschließen, in dem er die Gleichgewichtsposition zweimal durchläuft: einer geht und der andere zurück, dann:
T = 2 × 0,5 s = 1 s
Von:

Die Länge L des Fadens wird gelöscht:

Der Faden ist 0,25 m oder 25 cm lang.
Verweise
- Figueroa, D. (2005). Reihe: Physik für Wissenschaft und Technik. Band 2. Dynamik. Herausgegeben von Douglas Figueroa (USB).
- Giambattista, A. 2010. Physik. 2 .. Ed. McGraw Hill.
- Giancoli, D. 2006. Physik: Prinzipien mit Anwendungen. 6 .. Ed Lehrlingshalle.
- Katz, D. 2013. Physik für Wissenschaftler und Ingenieure. Grundlagen und Verbindungen. Lernen einbinden.
- Knight, R. 2017. Physik für Wissenschaftler und Ingenieure: ein strategischer Ansatz. Pearson.



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.