Das Drehmoment, Drehmoment oder Moment einer Kraft ist die Fähigkeit einer Kraft, eine Drehung zu verursachen. Etymologisch erhält es den Namen Drehmoment als Ableitung des englischen Wortes Drehmoment, aus dem Lateinischen torquere (Twist).
Das Drehmoment (in Bezug auf einen bestimmten Punkt) ist die physikalische Größe, die sich aus der Herstellung des Vektorprodukts zwischen den Positionsvektoren des Punktes, an dem die Kraft ausgeübt wird, und dem der ausgeübten Kraft (in der angegebenen Reihenfolge) ergibt. Dieser Moment hängt von drei Hauptelementen ab.
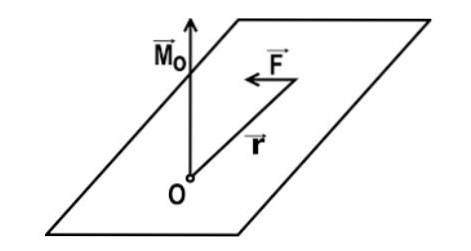
Das erste dieser Elemente ist die Größe der ausgeübten Kraft, das zweite ist der Abstand zwischen dem Punkt, an dem sie angewendet wird, und dem Punkt, um den sich der Körper dreht (auch als Hebelarm bezeichnet), und das dritte Element ist der Winkel der Anwendung dieser Kraft.
Je größer die Kraft, desto größer der Spin. Das gleiche passiert mit dem Hebelarm: Je größer der Abstand zwischen dem Punkt, an dem die Kraft ausgeübt wird, und dem Punkt, in Bezug auf den sie die Drehung erzeugt, desto größer ist dieser Abstand.
Natürlich ist das Drehmoment für Bau und Industrie von besonderem Interesse, und es ist in unzähligen Anwendungen für den Haushalt vorhanden, beispielsweise wenn eine Mutter mit einem Schraubenschlüssel angezogen wird..
Artikelverzeichnis
Der mathematische Ausdruck des Drehmoments einer Kraft in Bezug auf einen Punkt O ist gegeben durch: M = r x F.
In diesem Ausdruck ist r der Vektor, der den Punkt von O mit dem Punkt P der Kraftanwendung verbindet, und F ist der Vektor der ausgeübten Kraft.
Die Maßeinheiten des Moments sind N ∙ m, die zwar dem Joule (J) dimensional äquivalent sind, aber eine andere Bedeutung haben und nicht verwechselt werden sollten.
Daher nimmt der Modul des Drehmoments den Wert an, der durch den folgenden Ausdruck gegeben ist:
M = r ≤ F ≤ sin α
In diesem Ausdruck ist α der Winkel zwischen dem Kraftvektor und dem Vektor r oder dem Hebelarm. Das Drehmoment gilt als positiv, wenn sich der Körper gegen den Uhrzeigersinn dreht. im Gegenteil, es ist negativ, wenn es sich im Uhrzeigersinn dreht.
Wie bereits oben erwähnt, ergibt sich die Maßeinheit des Drehmoments aus dem Produkt einer Krafteinheit und einer Abstandseinheit. Insbesondere verwendet das Internationale Einheitensystem das Newtonmeter, dessen Symbol N • m ist.
Auf einer Dimensionsebene scheint das Newtonmeter dem Joule äquivalent zu sein; Der Juli sollte jedoch in keinem Fall verwendet werden, um Momente auszudrücken. Das Joule ist eine Einheit zum Messen von Werken oder Energien, die sich konzeptionell stark von Torsionsmomenten unterscheiden.
In gleicher Weise hat das Torsionsmoment einen Vektorcharakter, der sowohl die Skalararbeit als auch die Energie ist.
Aus dem Gesehenen folgt, dass das Drehmoment einer Kraft in Bezug auf einen Punkt die Fähigkeit einer Kraft oder eines Satzes von Kräften darstellt, die Drehung des Körpers um eine Achse zu modifizieren, die durch den Punkt verläuft..
Daher erzeugt das Torsionsmoment eine Winkelbeschleunigung am Körper und ist eine Größe eines Vektorzeichens (so wird es aus einem Modul, einer Richtung und einem Sinn definiert), das in den Mechanismen vorhanden ist, die einer Torsion oder Biegung ausgesetzt wurden.
Das Drehmoment ist Null, wenn der Kraftvektor und der Vektor r die gleiche Richtung haben, da in diesem Fall der Wert von sin α Null ist.
Bei einem bestimmten Körper, auf den eine Reihe von Kräften wirkt, ergibt sich das Drehmoment, das sich aus der Anwendung all dieser Kräfte ergibt, wenn die ausgeübten Kräfte in derselben Ebene wirken. ist die Summe der Torsionsmomente, die sich aus jeder Kraft ergeben. Daher ist es wahr, dass:
M.T. = ∑ M = M.1 + M.zwei + M.3 +...
Natürlich ist es notwendig, das Vorzeichenkriterium für Torsionsmomente zu berücksichtigen, wie oben erläutert.
Das Drehmoment ist in alltäglichen Anwendungen wie dem Festziehen einer Mutter mit einem Schraubenschlüssel oder dem Öffnen oder Schließen eines Hahns oder einer Tür vorhanden.
Seine Anwendungen gehen jedoch viel weiter; Das Drehmoment findet sich auch in den Achsen der Maschine oder im Ergebnis der Anstrengungen, denen die Träger ausgesetzt sind. Daher sind seine Anwendungen in Industrie und Mechanik vielfältig..
Im Folgenden finden Sie einige Übungen, um das Verständnis der oben genannten Punkte zu erleichtern.
In der folgenden Abbildung, in der die Abstände zwischen Punkt O und den Punkten A und B 10 cm bzw. 20 cm betragen:
a) Berechnen Sie den Wert des Drehmomentmoduls in Bezug auf Punkt O, wenn am Punkt A eine Kraft von 20 N ausgeübt wird.
b) Berechnen Sie den Wert der in B ausgeübten Kraft, um das gleiche Drehmoment wie im vorherigen Abschnitt zu erzielen.
Erstens ist es zweckmäßig, die Daten in Einheiten des internationalen Systems zu übertragen.
rZU = 0,1 m
rB. = 0,2 m
a) Um den Modul des Drehmoments zu berechnen, verwenden wir die folgende Formel:
M = r ≤ F ≤ sin α = 0,1 ≤ 20 ≤ 1 = 2 N ≤ m
b) Um die angeforderte Streitmacht zu bestimmen, gehen Sie wie folgt vor:
M = r ≤ F ≤ sin α = 0,2 ≤ F ≤ 1 = 2 N ≤ m
Durch Auflösen nach F wird erhalten, dass:
F = 10 N.
Eine Frau übt am Ende eines 30 cm langen Schraubenschlüssels eine Kraft von 20 N aus. Wenn der Kraftwinkel mit dem Schraubenschlüsselgriff 30 ° beträgt, wie hoch ist das Drehmoment auf die Mutter??
Die folgende Formel wird angewendet und die Operation wird ausgeführt:
M = r ≤ F ≤ sin α = 0,3 ≤ 20 ≤ 0,5 = 3 N ≤ m
Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.