
Messungen von Position, zentraler Tendenz und Streuung
Das Messungen der zentralen Tendenz, Streuung und Position, sind Werte, die verwendet werden, um einen Satz statistischer Daten richtig zu interpretieren. Diese können direkt bearbeitet werden, wie sie aus der statistischen Studie stammen, oder sie können in Gruppen gleicher Häufigkeit organisiert werden, um die Analyse zu erleichtern..
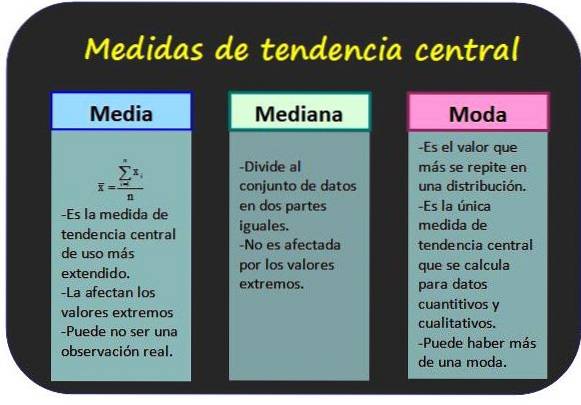
Maße der zentralen Tendenz
Sie ermöglichen es zu wissen, um welche Werte die statistischen Daten gruppiert sind.
Arithmetischer Durchschnitt
Sie wird auch als Durchschnitt der Werte einer Variablen bezeichnet und erhalten Sie, indem Sie alle Werte addieren und das Ergebnis durch die Gesamtzahl der Daten dividieren.
-
Arithmetisches Mittel für nicht gruppierte Daten
Sei eine Variable x, von der wir n Daten haben, ohne sie zu organisieren oder zu gruppieren, so wird ihr arithmetisches Mittel wie folgt berechnet:

Und in Summationsnotation:

Beispiel
Die Besitzer eines Bergtouristengasthauses haben die Absicht zu wissen, wie viele Tage die Besucher durchschnittlich in den Einrichtungen bleiben. Zu diesem Zweck wurde eine Aufzeichnung der Tage der Beständigkeit von 20 Gruppen von Touristen geführt, wobei die folgenden Daten erhalten wurden:
1; 1; zwei; zwei; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; zwei; zwei; 3; 4; 1
Die durchschnittliche Anzahl der Tage, an denen Touristen bleiben, beträgt:

-
Arithmetisches Mittel für gruppierte Daten
Wenn die Daten der Variablen in einer Tabelle der absoluten Frequenzen f organisiert sindich und die Klassenzentren sind x1, xzwei,..., xn, Der Mittelwert wird berechnet durch:

In Summationsnotation:

Median
Der Median einer Gruppe von n Werten der Variablen x ist der zentrale Wert der Gruppe, sofern die Werte in aufsteigender Reihenfolge angeordnet sind. Auf diese Weise ist die Hälfte aller Werte kleiner als der Modus und die andere Hälfte größer..
-
Median der nicht gruppierten Daten
Folgende Fälle können auftreten:
-Anzahl n der Werte der Variablen x seltsam: Der Median ist der Wert, der genau in der Mitte der Wertegruppe liegt:

-Anzahl n der Werte der Variablen x Paar: In diesem Fall wird der Median als Durchschnitt der beiden zentralen Werte der Datengruppe berechnet:

Beispiel
Um den Median der Daten aus der Touristenherberge zu ermitteln, werden diese zuerst vom niedrigsten zum höchsten geordnet:
1; 1; 1; 1; 1; 1; 1; zwei; zwei; zwei;; zwei;; 3; 3; 3; 4; 4; 4; 4; 5; 5
Die Anzahl der Daten ist gerade, daher gibt es zwei zentrale Daten: X.10 und X.elf und da beide 2 wert sind, ist auch ihr Durchschnitt.
Median = 2
-
Median der gepoolten Daten
Die folgende Formel wird verwendet:

Die Symbole in der Formel bedeuten:
-c: Breite des Intervalls, das den Median enthält
-B.M.: Untergrenze des gleichen Intervalls
-F.m: Anzahl der Beobachtungen in dem Intervall, zu dem der Median gehört.
-n: Gesamtdaten.
-F.BM: Anzahl der Beobachtungen Vor des Intervalls, das den Median enthält.
Mode
Der Modus für nicht gruppierte Daten ist der Wert mit der höchsten Frequenz, während er für gruppierte Daten die Klasse mit der höchsten Frequenz ist. Mode gilt als die repräsentativsten Daten oder Klassen der Distribution.
Zwei wichtige Merkmale dieser Maßnahme sind, dass ein Datensatz mehr als einen Modus haben kann und der Modus sowohl für quantitative als auch für qualitative Daten bestimmt werden kann..
Beispiel
Wenn man mit den Daten des Touristenparadors fortfährt, ist diejenige, die am häufigsten wiederholt wird, 1, daher ist es am üblichsten, dass Touristen 1 Tag im Parador bleiben.
Dispersionsmaße
Dispersionsmaße beschreiben, wie gruppiert die Daten um die zentralen Maße sind.
Rang
Sie wird berechnet, indem die größten und die kleinsten Daten subtrahiert werden. Wenn dieser Unterschied groß ist, ist dies ein Zeichen dafür, dass die Daten gestreut sind, während kleine Werte anzeigen, dass die Daten nahe am Mittelwert liegen..
Beispiel
Der Bereich für die Daten des Touristenparadors ist:
Bereich = 5-1 = 4
Varianz
-
Varianz für nicht gruppierte Daten
Um die Varianz zu finden szwei Es ist erforderlich, zuerst das arithmetische Mittel zu kennen, dann die quadratische Differenz zwischen jedem Datenelement und dem Mittelwert zu berechnen. Alle werden addiert und durch die Gesamtzahl der Beobachtungen geteilt. Diese Unterschiede sind bekannt als Abweichungen.

Die Varianz, die immer positiv (oder Null) ist, gibt an, wie weit die Beobachtungen vom Mittelwert entfernt sind: Wenn die Varianz hoch ist, sind die Werte stärker verteilt als wenn die Varianz klein ist.
Beispiel
Die Abweichung für die Daten aus der Touristenherberge beträgt:
1; 1; zwei; zwei; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; zwei; zwei; 3; 4; 1

-
Varianz für gruppierte Daten
Um die Varianz eines gruppierten Datensatzes zu ermitteln, ist Folgendes erforderlich: i) der Mittelwert, ii) die Frequenz fich Dies sind die Gesamtdaten in jeder Klasse und iii) xich oder Klassenwert:

Die Standardabweichung ist die positive Quadratwurzel der Varianz, hat also einen Vorteil gegenüber der Varianz: Sie wird in denselben Einheiten wie die untersuchte Variable angegeben, sodass Sie eine direktere Vorstellung davon haben, wie nah oder fern die Variable ist vom Durchschnitt.
-
Standardabweichung für nicht gruppierte Daten
Es wird einfach durch Finden der Quadratwurzel der Varianz für nicht gruppierte Daten bestimmt:

Die Standardabweichung für die Daten von der Touristenherberge beträgt:
s = √ (szwei) = √ 1,95 = 1,40
-
Standardabweichung für gruppierte Daten
Sie wird berechnet, indem die Quadratwurzel der Varianz für gruppierte Daten ermittelt wird:

Positionsmessungen
Positionsmessungen teilen einen geordneten Datensatz in gleich große Teile. Der Median ist nicht nur ein Maß für die zentrale Tendenz, sondern auch ein Maß für die Position, da er das Ganze in zwei gleiche Teile teilt. Kleinere Teile können jedoch mit Quartilen, Dezilen und Perzentilen erhalten werden.
Quartile
Die Quartile teilen die Menge in vier gleiche Teile, die jeweils 25% der Daten enthalten. Sie werden als Q bezeichnet1, Q.zwei und Q.3 und der Median ist das Quartil Q.zwei. Auf diese Weise liegen 25% der Daten unterhalb des Q-Quartils.1, 50% unter dem Q-Quartilzwei oder Median und 75% unter dem Q-Quartil3.

-
Quartile für nicht gruppierte Daten
Die Daten werden geordnet und die Summe in 4 Gruppen mit jeweils der gleichen Anzahl von Daten unterteilt. Die Position des ersten Quartils ergibt sich aus:
Q.1 = (n + 1) / 4
Wobei n die Gesamtdaten sind. Wenn das Ergebnis eine ganze Zahl ist, befinden sich die Daten, die dieser Position entsprechen, aber wenn sie dezimal sind, werden die Daten, die dem ganzzahligen Teil entsprechen, mit dem nächsten gemittelt oder für eine größere Genauigkeit werden sie linear zwischen diesen Daten interpoliert.
Beispiel
Die Position des ersten Quartils Q.1 Für die Daten des Touristenparadors gilt:
Q.1 = (n + 1) / 4 = (20 + 1) / 4 = 5,25
Dies ist die Position von Quartil 1, und da das Ergebnis dezimal ist, werden die Daten X durchsucht5 und X.6, welche sind jeweils X.5 = 1 und X.6 = 1 und werden gemittelt, was ergibt:
Erstes Quartil = 1
1; 1; 1; 1; 1;; 1;; 1; zwei; zwei;; zwei; zwei; 3; 3; 3; 4; 4; 4; 4; 5; 5.
Die Position des zweiten Quartils Q.zwei es ist:
Q.zwei = 2 (n + 1) / 4 = 10,5
Was ist der Durchschnitt zwischen X.10 und X.elf und entspricht dem Median:
Zweites Quartil = Median = 2
Die Position des dritten Quartils wird berechnet durch:
Q.3 = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75
Es ist auch dezimal, daher wird X gemitteltfünfzehn und X.16::
1; 1; 1; 1; 1; 1; 1; zwei; zwei;; zwei; zwei; 3; 3; 3; 4;; 4;; 4; 4; 5; 5.
Aber da beide 4 wert sind:
Drittes Quartil = 4
Die allgemeine Formel für die Position von Quartilen in nicht gruppierten Daten lautet:
Q.k = k (n + 1) / 4
Mit k = 1,2,3.
-
Quartile für gruppierte Daten
Sie werden ähnlich wie der Median berechnet:

Die Erklärung der Symbole lautet:
-B.Q.: untere Grenze des Intervalls, das das Quartil enthält
-c: Breite dieses Intervalls
-F.Was: Anzahl der im Quartilintervall enthaltenen Beobachtungen.
-n: Gesamtdaten.
-F.BQ: Anzahl der Daten Vor des Intervalls, das das Quartil enthält.
Dezile und Perzentile
Die Dezile und Perzentile teilen den Datensatz in 10 gleiche Teile bzw. 100 gleiche Teile, und ihre Berechnung erfolgt auf ähnliche Weise wie die der Quartile.
-
Dezile und Perzentile für nicht gruppierte Daten
Die Formeln werden jeweils verwendet:
D.k = k (n + 1) / 10
Mit k = 1,2,3… 9.
Dezil D.5 muss gleich dem Median sein.
P.k = k (n + 1) / 100
Mit k = 1,2,3… 99.
Das P-Perzentilfünfzig muss gleich dem Median sein.
Beispiel
Im Beispiel der Touristenherberge ist die Position des D.3 es ist:
D.3 = 3 (20 + 1) / 10 = 6,3
Da es sich um eine Dezimalzahl handelt, wird X gemittelt6 und X.7, beide gleich 1:
1; 1; 1; 1; 1; 1;; 1;; zwei; zwei; zwei; zwei; 3; 3; 3; 4; 4; 4; 4; 5; 5
Dies bedeutet, dass 3 Zehntel der Daten unter X liegen7 = 1 und die restlichen oben.
-
Dezile und Perzentile für gruppierte Daten
Die Formeln sind analog zu denen für Quartile. D wird verwendet, um Dezile und P für Perzentile zu bezeichnen, und die Symbole werden ähnlich interpretiert:

Die empirische Regel
Wenn die Daten symmetrisch verteilt sind und die Verteilung unimodal ist, wird eine Regel aufgerufen empirische Regel oder Regel 68 - 95 - 99, das gruppiert sie in den folgenden Intervallen:
- 68% der Daten liegen im Bereich:

- 95% der Daten liegen im Bereich:

- 99% der Daten liegen im Bereich:

Beispiel
In welchem Intervall sind 95% der Daten vom Touristenparador?
Sie liegen im Intervall: [2.5−1.40; 2,5 + 1,40] = [1,1; 3.9].
Verweise
- Berenson, M. 1985. Statistik für Management und Wirtschaft. Interamericana S.A..
- Devore, J. 2012. Wahrscheinlichkeit und Statistik für Ingenieurwesen und Wissenschaft. 8 .. Auflage. Engagieren.
- Levin, R. 1988. Statistik für Administratoren. 2 .. Auflage. Prentice Halle.
- Spiegel, M. 2009. Statistik. Schaum-Serie. 4 .. Auflage. Mcgraw Hügel.
- Walpole, R. 2007. Wahrscheinlichkeit und Statistik für Ingenieurwissenschaften und Naturwissenschaften. Pearson.


Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.