
Molmasse, wie man sie berechnet, Beispiele und gelöste Übungen
Das Molmasse ist eine intensive Eigenschaft der Materie, die das Konzept eines Maulwurfs mit Massenmessungen in Beziehung setzt. Genauer gesagt ist es die Massenmenge, die einem Mol Substanz entspricht; das heißt, was eine Avogadro-Nummer „wiegt“ (6.022 · 10)2. 3) von bestimmten Partikeln.
Ein Mol einer Substanz enthält die gleiche Anzahl von Partikeln (Ionen, Moleküle, Atome usw.). Seine Masse wird jedoch variieren, da seine molekularen Dimensionen durch die Anzahl der Atome und die Isotope definiert sind, aus denen seine Struktur besteht. Je massereicher das Atom oder Molekül ist, desto größer ist seine Molmasse..
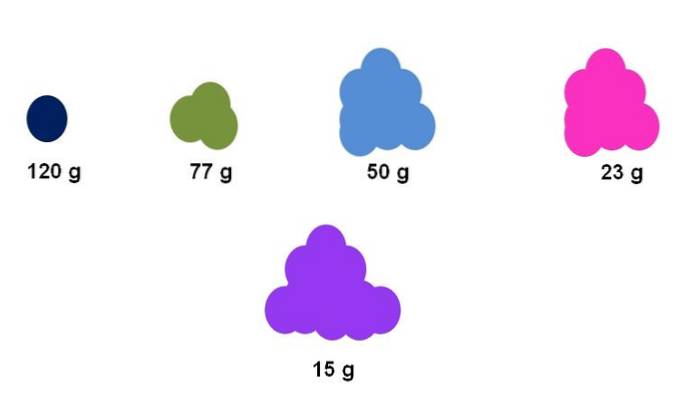
Angenommen, für fünf verschiedene Verbindungen wird genau ein Mol gesammelt (oberes Bild). Unter Verwendung einer Waage wurde die Masse für jeden Cluster, wie unten ausgedrückt, gemessen. Diese Masse entspricht der Molmasse. Von allen hat die violette Verbindung die leichtesten Partikel, während die dunkelblaue Verbindung die schwersten Partikel aufweist..
Beachten Sie, dass ein verallgemeinerter und übertriebener Trend angezeigt wird: Je höher die Molmasse ist, desto geringer ist die Probenmenge, die auf die Waage gelegt werden muss. Dieses Materievolumen hängt jedoch auch stark vom Aggregatzustand jeder Verbindung und ihrer Dichte ab..
Artikelverzeichnis
- 1 Wie berechnet man die Molmasse??
- 1.1 Definition
- 1.2 Elemente
- 1.3 Verbindungen
- 2 Beispiele
- 3 Gelöste Übungen
- 3.1 Übung 1
- 3.2 Übung 2
- 3.3 Übung 3
- 4 Referenzen
Wie berechnet man die Molmasse??

Definition
Die Molmasse kann anhand ihrer Definition berechnet werden: Massenmenge pro Mol Substanz:
M. = Gramm Substanz / Mol Substanz
Tatsächlich ist g / mol die Einheit, in der die Molmasse üblicherweise zusammen mit kg / mol ausgedrückt wird. Wenn wir also wissen, wie viele Mol wir von einer Verbindung oder einem Element haben, und wir es wiegen, werden wir durch Anwenden einer einfachen Division direkt zu ihrer Molmasse gelangen.
Elemente
Die Molmasse gilt nicht nur für Verbindungen, sondern auch für Elemente. Das Konzept der Maulwürfe unterscheidet überhaupt nicht. Mit Hilfe eines Periodensystems lokalisieren wir daher die relativen Atommassen für ein interessierendes Element und multiplizieren seinen Wert mit 1 g / mol; Dies ist die Konstante von Avogadro, M.ODER.
Zum Beispiel beträgt die relative Atommasse von Strontium 87,62. Wenn wir seine Atommasse haben wollen, wäre es 87,62 amu; Wenn wir aber nach seiner Molmasse suchen, dann sind es 87,62 g / mol (87,62 · 1 g / mol). Und so werden die Molmassen aller anderen Elemente auf die gleiche Weise erhalten, ohne dass diese Multiplikation überhaupt durchgeführt werden muss..
Verbindungen
Die Molmasse einer Verbindung ist nichts anderes als die Summe der relativen Atommassen ihrer Atome multipliziert mit M.ODER.
Zum Beispiel das Wassermolekül H.zweiOder es hat drei Atome: zwei Wasserstoff und einen Sauerstoff. Die relativen Atommassen von H und O betragen 1,008 bzw. 15,999. Wir addieren also ihre Massen, indem wir mit der Anzahl der im Molekül der Verbindung vorhandenen Atome multiplizieren:
2 H (1,008) = 2,016
1 O (15.999) = 15.999
M.(H.zweiO) = (2,016 + 15,999) 1 g / mol = 18,015 g / mol
Es ist eine ziemlich übliche Praxis, wegzulassen M.ODER schließlich:
M.(H.zweiO) = (2,016 + 15,999) = 18,015 g / mol
Unter Molmasse werden Einheiten von g / mol verstanden.
Beispiele
Eine der bekanntesten Molmassen wurde gerade erwähnt: die von Wasser, 18 g / mol. Diejenigen, die mit diesen Berechnungen vertraut sind, erreichen einen Punkt, an dem sie sich einige Molmassen merken können, ohne sie suchen oder berechnen zu müssen, wie oben beschrieben. Einige dieser Molmassen, die als Beispiele dienen, sind die folgenden:
-ODERzwei: 32 g / mol
-N.zwei: 28 g / mol
-NH3: 17 g / mol
-CH4: 16 g / mol
-COzwei: 44 g / mol
-HCl: 36,5 g / mol
-H.zweiSW4: 98 g / mol
-CH3COOH: 60 g / mol
-Fe: 56 g / mol
Beachten Sie, dass die angegebenen Werte gerundet sind. Für genauere Zwecke sollten die Molmassen auf Dezimalstellen ausgedrückt und mit den fälligen und genauen relativen Atommassen berechnet werden.
Gelöste Übungen
Übung 1
Durch analytische Verfahren wurde geschätzt, dass eine Lösung einer Probe 0,0267 Mol eines Analyten D enthält. Es ist auch bekannt, dass seine Masse 14% einer Probe entspricht, deren Gesamtmasse 76 Gramm beträgt. Berechnen Sie die Molmasse des mutmaßlichen Analyten D..
Wir müssen die Masse von D bestimmen, die in der Lösung gelöst ist. Wir fahren fort:
Masse (D) = 76 g 0,14 = 10,64 g D.
Das heißt, wir berechnen 14% der 76 Gramm der Probe, die den Gramm des Analyten D entsprechen. Dann wenden wir schließlich die Definition der Molmasse an, da wir über genügend Daten verfügen, um sie zu berechnen:
M.(D) = 10,64 g D / 0,0267 mol D.
= 398,50 g / mol
Was übersetzt bedeutet: ein Mol (6.022102. 3) von Y-Molekülen hat eine Masse von 398,50 Gramm. Dank dieses Wertes können wir wissen, wie viel Y wir auf der Waage wiegen möchten, wenn wir beispielsweise eine Lösung mit einer molaren Konzentration von 5 · 10 herstellen möchten-3 M; das heißt, 0,1993 g Y werden in einem Liter Lösungsmittel gelöst:
5 10-3 (mol / l) · (398,50 g / mol) = 0,1993 g Y.
Übung 2
Berechnen Sie die Molmasse der Zitronensäure in dem Wissen, dass ihre Molekülformel C ist6H.8ODER7.
Die gleiche Formel C.6H.8ODER7 Es erleichtert das Verständnis der Berechnung, da es uns sofort die Anzahl der C-, H- und O-Atome in Zitronensäure anzeigt. Daher wiederholen wir den gleichen Schritt, der für das Wasser ausgeführt wurde:
6 C · (12.0107) = 72.0642
8 H (1.008) = 8.064
7 O (15.999) = 111.993
M.(Zitronensäure) = 72,0642 + 8,064 + 111,993
= 192,1212 g / mol
Übung 3
Berechnen Sie die Molmasse von Kupfersulfatpentahydrat, CuSO45HzweiODER.
Wir wissen von früher, dass die Molmasse von Wasser 18,015 g / mol beträgt. Dies hilft uns, die Berechnungen zu vereinfachen, da wir sie momentan weglassen und uns auf das wasserfreie Salz CuSO konzentrieren4.
Wir haben, dass die relativen Atommassen von Kupfer und Schwefel 63,546 bzw. 32,065 betragen. Mit diesen Daten gehen wir genauso vor wie mit Übung 2:
1 Cu (63.546) = 63.546
1 S (32.065) = 32.065
4 O (15.999) = 63.996
M.(CuSO4) = 63.546 + 32.065 + 63.996
= 159,607 g / mol
Wir interessieren uns jedoch für die Molmasse des pentahydrierten Salzes, nicht für das wasserfreie. Dazu müssen wir dem Ergebnis die entsprechende Wassermasse hinzufügen:
5 hzweiO = 5 (18.015) = 90.075
M.(CuSO45HzweiO) = 159,607 + 90,075
= 249,682 g / mol
Verweise
- Whitten, Davis, Peck & Stanley. (2008). Chemie. (8. Aufl.). CENGAGE Lernen.
- Wikipedia. (2020). Molmasse. Wiederhergestellt von: en.wikipedia.org
- Nissa Garcia. (2020). Was ist Molmasse? Definition, Formel & Beispiele. Studie. Wiederhergestellt von: study.com
- Dr. Kristy M. Bailey. (s.f.). Stöchiometrie-Tutorial
Auffinden der Molmasse. Wiederhergestellt aus: occc.edu - Helmenstine, Anne Marie, Ph.D. (2. Dezember 2019). Beispiel für ein Molmassenproblem. Wiederhergestellt von :oughtco.com



Bisher hat noch niemand einen Kommentar zu diesem Artikel abgegeben.